- Кинематика как раздел физики
- Способы описания механического движения. Системы отсчёта
- знать объект изучения кинематики; понятия: механическое движение, система отсчёта, поступательное движение, материальная точка; три способа описания механического движения
- уметь приводить примеры поступательного движения; объяснять, в каком случае тело можно принять за точечное; выбирать систему отсчёта; определять достаточное количество осей для описания движения тела; определять координаты тела по графику
- Что такое система отсчёта?
- Почему движение тела нельзя описать без выбора системы отсчёта?
- Какие способы описания механического движения вы знаете?
Кинематика как раздел физики
Кинематика — это раздел механики, изучающий математическое описание механического движения тел, без рассмотрения причин этого движения.
Механическое движение — это изменение положения тела или частей этого тела в пространстве относительно других тел.
Кинематика позволяет определить, в какой точке пространства окажется тело в тот или иной момент времени.
Понятно, что все окружающие нас тела имеют конечные размеры. Если в условиях рассматриваемой задачи размерами тела можно пренебречь и рассматривать движение только одной его точки, такое тело называют точечным (материальной точкой).
Например, при заезде автомобиля в гараж нельзя пренебречь габаритами машины, но для описания движения того же автомобиля при его перемещении из одного города в другой — можно, так как расстояние между городами много больше размеров рассматриваемого тела.
Таким образом, размерами тела можно пренебречь в случае, если расстояние, пройденное данным телом, во много раз больше размеров самого тела.
Материальная точка (точечное тело) — это реальное физическое тело, геометрическими размерами которого в условиях данной задачи можно пренебречь.
Если реальное тело движется поступательно, его также можно заменить на материальную точку.
 Рис. 1. Поступательное движение кабины колеса обозрения
Рис. 1. Поступательное движение кабины колеса обозрения
Поступательное движение означает, что все точки рассматриваемого тела имеют одинаковые векторы скорости в любой момент времени. То есть любая точка тела движется с одинаковой по модулю скоростью и в одном и том же направлении.
Например, кабина колеса обозрения движется поступательно: несмотря на то что тело движется по окружности, все точки, принадлежащие данному телу, движутся в одном направлении и с одинаковыми скоростями (рис. 1). В данном случае для описания характера движения кабины достаточно описать движение одной её точки, поэтому кабину колеса обозрения можно принять за точечное тело.
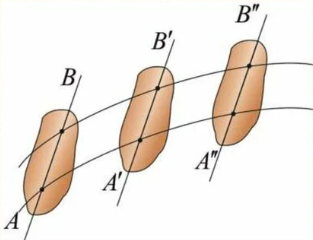 Рис. 2. АВ//А’B’//A’’B’’
Рис. 2. АВ//А’B’//A’’B’’
Понятно, что если все точки рассматриваемого тела имеют одинаковые направления и модули скорости, то прямая, проведённая через любые две точки этого тела, при движении данного тела в любой момент времени будет оставаться параллельна своему исходному положению (рис. 2).
Поступательным называют такое движение тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
Прямолинейное движение — это один из видов поступательного движения, когда тело двигается вдоль заданной прямой.
Способы описания механического движения. Системы отсчёта
Характер движения тела зависит от выбранной системы отсчёта. Например, когда вы едете в автобусе по дороге в школу, относительно земли ваша скорость равна скорости автобуса; относительно автобуса ваша скорость равна нулю. Поэтому описание движения материальной точки невозможно без выбора системы отсчёта.
При изучении прямолинейного движения в 7 классе мы использовали следующее определение системы отсчёта.
Система отсчета — совокупность тела отсчёта, системы координат и прибора для измерения времени.
Рассмотрим пример выбора системы отсчёта и описания движения точечного тела в выбранной системе отсчёта.
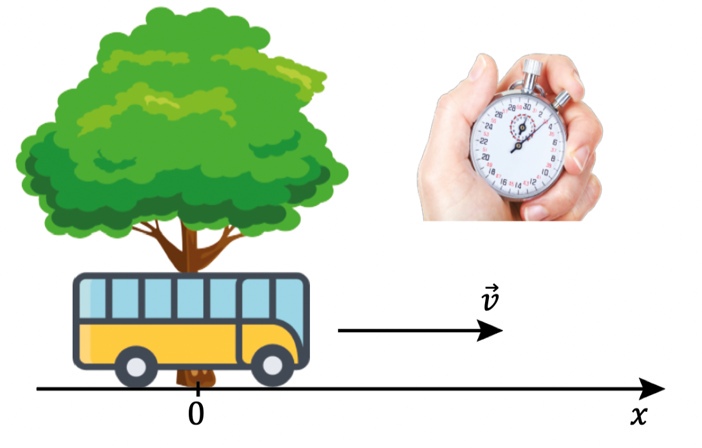 Рис. 3. Положение автобуса в начальный момент времени в системе отсчёта, связанной с деревом
Рис. 3. Положение автобуса в начальный момент времени в системе отсчёта, связанной с деревом
Пусть автобус движется с постоянной скоростью по прямолинейной дороге. Будем рассматривать механическое движение автобуса относительно неподвижного дерева, иными словами, дерево — это тело отсчёта. В место, где располагается дерево, поместим начало системы координат. В нашем случае это только ось X, так как автобус движется в одном направлении.
Момент времени, когда автобус поравняется с деревом, мы будем считать начальным: t = 0. В этот момент включается прибор для измерения времени — секундомер — и начинаются наблюдения (рис. 3).
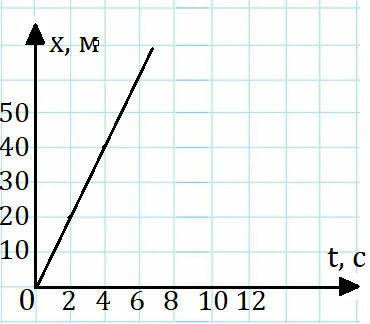 Рис. 4. Графический способ описания движения
Рис. 4. Графический способ описания движения
В момент, когда начинается наблюдение, начальная координата автобуса x0 = 0. Результаты изменения координаты с течением времени можно представить тремя способами: в табличной форме, в форме графика движения (рис. 4) или в виде аналитической зависимости координаты от времени: x = 10t.
Если задана графическая или аналитическая зависимость координаты тела от времени при прямолинейном движении данного тела, то всегда можно определить координату тела в любой момент времени, а также найти значение времени, через которое тело окажется в заданной координате.
В этом случае говорят, что движение тела в выбранной системе отсчёта полностью описано.
Понятно, что не все тела движутся прямолинейно: автобус может свернуть на прилегающую дорогу. Тогда линия, вдоль которой перемещается автобус (траектория) не будет иметь форму прямой.
Линия, вдоль которой движется тело, называется траекторией.
Если форма траектории материальной точки имеет форму кривой линии, такое движение называется криволинейным. Частным случаем криволинейного движения является движение по окружности.
Для описания криволинейного движения в плоскости используются две оси: ОX и OY соответственно. Положение точечного тела будет задаваться двумя координатами x и y.
Оси должны быть связаны с телом отсчёта так, чтобы они располагались в плоскости движения тела и пересекали начало отсчёта.
Направления координатных осей выбираются, исходя из удобства решения конкретной задачи.
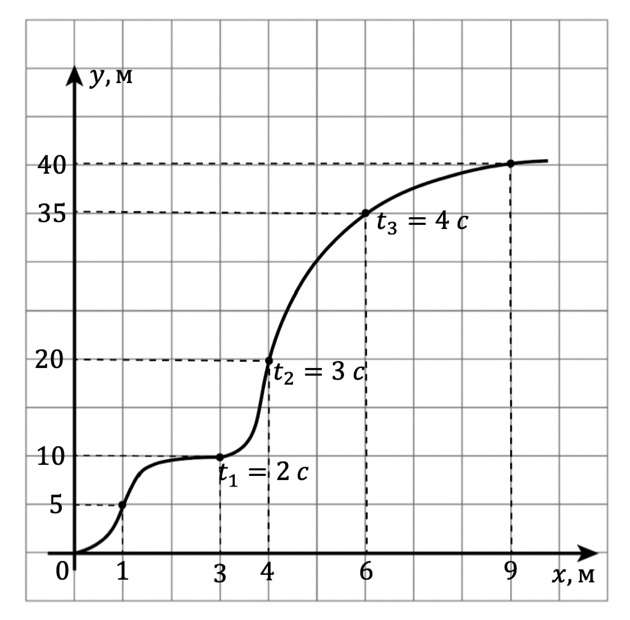 Рис. 5. Изменение координат x и y с течением времени
Рис. 5. Изменение координат x и y с течением времени
На рисунке 5 приведён пример описания криволинейного движения жука по земле с помощью двух осей координат. Жук движется в одной плоскости — плоскости поверхности земли.
Телом отсчёта в данной системе является земля. Точки на графике отмечены через равные промежутки времени — 1 с.
В начальный момент времени t0 = 0 жук находится в точке с координатами x0 = 0 м , y0 = 0 м.
Для определения координат точки по графику необходимо из данной точки опустить перпендикуляры на оси ОХ и OY, полученные значения будут соответствовать координатам x и y.
Таким образом, в момент времени t1 = 2 c жук находится в точке с координатами
x1 = 3 м, y1 = 10 м; в момент времени t2 = 3 c — в точке с координатами x2 = 4 м,
y2 = 20 м и так далее.
Подчеркнём, что при криволинейном движении тела в некоторой плоскости, необходимо задавать два закона движения: x(t) — зависимость координаты x от времени t; y(t) — зависимость координаты y от времени t.
Если тело движется в пространстве, то для однозначного описания движения такого тела необходимо использовать трёхмерную систему координат: совокупность осей OX, OY, OZ и начала отсчёта.
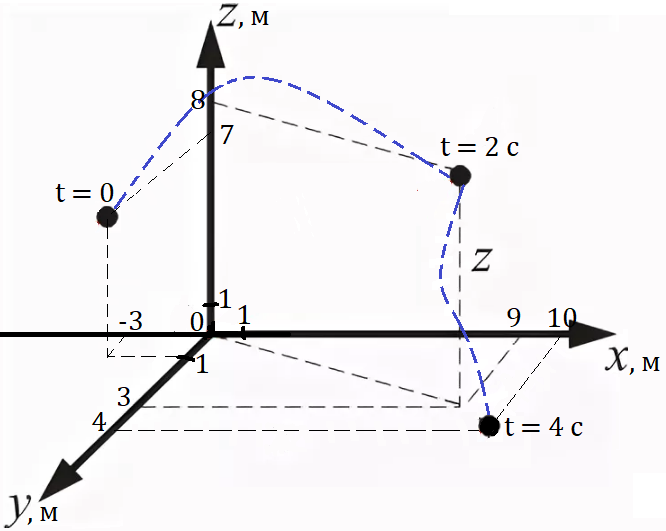 Рис. 6. Система отсчёта для описания движения тела в нескольких плоскостях
Рис. 6. Система отсчёта для описания движения тела в нескольких плоскостях
Например, бабочка во время полёта перемещается в трёх направлениях относительно начала отсчёта (рис. 6). Примем за тело отсчёта поверхность земли, а в качестве начала отсчёта — точки с координатами x = 0; y = 0; z = 0 — цветок на поляне.
Положение бабочки в каждый момент времени определяется тремя координатами x, y, z. Точки отмечены через равные промежутки времени t = 2 c. Синими цветом показана траектория движения бабочки в пространстве.
В начальный момент времени t0 = 0 бабочка находится в точке с координатами
x0 = −3 м, y0 = 1 м, z0 = 7 м.
Через две секунды в момент времени t1 = 2 с бабочка уже находится в точке с координатами x1 = 9 м, y1 = 3 м, z1 = 8 м. Ещё через две секунды — в точке с координатами x2 = 10 м, y2 = 4 м, z2 = 0 м — бабочка приземлилась на землю.
Понятно, что для описания такого сложного вида движения необходимо задавать три закона движения, три зависимости координаты от времени: xt;yt;z(t). Приведём графическое описание изменения координат бабочки с течением времени в системе отсчёта, связанной с землёй (рис. 7).
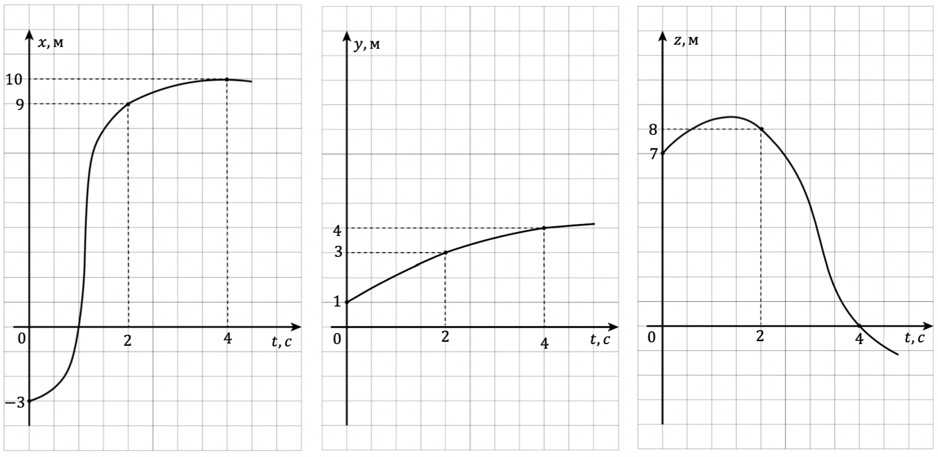 Рис. 7. Изменение координат x, y, z с течением времени в системе отсчёта, связанной с землёй
Рис. 7. Изменение координат x, y, z с течением времени в системе отсчёта, связанной с землёй
Итоги
- Кинематика — это раздел механики, изучающий математическое описание механического движения тел без рассмотрения причин этого движения.
- Материальная точка (точечное тело) — это реальное физическое тело, геометрическими размерами которого в условиях данной задачи можно пренебречь.
- Система отсчёта — совокупность тела отсчёта, системы координат и прибора для измерения времени.
- Поступательным называют такое движение тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
- Механическое движение тела можно описать тремя способами: табличным способом, графическим или аналитическим.
Контрольные вопросы
1. Приведите пример поступательного движения.
2. Назовите три способа описания движения.
3. Сколько координатных осей потребуется для описания движения грузовика; птицы; молекулы газообразного вещества?
- Кинематика как раздел физики
- Способы описания механического движения. Системы отсчёта
- знать объект изучения кинематики; понятия: механическое движение, система отсчёта, поступательное движение, материальная точка; три способа описания механического движения
- уметь приводить примеры поступательного движения; объяснять, в каком случае тело можно принять за точечное; выбирать систему отсчёта; определять достаточное количество осей для описания движения тела; определять координаты тела по графику
- Что такое система отсчёта?
- Почему движение тела нельзя описать без выбора системы отсчёта?
- Какие способы описания механического движения вы знаете?
Кинематика как раздел физики
Кинематика — это раздел механики, изучающий математическое описание механического движения тел, без рассмотрения причин этого движения.
Механическое движение — это изменение положения тела или частей этого тела в пространстве относительно других тел.
Кинематика позволяет определить, в какой точке пространства окажется тело в тот или иной момент времени.
Понятно, что все окружающие нас тела имеют конечные размеры. Если в условиях рассматриваемой задачи размерами тела можно пренебречь и рассматривать движение только одной его точки, такое тело называют точечным (материальной точкой).
Например, при заезде автомобиля в гараж нельзя пренебречь габаритами машины, но для описания движения того же автомобиля при его перемещении из одного города в другой — можно, так как расстояние между городами много больше размеров рассматриваемого тела.
Таким образом, размерами тела можно пренебречь в случае, если расстояние, пройденное данным телом, во много раз больше размеров самого тела.
Материальная точка (точечное тело) — это реальное физическое тело, геометрическими размерами которого в условиях данной задачи можно пренебречь.
Если реальное тело движется поступательно, его также можно заменить на материальную точку.
 Рис. 1. Поступательное движение кабины колеса обозрения
Рис. 1. Поступательное движение кабины колеса обозрения
Поступательное движение означает, что все точки рассматриваемого тела имеют одинаковые векторы скорости в любой момент времени. То есть любая точка тела движется с одинаковой по модулю скоростью и в одном и том же направлении.
Например, кабина колеса обозрения движется поступательно: несмотря на то что тело движется по окружности, все точки, принадлежащие данному телу, движутся в одном направлении и с одинаковыми скоростями (рис. 1). В данном случае для описания характера движения кабины достаточно описать движение одной её точки, поэтому кабину колеса обозрения можно принять за точечное тело.
 Рис. 2. АВ//А’B’//A’’B’’
Рис. 2. АВ//А’B’//A’’B’’
Понятно, что если все точки рассматриваемого тела имеют одинаковые направления и модули скорости, то прямая, проведённая через любые две точки этого тела, при движении данного тела в любой момент времени будет оставаться параллельна своему исходному положению (рис. 2).
Поступательным называют такое движение тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
Прямолинейное движение — это один из видов поступательного движения, когда тело двигается вдоль заданной прямой.
Способы описания механического движения. Системы отсчёта
Характер движения тела зависит от выбранной системы отсчёта. Например, когда вы едете в автобусе по дороге в школу, относительно земли ваша скорость равна скорости автобуса; относительно автобуса ваша скорость равна нулю. Поэтому описание движения материальной точки невозможно без выбора системы отсчёта.
При изучении прямолинейного движения в 7 классе мы использовали следующее определение системы отсчёта.
Система отсчета — совокупность тела отсчёта, системы координат и прибора для измерения времени.
Рассмотрим пример выбора системы отсчёта и описания движения точечного тела в выбранной системе отсчёта.
 Рис. 3. Положение автобуса в начальный момент времени в системе отсчёта, связанной с деревом
Рис. 3. Положение автобуса в начальный момент времени в системе отсчёта, связанной с деревом
Пусть автобус движется с постоянной скоростью по прямолинейной дороге. Будем рассматривать механическое движение автобуса относительно неподвижного дерева, иными словами, дерево — это тело отсчёта. В место, где располагается дерево, поместим начало системы координат. В нашем случае это только ось X, так как автобус движется в одном направлении.
Момент времени, когда автобус поравняется с деревом, мы будем считать начальным: t = 0. В этот момент включается прибор для измерения времени — секундомер — и начинаются наблюдения (рис. 3).
 Рис. 4. Графический способ описания движения
Рис. 4. Графический способ описания движения
В момент, когда начинается наблюдение, начальная координата автобуса x0 = 0. Результаты изменения координаты с течением времени можно представить тремя способами: в табличной форме, в форме графика движения (рис. 4) или в виде аналитической зависимости координаты от времени: x = 10t.
Если задана графическая или аналитическая зависимость координаты тела от времени при прямолинейном движении данного тела, то всегда можно определить координату тела в любой момент времени, а также найти значение времени, через которое тело окажется в заданной координате.
В этом случае говорят, что движение тела в выбранной системе отсчёта полностью описано.
Понятно, что не все тела движутся прямолинейно: автобус может свернуть на прилегающую дорогу. Тогда линия, вдоль которой перемещается автобус (траектория) не будет иметь форму прямой.
Линия, вдоль которой движется тело, называется траекторией.
Если форма траектории материальной точки имеет форму кривой линии, такое движение называется криволинейным. Частным случаем криволинейного движения является движение по окружности.
Для описания криволинейного движения в плоскости используются две оси: ОX и OY соответственно. Положение точечного тела будет задаваться двумя координатами x и y.
Оси должны быть связаны с телом отсчёта так, чтобы они располагались в плоскости движения тела и пересекали начало отсчёта.
Направления координатных осей выбираются, исходя из удобства решения конкретной задачи.
 Рис. 5. Изменение координат x и y с течением времени
Рис. 5. Изменение координат x и y с течением времени
На рисунке 5 приведён пример описания криволинейного движения жука по земле с помощью двух осей координат. Жук движется в одной плоскости — плоскости поверхности земли.
Телом отсчёта в данной системе является земля. Точки на графике отмечены через равные промежутки времени — 1 с.
В начальный момент времени t0 = 0 жук находится в точке с координатами x0 = 0 м , y0 = 0 м.
Для определения координат точки по графику необходимо из данной точки опустить перпендикуляры на оси ОХ и OY, полученные значения будут соответствовать координатам x и y.
Таким образом, в момент времени t1 = 2 c жук находится в точке с координатами
x1 = 3 м, y1 = 10 м; в момент времени t2 = 3 c — в точке с координатами x2 = 4 м,
y2 = 20 м и так далее.
Подчеркнём, что при криволинейном движении тела в некоторой плоскости, необходимо задавать два закона движения: x(t) — зависимость координаты x от времени t; y(t) — зависимость координаты y от времени t.
Если тело движется в пространстве, то для однозначного описания движения такого тела необходимо использовать трёхмерную систему координат: совокупность осей OX, OY, OZ и начала отсчёта.
 Рис. 6. Система отсчёта для описания движения тела в нескольких плоскостях
Рис. 6. Система отсчёта для описания движения тела в нескольких плоскостях
Например, бабочка во время полёта перемещается в трёх направлениях относительно начала отсчёта (рис. 6). Примем за тело отсчёта поверхность земли, а в качестве начала отсчёта — точки с координатами x = 0; y = 0; z = 0 — цветок на поляне.
Положение бабочки в каждый момент времени определяется тремя координатами x, y, z. Точки отмечены через равные промежутки времени t = 2 c. Синими цветом показана траектория движения бабочки в пространстве.
В начальный момент времени t0 = 0 бабочка находится в точке с координатами
x0 = −3 м, y0 = 1 м, z0 = 7 м.
Через две секунды в момент времени t1 = 2 с бабочка уже находится в точке с координатами x1 = 9 м, y1 = 3 м, z1 = 8 м. Ещё через две секунды — в точке с координатами x2 = 10 м, y2 = 4 м, z2 = 0 м — бабочка приземлилась на землю.
Понятно, что для описания такого сложного вида движения необходимо задавать три закона движения, три зависимости координаты от времени: xt;yt;z(t). Приведём графическое описание изменения координат бабочки с течением времени в системе отсчёта, связанной с землёй (рис. 7).
 Рис. 7. Изменение координат x, y, z с течением времени в системе отсчёта, связанной с землёй
Рис. 7. Изменение координат x, y, z с течением времени в системе отсчёта, связанной с землёй
Итоги
- Кинематика — это раздел механики, изучающий математическое описание механического движения тел без рассмотрения причин этого движения.
- Материальная точка (точечное тело) — это реальное физическое тело, геометрическими размерами которого в условиях данной задачи можно пренебречь.
- Система отсчёта — совокупность тела отсчёта, системы координат и прибора для измерения времени.
- Поступательным называют такое движение тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
- Механическое движение тела можно описать тремя способами: табличным способом, графическим или аналитическим.
Контрольные вопросы
1. Приведите пример поступательного движения.
2. Назовите три способа описания движения.
3. Сколько координатных осей потребуется для описания движения грузовика; птицы; молекулы газообразного вещества?



