- Формулы объёмов;
- Примеры задач на комбинации тел.
- Уметь применять формулы объёмов;
- Уметь решать задачи на комбинации тел.
- Объёмы каких тел – это произведение площади основания на высоту?
- Во сколько раз изменится объём тетраэдра, если длины всех его ребер уменьшить в два раза?
- Чему равен объём тела, ограниченного полусферой?
Задачи на комбинации тел
Вспомним формулы объёмов многогранников и тел вращения.
Объём призмы с высотой можно вычислить по формуле:
.
Формула для нахождения объёма пирамиды с высотой имеет вид:
.
Формулы для нахождения объёма цилиндра и конуса очень похожи на предыдущие. Но если принять во внимание, что основанием цилиндра и конуса всегда является круг радиуса с площадью , то объёмы этих тел вращения можно вычислить по формулам: и соответственно, где - высота цилиндра или конуса.
Объём шара радиуса можно вычислить по формуле:
.
Пример 1
В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9 (рис. 1). Боковые рёбра призмы равны 8. Найдите объём цилиндра, описанного около этой призмы.
Решение
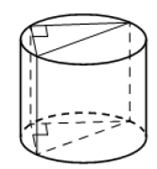 Рис. 1. Прямая призма вписана в цилиндр
Рис. 1. Прямая призма вписана в цилиндр
Объём цилиндра с радиусом основания можно вычислить по формуле
Так как призма прямая, то её высота равна длине бокового ребра, следовательно, высота цилиндра также равна 8.
Чтобы найти радиус основания, необходимо найти длину гипотезы (если прямоугольный треугольник вписан в окружность, то гипотенуза этого треугольника является диаметром). По теореме Пифагора гипотенуза равна:
.
Тогда
,
где – диаметр основания.
Подставим все найденные значения в формулу объёма цилиндра и вычислим:
.
Ответ: .
Упражнение 1
1. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны 6. Найдите объем цилиндра, описанного около этой призмы.
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6,5. Найдите объем параллелепипеда.
Пример 2
Шар вписан в цилиндр (рис. 2). Площадь поверхности цилиндра равна . Найдите объём шара.
Решение
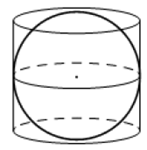 Рис. 2. Шар вписан в цилиндр
Рис. 2. Шар вписан в цилиндр
Объём шара можно вычислить по формуле .
Найдем радиус шара. Так как шар вписан в цилиндр, то радиус шара равен радиусу основания цилиндра, а высота цилиндра равна диаметру шара, т.е. .
Выразим радиус через формулу площади поверхности цилиндра:
.
.
.
Подставим значение радиуса в формулу объёма шара и вычислим его значение:
.
Ответ: .
Упражнение 2
1. Шар, объём которого равен 72, вписан в цилиндр. Найдите объём цилиндра.
2. В куб с ребром 6 вписан шар. Найдите объём этого шара.
Пример 3
Конус, высота которого равна радиусу основания, вписан в правильную четырехугольную пирамиду, объём которой равен 36. Найдите объём конуса.
Решение
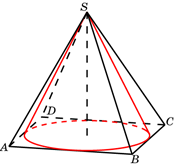 Рис. 3. Конус вписан в четырехугольную пирамиду
Рис. 3. Конус вписан в четырехугольную пирамиду
Выразим объём конуса через радиус:
.
Основанием правильной пирамиды является квадрат, в который вписан круг (основание конуса). Значит, сторона основания пирамиды равна диаметру основания конуса, т.е. . Тогда площадь основания пирамиды равна .
Высоты пирамиды и конуса совпадают, значит, высота пирамиды тоже равна .
Тогда формула объёма пирамиды примет вид:
,
откуда
.
Теперь можем найти объём конуса:
.
Ответ: .
Упражнение 3
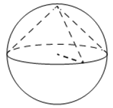 Рис. 4. Конус, вписанный в шар
Рис. 4. Конус, вписанный в шар
1. Конус, высота которого равна радиусу основания, вписан в правильную треугольную пирамиду, объём которой равен . Найдите объём конуса.
2. Конус вписан в шар (рис. 4). Радиус основания конуса равен радиусу шара. Объём конуса равен 13. Найдите объём шара.
Контрольные вопросы
1. В какую четырехугольную призму можно вписать шар? Почему?
2. В треугольную правильную пирамиду вписан конус с радиусом основания и высотой . Чему равны высота и сторона основания пирамиды?
Упражнение 1
1. .
2. .
Упражнение 2
1. .
2. .
Упражнение 3
1. .
2. .
- Формулы объёмов;
- Примеры задач на комбинации тел.
- Уметь применять формулы объёмов;
- Уметь решать задачи на комбинации тел.
- Объёмы каких тел – это произведение площади основания на высоту?
- Во сколько раз изменится объём тетраэдра, если длины всех его ребер уменьшить в два раза?
- Чему равен объём тела, ограниченного полусферой?
Задачи на комбинации тел
Вспомним формулы объёмов многогранников и тел вращения.
Объём призмы с высотой можно вычислить по формуле:
.
Формула для нахождения объёма пирамиды с высотой имеет вид:
.
Формулы для нахождения объёма цилиндра и конуса очень похожи на предыдущие. Но если принять во внимание, что основанием цилиндра и конуса всегда является круг радиуса с площадью , то объёмы этих тел вращения можно вычислить по формулам: и соответственно, где - высота цилиндра или конуса.
Объём шара радиуса можно вычислить по формуле:
.
Пример 1
В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9 (рис. 1). Боковые рёбра призмы равны 8. Найдите объём цилиндра, описанного около этой призмы.
Решение
 Рис. 1. Прямая призма вписана в цилиндр
Рис. 1. Прямая призма вписана в цилиндр
Объём цилиндра с радиусом основания можно вычислить по формуле
Так как призма прямая, то её высота равна длине бокового ребра, следовательно, высота цилиндра также равна 8.
Чтобы найти радиус основания, необходимо найти длину гипотезы (если прямоугольный треугольник вписан в окружность, то гипотенуза этого треугольника является диаметром). По теореме Пифагора гипотенуза равна:
.
Тогда
,
где – диаметр основания.
Подставим все найденные значения в формулу объёма цилиндра и вычислим:
.
Ответ: .
Упражнение 1
1. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. Боковые ребра равны 6. Найдите объем цилиндра, описанного около этой призмы.
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6,5. Найдите объем параллелепипеда.
Пример 2
Шар вписан в цилиндр (рис. 2). Площадь поверхности цилиндра равна . Найдите объём шара.
Решение
 Рис. 2. Шар вписан в цилиндр
Рис. 2. Шар вписан в цилиндр
Объём шара можно вычислить по формуле .
Найдем радиус шара. Так как шар вписан в цилиндр, то радиус шара равен радиусу основания цилиндра, а высота цилиндра равна диаметру шара, т.е. .
Выразим радиус через формулу площади поверхности цилиндра:
.
.
.
Подставим значение радиуса в формулу объёма шара и вычислим его значение:
.
Ответ: .
Упражнение 2
1. Шар, объём которого равен 72, вписан в цилиндр. Найдите объём цилиндра.
2. В куб с ребром 6 вписан шар. Найдите объём этого шара.
Пример 3
Конус, высота которого равна радиусу основания, вписан в правильную четырехугольную пирамиду, объём которой равен 36. Найдите объём конуса.
Решение
 Рис. 3. Конус вписан в четырехугольную пирамиду
Рис. 3. Конус вписан в четырехугольную пирамиду
Выразим объём конуса через радиус:
.
Основанием правильной пирамиды является квадрат, в который вписан круг (основание конуса). Значит, сторона основания пирамиды равна диаметру основания конуса, т.е. . Тогда площадь основания пирамиды равна .
Высоты пирамиды и конуса совпадают, значит, высота пирамиды тоже равна .
Тогда формула объёма пирамиды примет вид:
,
откуда
.
Теперь можем найти объём конуса:
.
Ответ: .
Упражнение 3
 Рис. 4. Конус, вписанный в шар
Рис. 4. Конус, вписанный в шар
1. Конус, высота которого равна радиусу основания, вписан в правильную треугольную пирамиду, объём которой равен . Найдите объём конуса.
2. Конус вписан в шар (рис. 4). Радиус основания конуса равен радиусу шара. Объём конуса равен 13. Найдите объём шара.
Контрольные вопросы
1. В какую четырехугольную призму можно вписать шар? Почему?
2. В треугольную правильную пирамиду вписан конус с радиусом основания и высотой . Чему равны высота и сторона основания пирамиды?
Упражнение 1
1. .
2. .
Упражнение 2
1. .
2. .
Упражнение 3
1. .
2. .
