- Сфера и многогранник;
- Цилиндр и призма;
- Цилиндр и пирамида;
- Конус и призма;
- Конус и пирамида;
- Конус и цилиндр.
- Знать, что представляет собой сфера (шар), описанная около многогранника;
- Знать, что представляет собой сфера (шар), вписанная в многогранник;
- Знать, что представляет собой тело вращения, описанное около многогранника (примеры);
- Знать, что представляет собой тело вращения, вписанное в многогранник (примеры);
- Уметь решать задачи на комбинации различных геометрических тел.
- Какая окружность называется вписанной в многоугольник?
- Какая окружность называется описанной около многоугольника?
В жизни мы часто встречаемся с такими объектами, которые невозможно описать с помощью какой-то одной фигуры. Поэтому возникает необходимость рассмотрения комбинации различных фигур. С этим мы сталкивались и в курсе планиметрии. Рассмотрим теперь наиболее важные комбинации различных геометрических тел в пространстве.
Сфера и многогранник
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере (рис. 1).
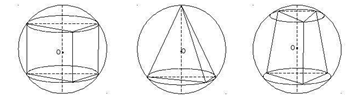 Рис. 1. Примеры сфер, описанных около многогранника
Рис. 1. Примеры сфер, описанных около многогранника
Из определения следует, что центр описанной сферы равноудалён от всех вершин многогранника.
Сфера (шар) называется вписанным в многогранник, если сфера касается всех граней многогранника (рис. 2).
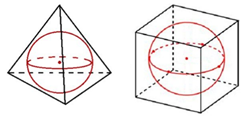 Рис. 2. Примеры сфер, вписанных в многогранник
Рис. 2. Примеры сфер, вписанных в многогранник
Центр вписанной сферы равноудалён от всех граней многогранника.
Как известно, не вокруг любого многоугольника можно описать окружность и не в любой многоугольник можно вписать окружность.
Аналогично, не вокруг любого многогранника можно описать шар и не в любой многогранник можно вписать шар.
Пример 1
Доказать, что вокруг правильной пирамиды можно описать шар и центр этого шара лежит на ее высоте.
Доказательство
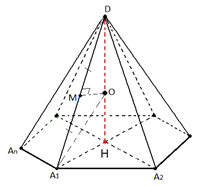 Рис. 3.
Рис. 3.
Рассмотрим правильную пирамиду (рис. 3).
Проведём высоту . Прямая является осью данной правильной пирамиды. Любая точка этой оси равноудалена от вершин основания. Отметим на боковом ребре середину M и в плоскости через точку проведём прямую, перпендикулярную к прямой . Эта прямая пересечёт ось пирамиды в некоторой точке . В треугольнике отрезок является медианой и высотой. Следовательно, треугольник равнобедренный (). Таким образом, точка , лежащая на оси пирамиды равноудалена от всех вершин этой пирамиды. Причём такая точка – единственная. Значит найденная точка, лежащая на оси пирамиды, является центром шара, описанного около данной пирамиды.
Что и требовалось доказать.
Пример 2
Доказать, что в правильную пирамиду можно вписать шар и центр этого шара лежит на ее высоте.
Доказательство
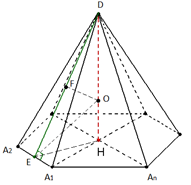 Рис. 4.
Рис. 4.
Рассмотрим правильную пирамиду (рис. 4).
Проведём высоту . Прямая является осью данной правильной пирамиды. Любая точка этой оси равноудалена от боковых граней этой пирамиды. Проведём апофему грани . Биссектриса угла пересекает высоту пирамиды в некоторой точке . По свойству биссектрисы точка равноудалена от сторон угла ( и ), а значит расстояния от точки до боковой грани и до основания одинаковы. Таким образом, точка , лежащая на высоте, равноудалена от всех граней данной пирамиды. Причём такая точка единственная, а значит является центром вписанного шара.
Что и требовалось доказать.
Пример 3
Найдите радиус шара, описанного около правильного тетраэдра с ребром .
Решение
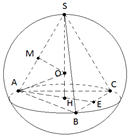 Рис. 5.
Рис. 5.
Дан правильный тетраэдр с ребром , вокруг которого описан шар (рис. 5).
Пусть – высота тетраэдра. Тогда точка является центром описанной вокруг треугольника окружности. Проведём высоту треугольника . Так как треугольник правильный, то является также медианой и биссектрисой этого треугольника.
.
Точка является центром треугольника и делит отрезок в отношении 2:1.
, .
Проведём из центра шара перпендикуляр к боковому ребру . Так как треугольник равнобедренный с основанием , то является медианой этого треугольника. Поэтому .
Треугольники и подобны, так как (прямые), (общий угол).
Из подобия треугольников и следует .
.
Ответ: .
Цилиндр и призма
Цилиндр вписан в призму, если основания цилиндра вписаны в основания призмы (рис. 6).
Цилиндр описан около призмы, если его основания описаны около оснований призмы (рис. 7).
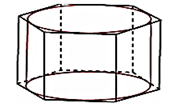 Рис. 6.
Рис. 6.
Из определения цилиндра, вписанного в призму, следует, что цилиндр можно вписать в призму только в том случае, если можно в основание призмы вписать окружность.
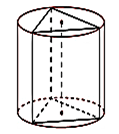 Рис. 7.
Рис. 7.
То же самое касается и цилиндра, описанного около призмы. Около призмы можно описать цилиндр лишь в том случае, если можно описать окружность вокруг основания призмы.
Известно, что в любой треугольник можно вписать окружность и вокруг любого треугольника можно описать окружность. Это означает, что в любую треугольную призму можно вписать цилиндр и вокруг любой треугольной призмы можно описать цилиндр.
Пример 4
Цилиндр описан около правильной шестиугольной призмы. Найдите угол между диагональю её боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Решение
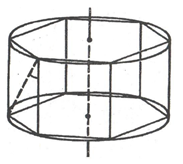 Рис. 8.
Рис. 8.
Из условия задачи следует, что боковые грани призмы – квадраты, так как сторона шестиугольника, вписанного в окружность, равна радиусу (рис. 8). Рёбра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А угол между диагональю и стороной квадрата равен .
Ответ: .
Цилиндр и пирамида
Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной её основанию (рис. 9).
Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра (рис. 10).
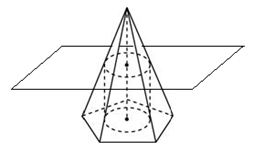 Рис. 9.
Рис. 9.
Очевидно, что высота вписанного в пирамиду цилиндра меньше высоты пирамиды. Если же цилиндр описан около пирамиды, то высота цилиндра равна высоте пирамиды.
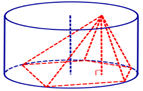 Рис. 10.
Рис. 10.
Из определений также следует, что если пирамида правильная, то в неё можно вписать цилиндр и около неё можно описать цилиндр.
Конус и призма
Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы (рис. 11).
Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса (рис. 12).
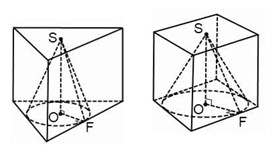 Рис. 11.
Рис. 11.
Вписать конус можно только в такую призму, в основание которой можно вписать окружность.
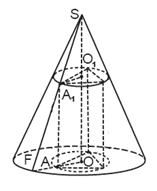 Рис. 12.
Рис. 12.
Если конус вписан в прямую призму, часть сечения комбинации тел плоскостью, проходящей через ось конуса, представляет собой прямоугольный треугольник, катеты которого — высота конуса (и призмы) и радиус конуса (и вписанной в основание призмы окружности), а гипотенуза — образующая конуса.
Высота конуса, описанного около призмы больше высоты призмы. Если же конус вписан в призму, то высота конуса равна высоте призмы.
Конус и пирамида
Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды (рис. 13).
Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды (рис. 14).
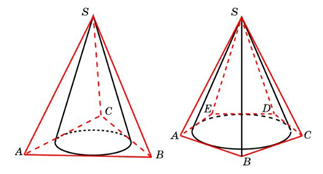 Рис. 13.
Рис. 13.
Конус можно вписать в пирамиду только в том случае, если можно в основание пирамиды вписать окружность.
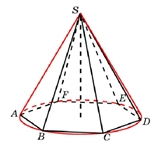 Рис. 14.
Рис. 14.
Аналогично, около пирамиды можно описать конус лишь в том случае, если можно описать окружность вокруг основания пирамиды.
При этом как в случае вписанного в пирамиду конуса, так и в случае описанного около пирамиды конуса, высоты конуса и пирамиды совпадают.
Конус и цилиндр
Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра (рис. 15).
Конус описан около цилиндра, если одно из оснований цилиндра касается поверхности конуса, а другое его основание принадлежит основанию конуса (рис. 16).
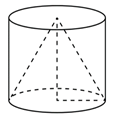 Рис. 15.
Рис. 15.
Очевидно, что в любой цилиндр можно вписать конус.
Оси цилиндра и вписанного в него конуса совпадают. Цилиндр и вписанный конус имеют равные высоты и радиусы.
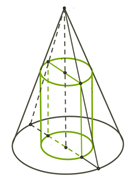 Рис. 16.
Рис. 16.
В любой конус можно вписать бесконечное множество цилиндров (радиусы цилиндров меньше радиуса конуса).
Центры оснований конуса и цилиндра совпадают, а высоты и радиусы различаются.
Упражнение
- Найдите радиус шара, описанного около куба с ребром .
- Докажите, что если в правильную призму можно вписать сферу, то центром сферы является середина отрезка, соединяющего центры оснований этой призмы.
- В правильную шестиугольную призму вписан шар радиуса 1. Найдите сторону основания и высоту призмы.
- Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 2.
Контрольные вопросы
- Какую сферу называют описанной около многогранника?
- Какую сферу называют вписанной в многогранник?
- Можно ли вокруг правильной пирамиды описать шар?
- Можно ли в правильную пирамиду вписать шар?
- Приведите примеры комбинации геометрических тел. Сделайте схематические рисунки.
Упражнение
1. .
3. , .
4. .
- Сфера и многогранник;
- Цилиндр и призма;
- Цилиндр и пирамида;
- Конус и призма;
- Конус и пирамида;
- Конус и цилиндр.
- Знать, что представляет собой сфера (шар), описанная около многогранника;
- Знать, что представляет собой сфера (шар), вписанная в многогранник;
- Знать, что представляет собой тело вращения, описанное около многогранника (примеры);
- Знать, что представляет собой тело вращения, вписанное в многогранник (примеры);
- Уметь решать задачи на комбинации различных геометрических тел.
- Какая окружность называется вписанной в многоугольник?
- Какая окружность называется описанной около многоугольника?
В жизни мы часто встречаемся с такими объектами, которые невозможно описать с помощью какой-то одной фигуры. Поэтому возникает необходимость рассмотрения комбинации различных фигур. С этим мы сталкивались и в курсе планиметрии. Рассмотрим теперь наиболее важные комбинации различных геометрических тел в пространстве.
Сфера и многогранник
Сфера (шар) называется описанной около многогранника, если все вершины многогранника лежат на сфере (рис. 1).
 Рис. 1. Примеры сфер, описанных около многогранника
Рис. 1. Примеры сфер, описанных около многогранника
Из определения следует, что центр описанной сферы равноудалён от всех вершин многогранника.
Сфера (шар) называется вписанным в многогранник, если сфера касается всех граней многогранника (рис. 2).
 Рис. 2. Примеры сфер, вписанных в многогранник
Рис. 2. Примеры сфер, вписанных в многогранник
Центр вписанной сферы равноудалён от всех граней многогранника.
Как известно, не вокруг любого многоугольника можно описать окружность и не в любой многоугольник можно вписать окружность.
Аналогично, не вокруг любого многогранника можно описать шар и не в любой многогранник можно вписать шар.
Пример 1
Доказать, что вокруг правильной пирамиды можно описать шар и центр этого шара лежит на ее высоте.
Доказательство
 Рис. 3.
Рис. 3.
Рассмотрим правильную пирамиду (рис. 3).
Проведём высоту . Прямая является осью данной правильной пирамиды. Любая точка этой оси равноудалена от вершин основания. Отметим на боковом ребре середину M и в плоскости через точку проведём прямую, перпендикулярную к прямой . Эта прямая пересечёт ось пирамиды в некоторой точке . В треугольнике отрезок является медианой и высотой. Следовательно, треугольник равнобедренный (). Таким образом, точка , лежащая на оси пирамиды равноудалена от всех вершин этой пирамиды. Причём такая точка – единственная. Значит найденная точка, лежащая на оси пирамиды, является центром шара, описанного около данной пирамиды.
Что и требовалось доказать.
Пример 2
Доказать, что в правильную пирамиду можно вписать шар и центр этого шара лежит на ее высоте.
Доказательство
 Рис. 4.
Рис. 4.
Рассмотрим правильную пирамиду (рис. 4).
Проведём высоту . Прямая является осью данной правильной пирамиды. Любая точка этой оси равноудалена от боковых граней этой пирамиды. Проведём апофему грани . Биссектриса угла пересекает высоту пирамиды в некоторой точке . По свойству биссектрисы точка равноудалена от сторон угла ( и ), а значит расстояния от точки до боковой грани и до основания одинаковы. Таким образом, точка , лежащая на высоте, равноудалена от всех граней данной пирамиды. Причём такая точка единственная, а значит является центром вписанного шара.
Что и требовалось доказать.
Пример 3
Найдите радиус шара, описанного около правильного тетраэдра с ребром .
Решение
 Рис. 5.
Рис. 5.
Дан правильный тетраэдр с ребром , вокруг которого описан шар (рис. 5).
Пусть – высота тетраэдра. Тогда точка является центром описанной вокруг треугольника окружности. Проведём высоту треугольника . Так как треугольник правильный, то является также медианой и биссектрисой этого треугольника.
.
Точка является центром треугольника и делит отрезок в отношении 2:1.
, .
Проведём из центра шара перпендикуляр к боковому ребру . Так как треугольник равнобедренный с основанием , то является медианой этого треугольника. Поэтому .
Треугольники и подобны, так как (прямые), (общий угол).
Из подобия треугольников и следует .
.
Ответ: .
Цилиндр и призма
Цилиндр вписан в призму, если основания цилиндра вписаны в основания призмы (рис. 6).
Цилиндр описан около призмы, если его основания описаны около оснований призмы (рис. 7).
 Рис. 6.
Рис. 6.
Из определения цилиндра, вписанного в призму, следует, что цилиндр можно вписать в призму только в том случае, если можно в основание призмы вписать окружность.
 Рис. 7.
Рис. 7.
То же самое касается и цилиндра, описанного около призмы. Около призмы можно описать цилиндр лишь в том случае, если можно описать окружность вокруг основания призмы.
Известно, что в любой треугольник можно вписать окружность и вокруг любого треугольника можно описать окружность. Это означает, что в любую треугольную призму можно вписать цилиндр и вокруг любой треугольной призмы можно описать цилиндр.
Пример 4
Цилиндр описан около правильной шестиугольной призмы. Найдите угол между диагональю её боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Решение
 Рис. 8.
Рис. 8.
Из условия задачи следует, что боковые грани призмы – квадраты, так как сторона шестиугольника, вписанного в окружность, равна радиусу (рис. 8). Рёбра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А угол между диагональю и стороной квадрата равен .
Ответ: .
Цилиндр и пирамида
Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной её основанию (рис. 9).
Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра (рис. 10).
 Рис. 9.
Рис. 9.
Очевидно, что высота вписанного в пирамиду цилиндра меньше высоты пирамиды. Если же цилиндр описан около пирамиды, то высота цилиндра равна высоте пирамиды.
 Рис. 10.
Рис. 10.
Из определений также следует, что если пирамида правильная, то в неё можно вписать цилиндр и около неё можно описать цилиндр.
Конус и призма
Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы (рис. 11).
Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса (рис. 12).
 Рис. 11.
Рис. 11.
Вписать конус можно только в такую призму, в основание которой можно вписать окружность.
 Рис. 12.
Рис. 12.
Если конус вписан в прямую призму, часть сечения комбинации тел плоскостью, проходящей через ось конуса, представляет собой прямоугольный треугольник, катеты которого — высота конуса (и призмы) и радиус конуса (и вписанной в основание призмы окружности), а гипотенуза — образующая конуса.
Высота конуса, описанного около призмы больше высоты призмы. Если же конус вписан в призму, то высота конуса равна высоте призмы.
Конус и пирамида
Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды (рис. 13).
Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды (рис. 14).
 Рис. 13.
Рис. 13.
Конус можно вписать в пирамиду только в том случае, если можно в основание пирамиды вписать окружность.
 Рис. 14.
Рис. 14.
Аналогично, около пирамиды можно описать конус лишь в том случае, если можно описать окружность вокруг основания пирамиды.
При этом как в случае вписанного в пирамиду конуса, так и в случае описанного около пирамиды конуса, высоты конуса и пирамиды совпадают.
Конус и цилиндр
Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра (рис. 15).
Конус описан около цилиндра, если одно из оснований цилиндра касается поверхности конуса, а другое его основание принадлежит основанию конуса (рис. 16).
 Рис. 15.
Рис. 15.
Очевидно, что в любой цилиндр можно вписать конус.
Оси цилиндра и вписанного в него конуса совпадают. Цилиндр и вписанный конус имеют равные высоты и радиусы.
 Рис. 16.
Рис. 16.
В любой конус можно вписать бесконечное множество цилиндров (радиусы цилиндров меньше радиуса конуса).
Центры оснований конуса и цилиндра совпадают, а высоты и радиусы различаются.
Упражнение
- Найдите радиус шара, описанного около куба с ребром .
- Докажите, что если в правильную призму можно вписать сферу, то центром сферы является середина отрезка, соединяющего центры оснований этой призмы.
- В правильную шестиугольную призму вписан шар радиуса 1. Найдите сторону основания и высоту призмы.
- Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 2.
Контрольные вопросы
- Какую сферу называют описанной около многогранника?
- Какую сферу называют вписанной в многогранник?
- Можно ли вокруг правильной пирамиды описать шар?
- Можно ли в правильную пирамиду вписать шар?
- Приведите примеры комбинации геометрических тел. Сделайте схематические рисунки.
Упражнение
1. .
3. , .
4. .


