- Равномерное движение по окружности
- Частота и период движения по окружности
- знать понятия: движение по окружности, вращательное движение, угловая скорость, 1 радиан, период и частота; векторный способ задания положения точечного тела в пространстве; закон равномерного движения точечного тела по окружности
- уметь задавать положение точечного тела в пространстве с помощью радиус-вектора; находить положение тела на окружности при заданном законе его движения; переводить градусы в радианы; находить период и частоту движения тела по окружности
- Дайте определение равномерного движения.
- Есть ли другие способы задания положения точечного тела в пространстве, помимо координатного?
- Каков период обращения Земли вокруг Солнца?
Равномерное движение по окружности
При движении по окружности траектория движения тела представляет собой окружность постоянного радиуса. Так движется конец стрелки часов, гоночная машина на круговой трассе. Приближённо можно считать, что и Земля вокруг Солнца, и Луна вокруг Земли двигаются по окружностям.
Движение по окружности — это такое движение точечного тела, при котором его траектория в выбранной системе отсчёта имеет форму окружности.
 Рис. 1. Пример движения по окружности
Рис. 1. Пример движения по окружности
Следует различать движение по окружности и вращательное движение: одна точка на стрелке механических часов движется по окружности, сама стрелка часов совершает вращательные движения вокруг неподвижного центра (рис. 1).
Вращательное движение тела — это такое движение тела, имеющего размеры, при котором все точки этого тела движутся по окружностям, расположенным в параллельных плоскостях.
Центры всех окружностей лежат на одной прямой, неподвижной в выбранной системе отсчёта, перпендикулярной к плоскостям окружностей и называемой осью вращения.
 Рис. 2. Вращение Земли
Рис. 2. Вращение Земли
Выше было сказано, что движение Земли вокруг Солнца в приближении можно считать движением по окружности. Одновременно с этим наша планета ещё вращается вокруг своей оси (рис. 2).
В данном параграфе мы не будем останавливаться на описании вращательного движения, но подробно изучим движение точечного тела по окружности.
Ранее для описания положения тела в пространстве в любой момент времени мы использовали только координатный метод. Данный метод применим для описания движения тела по окружности, однако математическое выражение закона изменения координат точечного тела при его движении по окружности очень трудоёмко, поэтому мы применим другой способ — векторный.
Векторный способ описания положения тела в пространстве предполагает использование радиус-вектора.
Радиус-вектор — это вектор, проведённый из начала координат системы отсчёта в точку пространства, где в данный момент находится рассматриваемое точечное тело.
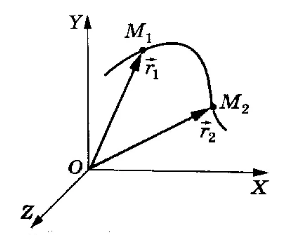 Рис. 3. Векторный способ задания положения тела в пространстве
Рис. 3. Векторный способ задания положения тела в пространстве
Рассмотрим рисунок 3: в начальный момент времени точечное тело находится в точке М1, его положение задаёт радиус-вектор .
При движении тела из точки М1 в точку М2 радиус-вектор изменяется как по направлению, так и по модулю: положение тела в точке М2 задаёт радиус вектор .
При движении точечного тела по окружности за начало координат принимается центр окружности, радиус-вектор будет изменять только своё направление, так как его длина в процессе движения всё время будет равна радиусу окружности.
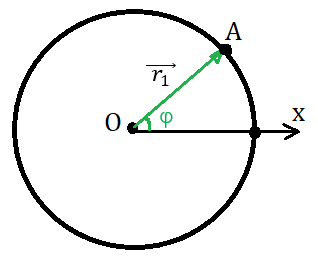 Рис. 4. Положение тела на окружности задаётся с помощью угла φ
Рис. 4. Положение тела на окружности задаётся с помощью угла φ
При движении точечного тела А по окружности будет изменяться угол — угол между радиус-вектором и осью ОХ (рис. 4).
Таким образом, чтобы описать движение тела по окружности, необходимо определить зависимость угла от времени t.
 Рис. 5. Угол АОВ соответствует 1 радиану
Рис. 5. Угол АОВ соответствует 1 радиану
Если известна зависимость , можно найти положение точечного тела в любой момент времени или, наоборот, найти момент времени, когда тело находится в заданной точке.
Угол может измеряться в градусах, но на практике часто применяется и другая единица измерения
угла — радианы (рад). Если длина дуги АВ равна радиусу окружности R, то угол = 1 рад (рис. 5).
Один радиан — это величина центрального угла окружности, опирающегося на дугу, длина которой равна радиусу окружности: .
Пусть закон движения точечного тела А, движущегося по окружности, имеет следующий вид:
.
Заметим, что при t = 0 угол между радиус-вектором и осью ОХ составляет , следовательно, величина задаёт начальное положение радиус-вектора.
Величина показывает, на какой угол поворачивается радиус-вектор за секунду.
Таким образом, это выражение аналогично закону изменения координаты точечного тела, движущегося равномерно прямолинейно .
Подставляя в выражение различные значения времени, найдём положения точечного тела А в соответствующие временные промежутки. Занесём полученные значения в таблицу 1.
Таблица 1. Положение тела на окружности в разные моменты времени
|
Время t
|
t = 0
|
t = 1
|
t = 2
|
t = 3
|
t = 4
|
|
Угол φ, рад
|
|
|
|
|
|
 Рис. 6. Положение точечного тела в разные моменты времени
Рис. 6. Положение точечного тела в разные моменты времени
Отметим на окружности полученные положения точечного тела А (рис. 6).
Начальный угол между между радиус-вектором и осью ОХ обозначается . В рассматриваемой задаче .
Величина показывает величину изменения угла в единицу времени.
Физическая величина, характеризующая быстроту изменения угла , называется угловой скоростью (греческая буква «омега») и рассчитывается по следующей формуле:
,
где рад — угол поворота радиус-вектора точечного тела за время ;
с — время.
Угловая скорость — это величина, равная отношению угла поворота радиус-вектора точечного тела, движущегося по окружности, за время к этому промежутку времени: .
Единица измерения угловой скорости в СИ, как видно из формулы, радиан в секунду (рад/с).
В приведённом примере угловая скорость равна:
.
При равномерном движении по окружности угловая скорость не меняется с течением времени .
Если угловая скорость точечного тела, движущегося по окружности, не меняется с течением времени, такое движение является равномерным.
В общем виде зависимость имеет следующий вид:
,
где [рад] — угол между радиус-вектором и осью ОХ в момент времени ;
[рад] — начальный угол;
[рад/с] — угловая скорость;
[с] — время.
Закон равномерного движения точечного тела по окружности:
.
Частота и период движения по окружности
Если точечное тело движется по окружности с постоянной угловой скоростью, то время, за которое тело делает один полный оборот, является фиксированной величиной, данная величина получила название период T.
Пусть точечное тело совершило 5 полных оборотов за t = 20 с. Понятно, что один оборот тело совершило за 4 секунды. Таким образом, период движения точечного тела по окружности можно найти по следующей формуле:
,
где [с] — период;
[с] — время, за которое тело совершило N оборотов;
— количество оборотов за время .
Период обращения — это время, за которое точечное тело, движущееся по окружности, совершает один оборот: .
Выразим из формулы угловой скорости величину Δt:
.
За один оборот точечное тело поворачивается на угол .
Тогда формулу периода можно записать в следующем виде:
.
Для описания движения тела по окружности также используется физическая величина, показывающая количество полных оборотов в единицу времени — данная величина называется частотой (греческая буква «ню»):
.
где [с-1] — частота;
Δt [с] — время, за которое тело совершило N оборотов;
N — количество оборотов за время Δt.
Частота обращения — это количество полных оборотов, совершённых точечным телом при движении по окружности за время Δt: .
Единица измерения частоты в СИ — секунда в минус первой степени (с-1) или герц (Гц).
Глядя на эти формулы, становится очевидно, что период обращения и частота — взаимно обратные величины:
.
Тогда для частоты будут справедливы следующие соотношения:
.
Понятия периода и частоты применимы не только к движение точечного тела по окружности, но и к вращательному движению тела, имеющего размеры. В этом случае период вращения — это время, за которое вращающееся тело делает один оборот; частота вращения — количество оборотов вращающегося тела за единицу времени.
Пример 1
Турбина, находящаяся в тепловой машине, совершает 480 оборотов за 30 секунд. Определите период, частоту и угловую скорость лопастей турбины.
Решение
1. Найдём период:
с.
2. Частоту мы можем найти двумя способами:
Гц или Гц.
3. Угловую скорость мы также можем найти двумя способами: через частоту или через период. Выразим, например, через период:
.
Ответ: .
Итоги
- Движение по окружности — это такое движение точечного тела, при котором его траектория в выбранной системе отсчёта имеет форму окружности.
- Радиус-вектор — это вектор, проведённый из начала координат системы отсчёта в точку пространства, где в данный момент находится рассматриваемое точечное тело.
- Угловая скорость — это величина, равная отношению угла поворота радиус-вектора точечного тела, движущегося по окружности, за время , к этому промежутку времени: .
- Закон равномерного движения точечного тела по окружности: .
- Период обращения — это время, за которое точечное тело, движущееся по окружности, совершает один оборот: .
- Частота обращения — это количество полных оборотов, совершённых точечным телом при движении по окружности за время: .
Упражнение 1
1. Колесо вращается, делая 600 оборотов в минуту. Определите период и частоту вращения колеса, а также его угловую скорость.
2. Закон равномерного движения тела по окружности выглядит следующим образом: . Чему равен начальный угол и угловая скорость?
Контрольные вопросы
1. Дайте определение угловой скорости. По каким формулам её можно рассчитать?
2. Что такое период обращения? По каким формулам его можно рассчитать?
3. Как перевести градусы в радианы?
Упражнение 1
1. .
2. .
- Равномерное движение по окружности
- Частота и период движения по окружности
- знать понятия: движение по окружности, вращательное движение, угловая скорость, 1 радиан, период и частота; векторный способ задания положения точечного тела в пространстве; закон равномерного движения точечного тела по окружности
- уметь задавать положение точечного тела в пространстве с помощью радиус-вектора; находить положение тела на окружности при заданном законе его движения; переводить градусы в радианы; находить период и частоту движения тела по окружности
- Дайте определение равномерного движения.
- Есть ли другие способы задания положения точечного тела в пространстве, помимо координатного?
- Каков период обращения Земли вокруг Солнца?
Равномерное движение по окружности
При движении по окружности траектория движения тела представляет собой окружность постоянного радиуса. Так движется конец стрелки часов, гоночная машина на круговой трассе. Приближённо можно считать, что и Земля вокруг Солнца, и Луна вокруг Земли двигаются по окружностям.
Движение по окружности — это такое движение точечного тела, при котором его траектория в выбранной системе отсчёта имеет форму окружности.
 Рис. 1. Пример движения по окружности
Рис. 1. Пример движения по окружности
Следует различать движение по окружности и вращательное движение: одна точка на стрелке механических часов движется по окружности, сама стрелка часов совершает вращательные движения вокруг неподвижного центра (рис. 1).
Вращательное движение тела — это такое движение тела, имеющего размеры, при котором все точки этого тела движутся по окружностям, расположенным в параллельных плоскостях.
Центры всех окружностей лежат на одной прямой, неподвижной в выбранной системе отсчёта, перпендикулярной к плоскостям окружностей и называемой осью вращения.
 Рис. 2. Вращение Земли
Рис. 2. Вращение Земли
Выше было сказано, что движение Земли вокруг Солнца в приближении можно считать движением по окружности. Одновременно с этим наша планета ещё вращается вокруг своей оси (рис. 2).
В данном параграфе мы не будем останавливаться на описании вращательного движения, но подробно изучим движение точечного тела по окружности.
Ранее для описания положения тела в пространстве в любой момент времени мы использовали только координатный метод. Данный метод применим для описания движения тела по окружности, однако математическое выражение закона изменения координат точечного тела при его движении по окружности очень трудоёмко, поэтому мы применим другой способ — векторный.
Векторный способ описания положения тела в пространстве предполагает использование радиус-вектора.
Радиус-вектор — это вектор, проведённый из начала координат системы отсчёта в точку пространства, где в данный момент находится рассматриваемое точечное тело.
 Рис. 3. Векторный способ задания положения тела в пространстве
Рис. 3. Векторный способ задания положения тела в пространстве
Рассмотрим рисунок 3: в начальный момент времени точечное тело находится в точке М1, его положение задаёт радиус-вектор .
При движении тела из точки М1 в точку М2 радиус-вектор изменяется как по направлению, так и по модулю: положение тела в точке М2 задаёт радиус вектор .
При движении точечного тела по окружности за начало координат принимается центр окружности, радиус-вектор будет изменять только своё направление, так как его длина в процессе движения всё время будет равна радиусу окружности.
 Рис. 4. Положение тела на окружности задаётся с помощью угла φ
Рис. 4. Положение тела на окружности задаётся с помощью угла φ
При движении точечного тела А по окружности будет изменяться угол — угол между радиус-вектором и осью ОХ (рис. 4).
Таким образом, чтобы описать движение тела по окружности, необходимо определить зависимость угла от времени t.
 Рис. 5. Угол АОВ соответствует 1 радиану
Рис. 5. Угол АОВ соответствует 1 радиану
Если известна зависимость , можно найти положение точечного тела в любой момент времени или, наоборот, найти момент времени, когда тело находится в заданной точке.
Угол может измеряться в градусах, но на практике часто применяется и другая единица измерения
угла — радианы (рад). Если длина дуги АВ равна радиусу окружности R, то угол = 1 рад (рис. 5).
Один радиан — это величина центрального угла окружности, опирающегося на дугу, длина которой равна радиусу окружности: .
Пусть закон движения точечного тела А, движущегося по окружности, имеет следующий вид:
.
Заметим, что при t = 0 угол между радиус-вектором и осью ОХ составляет , следовательно, величина задаёт начальное положение радиус-вектора.
Величина показывает, на какой угол поворачивается радиус-вектор за секунду.
Таким образом, это выражение аналогично закону изменения координаты точечного тела, движущегося равномерно прямолинейно .
Подставляя в выражение различные значения времени, найдём положения точечного тела А в соответствующие временные промежутки. Занесём полученные значения в таблицу 1.
Таблица 1. Положение тела на окружности в разные моменты времени
|
Время t
|
t = 0
|
t = 1
|
t = 2
|
t = 3
|
t = 4
|
|
Угол φ, рад
|
|
|
|
|
|
 Рис. 6. Положение точечного тела в разные моменты времени
Рис. 6. Положение точечного тела в разные моменты времени
Отметим на окружности полученные положения точечного тела А (рис. 6).
Начальный угол между между радиус-вектором и осью ОХ обозначается . В рассматриваемой задаче .
Величина показывает величину изменения угла в единицу времени.
Физическая величина, характеризующая быстроту изменения угла , называется угловой скоростью (греческая буква «омега») и рассчитывается по следующей формуле:
,
где рад — угол поворота радиус-вектора точечного тела за время ;
с — время.
Угловая скорость — это величина, равная отношению угла поворота радиус-вектора точечного тела, движущегося по окружности, за время к этому промежутку времени: .
Единица измерения угловой скорости в СИ, как видно из формулы, радиан в секунду (рад/с).
В приведённом примере угловая скорость равна:
.
При равномерном движении по окружности угловая скорость не меняется с течением времени .
Если угловая скорость точечного тела, движущегося по окружности, не меняется с течением времени, такое движение является равномерным.
В общем виде зависимость имеет следующий вид:
,
где [рад] — угол между радиус-вектором и осью ОХ в момент времени ;
[рад] — начальный угол;
[рад/с] — угловая скорость;
[с] — время.
Закон равномерного движения точечного тела по окружности:
.
Частота и период движения по окружности
Если точечное тело движется по окружности с постоянной угловой скоростью, то время, за которое тело делает один полный оборот, является фиксированной величиной, данная величина получила название период T.
Пусть точечное тело совершило 5 полных оборотов за t = 20 с. Понятно, что один оборот тело совершило за 4 секунды. Таким образом, период движения точечного тела по окружности можно найти по следующей формуле:
,
где [с] — период;
[с] — время, за которое тело совершило N оборотов;
— количество оборотов за время .
Период обращения — это время, за которое точечное тело, движущееся по окружности, совершает один оборот: .
Выразим из формулы угловой скорости величину Δt:
.
За один оборот точечное тело поворачивается на угол .
Тогда формулу периода можно записать в следующем виде:
.
Для описания движения тела по окружности также используется физическая величина, показывающая количество полных оборотов в единицу времени — данная величина называется частотой (греческая буква «ню»):
.
где [с-1] — частота;
Δt [с] — время, за которое тело совершило N оборотов;
N — количество оборотов за время Δt.
Частота обращения — это количество полных оборотов, совершённых точечным телом при движении по окружности за время Δt: .
Единица измерения частоты в СИ — секунда в минус первой степени (с-1) или герц (Гц).
Глядя на эти формулы, становится очевидно, что период обращения и частота — взаимно обратные величины:
.
Тогда для частоты будут справедливы следующие соотношения:
.
Понятия периода и частоты применимы не только к движение точечного тела по окружности, но и к вращательному движению тела, имеющего размеры. В этом случае период вращения — это время, за которое вращающееся тело делает один оборот; частота вращения — количество оборотов вращающегося тела за единицу времени.
Пример 1
Турбина, находящаяся в тепловой машине, совершает 480 оборотов за 30 секунд. Определите период, частоту и угловую скорость лопастей турбины.
Решение
1. Найдём период:
с.
2. Частоту мы можем найти двумя способами:
Гц или Гц.
3. Угловую скорость мы также можем найти двумя способами: через частоту или через период. Выразим, например, через период:
.
Ответ: .
Итоги
- Движение по окружности — это такое движение точечного тела, при котором его траектория в выбранной системе отсчёта имеет форму окружности.
- Радиус-вектор — это вектор, проведённый из начала координат системы отсчёта в точку пространства, где в данный момент находится рассматриваемое точечное тело.
- Угловая скорость — это величина, равная отношению угла поворота радиус-вектора точечного тела, движущегося по окружности, за время , к этому промежутку времени: .
- Закон равномерного движения точечного тела по окружности: .
- Период обращения — это время, за которое точечное тело, движущееся по окружности, совершает один оборот: .
- Частота обращения — это количество полных оборотов, совершённых точечным телом при движении по окружности за время: .
Упражнение 1
1. Колесо вращается, делая 600 оборотов в минуту. Определите период и частоту вращения колеса, а также его угловую скорость.
2. Закон равномерного движения тела по окружности выглядит следующим образом: . Чему равен начальный угол и угловая скорость?
Контрольные вопросы
1. Дайте определение угловой скорости. По каким формулам её можно рассчитать?
2. Что такое период обращения? По каким формулам его можно рассчитать?
3. Как перевести градусы в радианы?
Упражнение 1
1. .
2. .



