- Прямолинейное равномерное движение
- Прямолинейное равноускоренное движение
- Примеры решения задач
- знать понятия «равномерное движение», «равноускоренное движение»; уравнение движения при прямолинейном равномерном движении; уравнение скорости и уравнение движения при прямолинейном равноускоренном движении
- уметь находить координату прямолинейно движущегося тела в различные моменты времени; находить скорость тела, движущегося равноускоренно, в различные моменты времени
- Куда направлен вектор скорости тела (по направлению движения или против), если его координата изменилась от x0 = 0 до x = 20 м?
- Как называется движение, при котором через равные промежутки времени скорость тела изменяется на одну и ту же величину?
- Как найти координату прямолинейно движущегося тела?
Прямолинейное равномерное движение
Вам уже известно, что при равномерном движении скорость тела с течением времени не изменяется.
Равномерное движение — это движение с постоянной скоростью, при котором тело за равные промежутки времени проходит равные расстояния.
Если тело движется равномерно и при этом не изменяет направление своего движения, такое движение называется равномерным прямолинейным.
 Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Пусть автомобиль движется в положительном направлении оси ОХ с постоянной скоростью.
В момент времени t = 0 тело находится в координате x0 = 100 м (рис. 1). Через 20 секунд автомобиль оказался в точке с координатой x = 300 м. Так как за 20 секунд автомобилем пройдено 200 метров, скорость данного тела равна м/с.
Зная, что тело движется равномерно, можно утверждать, что значение начальной координаты x0 автомобиля каждую секунду увеличивается на 10 метров.
Тогда конечную координату в момент времени t будет определять следующая формула:
,
где — конечная координата тела;
— начальная координата тела;
— скорость равномерного движения;
— время, через которое точечное тело окажется в координате x.
Учтите: если вектор скорости сонаправлен с координатной осью, то в формуле выше скорость имеет знак «+»; если вектор скорости направлен в противоположную сторону — знак «−».
Данное уравнение представляет собой зависимость координаты равномерно прямолинейно движущегося тела от времени и называется законом (уравнением) движения.
Изменение координаты любого тела, имеющего постоянную скорость и направление движения, можно описать уравнением движения.
Подставим в формулу выше координаты и скорость автомобиля:
.
Понятно, что, подставляя в данную формулу различные значения времени t, можно найти координату тела в заданный момент времени.
Например, рассчитаем координату автомобиля через 1 минуту:
.
При необходимости это уравнение можно использовать, чтобы найти промежуток времени, через который тело из точки с координатой x0 переместится в точку с координатой x.
Найдём время, которое понадобится автомобилю, чтобы оказаться в координате 1 500 м. Для этого выразим из формулы время:
.
Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
Прямолинейное равноускоренное движение
Если скорость тела изменяется со временем, то есть за равные промежутки времени тело проходит разные расстояния, такое движение называется ускоренным. Ускорение характеризует быстроту изменения модуля и направления скорости.
Если каждую секунду скорость тела изменяется на одинаковую величину, то ускорение тела не изменяется с течением времени — такое движение называется равноускоренным.
Если в процессе движения ускорение тела остаётся величиной постоянной, такое движение называется равноускоренным.
Ускорение показывает, на сколько метров в секунду увеличивается (или уменьшается) начальная скорость тела каждую секунду движения. Следовательно, конечную скорость можно найти по следующей формуле:
,
где — конечная скорость тела;
—начальная скорость тела;
— ускорение тела;
— время, за которое значение скорости изменилось от v0 до v.
Данная формула называется уравнением скорости или законом изменения скорости.
Знаки величин , и определяются в зависимости от направления соответствующих векторов.
Если векторы скоростей и сонаправлены с координатной осью, то в формуле выше скорости имеют знак «+»; если векторы направлены в противоположную сторону — знак «−». Аналогичным способом определяется знак ускорения.
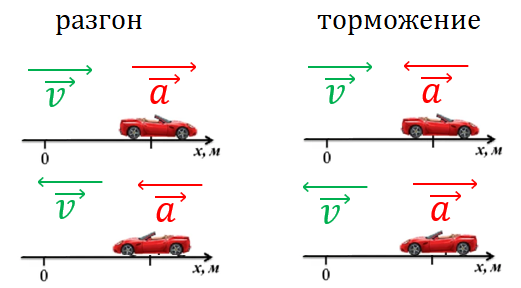 Рис. 2. Направление векторов скорости и ускорения при разгоне и торможении тела
Рис. 2. Направление векторов скорости и ускорения при разгоне и торможении тела
Напомним: если векторы скорости и ускорения имеют одинаковое направление, то скорость тела увеличивается — тело разгоняется; если векторы направлены в разные стороны — тело тормозит (рис. 2).
Закон движения (уравнение координаты) при прямолинейном равноускоренном движении имеет следующий вид:
.
Отметим, что, если для некоторого точечного тела заданы уравнения скорости и координаты, легко можно найти скорость и координату данного тела в любой момент времени.
Уравнение скорости при прямолинейном равноускоренном движении имеет следующий вид: .
Уравнение движения при прямолинейном равноускоренном движении имеет следующий вид: .
Примеры решения задач
Пример 1
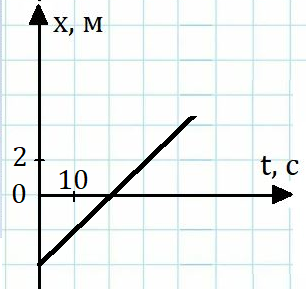 Рис. 3. Иллюстрация к примеру 1
Рис. 3. Иллюстрация к примеру 1
На рисунке 3 приведена зависимость координаты от времени для некоторого точечного тела, движущегося равномерно прямолинейно. Используя график, запишите уравнение движения для данного тела.
Решение
Чтобы записать уравнение координаты для равномерно движущегося тела, необходимо определить начальную координату x0 и скорость .
Из графика видно, что начальная координата равна x0 = −4 м.
Для определения скорости равномерно движущегося тела следует взять некоторый промежуток времени, например, от t = 0 до t = 20 с, и определить пройденное за это время расстояние:
.
Следовательно, за 20 с тело прошло путь 4 м.
Тогда скорость данного тела равна
.
Так как координата времени с течением времени увеличивается, тело движется в положительном направлении оси ОХ. Следовательно, в уравнении движения скорость будет иметь знак «+».
Остаётся подставить найденные значения в формулу:
.
Ответ: .
Пример 2
Известно, что уравнение движения для некоторого точечного тела имеет следующий вид:
.
А. Найдите координату данного тела через 10 с;
Б. Запишите уравнение скорости данного тела;
В. Найдите время, через которое скорость тела будет равна 42 м/с.
Решение
А. Рассчитаем искомую координату, для этого подставим в заданное уравнение движения время t = 10 c:
.
Б. Чтобы записать уравнение скорости для равноускоренно движущегося тела, необходимо определить начальную скорость и ускорение .
Вспомним общий вид уравнения координаты равномерно движущегося тела и сравним его с заданным уравнением:
,
.
Очевидно, что начальная координата тела x0 = 0, начальная скорость равна = 2 м/с, ускорение данного тела равно а = 10 м/с2.
Тогда закон изменения скорости имеет следующий вид:
.
В. Выразим из полученного уравнения скорости время и подставим предложенную скорость:
.
Ответ: а) ; б) ; в) .
Итоги
- Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
- Уравнение скорости при прямолинейном равноускоренном движении имеет следующий вид: .
- Уравнение движения при прямолинейном равноускоренном движении имеет следующий вид: .
Упражнение 1
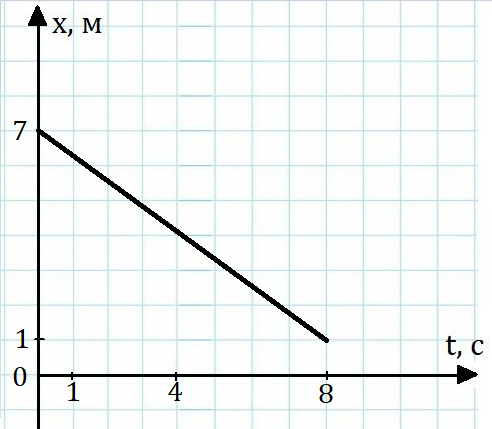 Рис. 4. Иллюстрация к задаче 1
Рис. 4. Иллюстрация к задаче 1
1. На рисунке 4 приведена зависимость координаты от времени для некоторого точечного тела, движущегося равномерно прямолинейно. Используя график, запишите уравнение движения для данного тела.
2. Известно, что уравнение скорости для некоторого точечного тела имеет следующий вид: . Постройте график скорости для данного тела.
3. Известно, что уравнение движения для некоторого точечного тела имеет следующий вид: .
А. Найдите координату данного тела через 2 с;
Б. Запишите уравнение скорости данного тела.
В. Найдите время, через которое скорость тела будет равна нулю.
Контрольные вопросы
1. Дайте определение равномерного прямолинейного движения.
2. В каком случае тело тормозит?
3. Сформулируйте общий вид уравнения движения для тела, движущегося прямолинейно равноускоренно.
Упражнение 1
1. x = 7 – 0,75t
2.
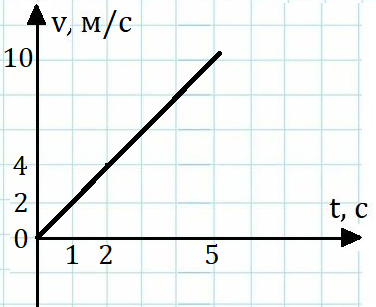
3. а) х = 21 м; б) = 12 – 4t; в) t = 3 c
- Прямолинейное равномерное движение
- Прямолинейное равноускоренное движение
- Примеры решения задач
- знать понятия «равномерное движение», «равноускоренное движение»; уравнение движения при прямолинейном равномерном движении; уравнение скорости и уравнение движения при прямолинейном равноускоренном движении
- уметь находить координату прямолинейно движущегося тела в различные моменты времени; находить скорость тела, движущегося равноускоренно, в различные моменты времени
- Куда направлен вектор скорости тела (по направлению движения или против), если его координата изменилась от x0 = 0 до x = 20 м?
- Как называется движение, при котором через равные промежутки времени скорость тела изменяется на одну и ту же величину?
- Как найти координату прямолинейно движущегося тела?
Прямолинейное равномерное движение
Вам уже известно, что при равномерном движении скорость тела с течением времени не изменяется.
Равномерное движение — это движение с постоянной скоростью, при котором тело за равные промежутки времени проходит равные расстояния.
Если тело движется равномерно и при этом не изменяет направление своего движения, такое движение называется равномерным прямолинейным.
 Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Пусть автомобиль движется в положительном направлении оси ОХ с постоянной скоростью.
В момент времени t = 0 тело находится в координате x0 = 100 м (рис. 1). Через 20 секунд автомобиль оказался в точке с координатой x = 300 м. Так как за 20 секунд автомобилем пройдено 200 метров, скорость данного тела равна м/с.
Зная, что тело движется равномерно, можно утверждать, что значение начальной координаты x0 автомобиля каждую секунду увеличивается на 10 метров.
Тогда конечную координату в момент времени t будет определять следующая формула:
,
где — конечная координата тела;
— начальная координата тела;
— скорость равномерного движения;
— время, через которое точечное тело окажется в координате x.
Учтите: если вектор скорости сонаправлен с координатной осью, то в формуле выше скорость имеет знак «+»; если вектор скорости направлен в противоположную сторону — знак «−».
Данное уравнение представляет собой зависимость координаты равномерно прямолинейно движущегося тела от времени и называется законом (уравнением) движения.
Изменение координаты любого тела, имеющего постоянную скорость и направление движения, можно описать уравнением движения.
Подставим в формулу выше координаты и скорость автомобиля:
.
Понятно, что, подставляя в данную формулу различные значения времени t, можно найти координату тела в заданный момент времени.
Например, рассчитаем координату автомобиля через 1 минуту:
.
При необходимости это уравнение можно использовать, чтобы найти промежуток времени, через который тело из точки с координатой x0 переместится в точку с координатой x.
Найдём время, которое понадобится автомобилю, чтобы оказаться в координате 1 500 м. Для этого выразим из формулы время:
.
Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
Прямолинейное равноускоренное движение
Если скорость тела изменяется со временем, то есть за равные промежутки времени тело проходит разные расстояния, такое движение называется ускоренным. Ускорение характеризует быстроту изменения модуля и направления скорости.
Если каждую секунду скорость тела изменяется на одинаковую величину, то ускорение тела не изменяется с течением времени — такое движение называется равноускоренным.
Если в процессе движения ускорение тела остаётся величиной постоянной, такое движение называется равноускоренным.
Ускорение показывает, на сколько метров в секунду увеличивается (или уменьшается) начальная скорость тела каждую секунду движения. Следовательно, конечную скорость можно найти по следующей формуле:
,
где — конечная скорость тела;
—начальная скорость тела;
— ускорение тела;
— время, за которое значение скорости изменилось от v0 до v.
Данная формула называется уравнением скорости или законом изменения скорости.
Знаки величин , и определяются в зависимости от направления соответствующих векторов.
Если векторы скоростей и сонаправлены с координатной осью, то в формуле выше скорости имеют знак «+»; если векторы направлены в противоположную сторону — знак «−». Аналогичным способом определяется знак ускорения.
 Рис. 2. Направление векторов скорости и ускорения при разгоне и торможении тела
Рис. 2. Направление векторов скорости и ускорения при разгоне и торможении тела
Напомним: если векторы скорости и ускорения имеют одинаковое направление, то скорость тела увеличивается — тело разгоняется; если векторы направлены в разные стороны — тело тормозит (рис. 2).
Закон движения (уравнение координаты) при прямолинейном равноускоренном движении имеет следующий вид:
.
Отметим, что, если для некоторого точечного тела заданы уравнения скорости и координаты, легко можно найти скорость и координату данного тела в любой момент времени.
Уравнение скорости при прямолинейном равноускоренном движении имеет следующий вид: .
Уравнение движения при прямолинейном равноускоренном движении имеет следующий вид: .
Примеры решения задач
Пример 1
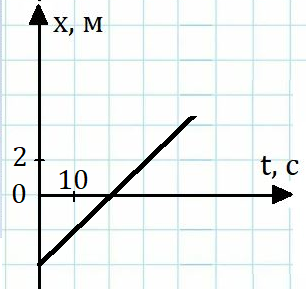 Рис. 3. Иллюстрация к примеру 1
Рис. 3. Иллюстрация к примеру 1
На рисунке 3 приведена зависимость координаты от времени для некоторого точечного тела, движущегося равномерно прямолинейно. Используя график, запишите уравнение движения для данного тела.
Решение
Чтобы записать уравнение координаты для равномерно движущегося тела, необходимо определить начальную координату x0 и скорость .
Из графика видно, что начальная координата равна x0 = −4 м.
Для определения скорости равномерно движущегося тела следует взять некоторый промежуток времени, например, от t = 0 до t = 20 с, и определить пройденное за это время расстояние:
.
Следовательно, за 20 с тело прошло путь 4 м.
Тогда скорость данного тела равна
.
Так как координата времени с течением времени увеличивается, тело движется в положительном направлении оси ОХ. Следовательно, в уравнении движения скорость будет иметь знак «+».
Остаётся подставить найденные значения в формулу:
.
Ответ: .
Пример 2
Известно, что уравнение движения для некоторого точечного тела имеет следующий вид:
.
А. Найдите координату данного тела через 10 с;
Б. Запишите уравнение скорости данного тела;
В. Найдите время, через которое скорость тела будет равна 42 м/с.
Решение
А. Рассчитаем искомую координату, для этого подставим в заданное уравнение движения время t = 10 c:
.
Б. Чтобы записать уравнение скорости для равноускоренно движущегося тела, необходимо определить начальную скорость и ускорение .
Вспомним общий вид уравнения координаты равномерно движущегося тела и сравним его с заданным уравнением:
,
.
Очевидно, что начальная координата тела x0 = 0, начальная скорость равна = 2 м/с, ускорение данного тела равно а = 10 м/с2.
Тогда закон изменения скорости имеет следующий вид:
.
В. Выразим из полученного уравнения скорости время и подставим предложенную скорость:
.
Ответ: а) ; б) ; в) .
Итоги
- Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
- Уравнение скорости при прямолинейном равноускоренном движении имеет следующий вид: .
- Уравнение движения при прямолинейном равноускоренном движении имеет следующий вид: .
Упражнение 1
 Рис. 4. Иллюстрация к задаче 1
Рис. 4. Иллюстрация к задаче 1
1. На рисунке 4 приведена зависимость координаты от времени для некоторого точечного тела, движущегося равномерно прямолинейно. Используя график, запишите уравнение движения для данного тела.
2. Известно, что уравнение скорости для некоторого точечного тела имеет следующий вид: . Постройте график скорости для данного тела.
3. Известно, что уравнение движения для некоторого точечного тела имеет следующий вид: .
А. Найдите координату данного тела через 2 с;
Б. Запишите уравнение скорости данного тела.
В. Найдите время, через которое скорость тела будет равна нулю.
Контрольные вопросы
1. Дайте определение равномерного прямолинейного движения.
2. В каком случае тело тормозит?
3. Сформулируйте общий вид уравнения движения для тела, движущегося прямолинейно равноускоренно.
Упражнение 1
1. x = 7 – 0,75t
2.
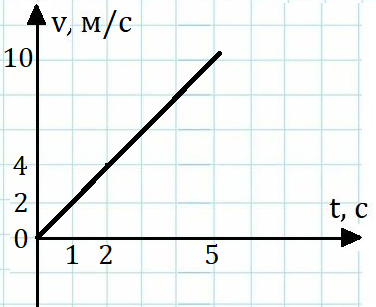
3. а) х = 21 м; б) = 12 – 4t; в) t = 3 c



