- Введение понятия показательного неравенства
- Формулировка утверждений, позволяющих решать показательные неравенства
- Решение показательных неравенств
- Знать определение показательного неравенства, методы его решения
- Уметь решать показательные неравенства различными методами
- Имеет ли смысл выражение ?
- Запишите числа в порядке убывания:
- Решить уравнение
Показательным неравенством называется неравенство вида
, (1)
где , и все сводящиеся к виду (1) неравенства.
При решении показательных неравенств используют свойства показательной функции:
- Если , то неравенство справедливо тогда и только тогда, когда .
- Если , то неравенство справедливо тогда и только тогда, когда .
Для того, чтобы свести неравенство к виду (1) применяют те же преобразования, что и при решении показательных уравнений: разложение левой части неравенства на множители, применение свойств степени, замена переменной.
Пример 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Решение
а)
Ответ: .
б)
Пусть , тогда неравенство примет вид . Решив последнее неравенство, получим . Вернемся к исходной переменной:
. Так как для любого x, то .
Ответ: .
в)
Так как правая часть неравенства положительна, поделим обе части неравенства на , получим
Решение последнего неравенство: .
Ответ: .
г) .
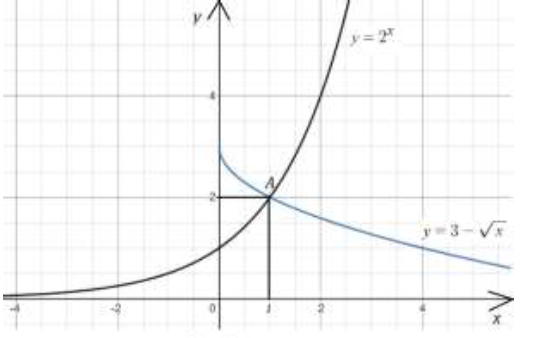 Рис. 1
Рис. 1
Решим это неравенство графически. В одной и той же системе координат построим графики функций и
Графики пересекаются в точке А(1;2). Решением исходного неравенства является промежуток .
Ответ: .
Упражнение 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Контрольные вопросы:
1. Какое утверждение верно, если :
1) неравенство равносильно неравенству ;
2) неравенство равносильно неравенству ?
2. Какое утверждение верно, если :
1) неравенство равносильно неравенству ;
2) неравенство равносильно неравенству ?
Упражнение 1
а) ; б) ; в) ; г) .
- Введение понятия показательного неравенства
- Формулировка утверждений, позволяющих решать показательные неравенства
- Решение показательных неравенств
- Знать определение показательного неравенства, методы его решения
- Уметь решать показательные неравенства различными методами
- Имеет ли смысл выражение ?
- Запишите числа в порядке убывания:
- Решить уравнение
Показательным неравенством называется неравенство вида
, (1)
где , и все сводящиеся к виду (1) неравенства.
При решении показательных неравенств используют свойства показательной функции:
- Если , то неравенство справедливо тогда и только тогда, когда .
- Если , то неравенство справедливо тогда и только тогда, когда .
Для того, чтобы свести неравенство к виду (1) применяют те же преобразования, что и при решении показательных уравнений: разложение левой части неравенства на множители, применение свойств степени, замена переменной.
Пример 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Решение
а)
Ответ: .
б)
Пусть , тогда неравенство примет вид . Решив последнее неравенство, получим . Вернемся к исходной переменной:
. Так как для любого x, то .
Ответ: .
в)
Так как правая часть неравенства положительна, поделим обе части неравенства на , получим
Решение последнего неравенство: .
Ответ: .
г) .
 Рис. 1
Рис. 1
Решим это неравенство графически. В одной и той же системе координат построим графики функций и
Графики пересекаются в точке А(1;2). Решением исходного неравенства является промежуток .
Ответ: .
Упражнение 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Контрольные вопросы:
1. Какое утверждение верно, если :
1) неравенство равносильно неравенству ;
2) неравенство равносильно неравенству ?
2. Какое утверждение верно, если :
1) неравенство равносильно неравенству ;
2) неравенство равносильно неравенству ?
Упражнение 1
а) ; б) ; в) ; г) .



