Конспект урока: Показательные уравнения

Методы решения показательных уравнений

1. Метод уравнивания показателей. Он основан на теореме о том, что уравнение

                                                                              $a^{f\left(x\right)}=a^{g\left(x\right)}$                                 (1)                      

равносильно уравнению $f\left(x\right)=g\left(x\right), где a>0,a\ne 1$.

Решить уравнение $0,3^{6-3x}=0,09.$

Решение

$0,3^{6-3x}=0,09,$

$0,3^{6-3x}=0,3^2$,

$6-3x=2$

$x=\frac{4}{3}$

$x=1\frac{1}{3}$

Ответ: $1\frac{1}{3}$.

2. Иногда, чтобы привести показательное уравнение к виду (1), нужно разложить левую часть уравнения на множители, в частности, вынести за скобки общий множитель, например:

$a^{x+1}-a^{x-1}=b$

$a^x(a-\frac{1}{a})=b$, и т.д.

Или, например, разделить обе части уравнения на выражение, не равное нулю, например:

$a^x=b^x$

$\frac{a^x}{b^x}=1$

${\left(\frac{a}{b}\right)}^x=1$ и т.д.

Решить уравнение $3^{x-2}-3^{x-3}=6$.

Решение

$3^{x-2}-3^{x-3}=6$,

$3^{x-2}(1-\frac{1}{3})=6$,

$3^{x-2}=9$,

$x-2=2,$

$x=4.$

Ответ: 4.

3. Метод введения новой переменной. Главное, помнить, что показательная функция не может принимать отрицательные значения.

Решить уравнение ${25}^x+4\times 5^x-5=0$

Решение

${25}^x+4\times 5^x-5=0$

Пусть $5^x=t,t>0$. Тогда уравнение примет вид:

$t^2+4t-5=0$,

$t_1=1;t_2=-5$.

Корень $t_2=-5$ не подходит, т.к. он отрицательный. Вернемся к исходной переменной:

$5^x=1,$

$x=0.$

Ответ: 0.

4. Функционально-графический метод решения показательного уравнения. В одной и той же системе координат строят графики левой и правой частей уравнения, находят значения абсцисс точек пересечения графиков. По возможности, производят проверку с целью уточнения корня уравнения.

Решить уравнение $9^{|x+2|}=3$.

Решение

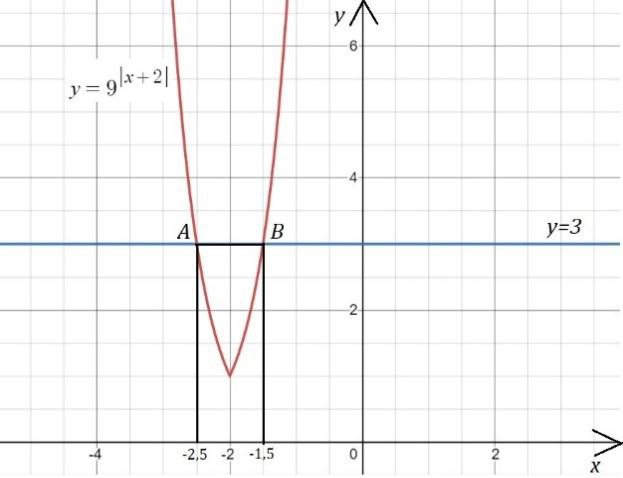Рис. 1

В одной и той же системе координат построим графики функции $y=9^{\left|x+2\right|}$ и $y=3$ (рис. 1).

 

Графики функций пересекаются в двух точках А(-2,5; 3) и В(-1,5; 3). Абсциссы этих точек и будут решениями исходного уравнения, т.е. $x_1=-2,5,x_2=-1,5$.

 

Проверка: если $x=-2,5$, то $9^{\left|-2,5+2\right|}=3$,  

$9^{0,5}=3$ – верно, значит $x=-2,5$ является корнем уравнения;  

если $x=-1,5$, то $9^{\left|-1,5+2\right|}=3$,  $9^{0,5}=3$  – верно, тогда $x=-1,5$ тоже является корнем исходного уравнения.

 

Ответ: -2,5; -1,5.

Замечание: при решении уравнения $f\left(x\right)=g\left(x\right)$, где $y=f\left(x\right)$ – убывающая функция, а  $y=g\left(x\right)$  – возрастающая функция (и наоборот) на одном и том же промежутке, и на этом промежутке находится корень уравнения, то этот корень будет единственным на данном промежутке.

Решить уравнение:
 

а) ${\left(\frac{1}{3}\right)}^{5-2x}=27$;     б) $4^{x-3}+4^x=65$;      в) $9^x-10\times 3^x+9=0$;      г) ${\sqrt{2}}^{\left|3-x\right|}=4$.

Итак:

1. Показательное уравнение – уравнение, в котором неизвестное содержится в показателе степени.
2. При решении показательного уравнения нужно свести исходное уравнению к виду $a^{f\left(x\right)}=a^{g\left(x\right)}$,  $a\ne 1,a>0$. Это можно сделать любым удобным способом: разложением левой части уравнения на множители, заменой переменной,  делению обеих частей уравнения на отличное от нуля выражение. Также иногда применим и функционально-графический метод решения.

1. Назовите основные методы решения показательных уравнений.
2. Верно ли, что уравнение $4^{3x-9}={64}^{x^2}$ равносильно уравнению $x-3=x^2$. Ответ обоснуйте.
3. Сколько корней имеет уравнение $5^x=5-x$? Ответ обоснуйте.