- Введение понятия логарифмического неравенства
- Алгоритм решения логарифмических неравенств
- Решение логарифмических неравенств
- Знать, что такое логарифмическое неравенство, методы его решения
- Уметь решать логарифмические неравенства
1.Возрастающей или убывающей является функция
а) ; б) ; в) .
2. Записать числа:
а) в виде логарифма по основанию 2;
б) в виде логарифма по основанию 3.
3. Найти область определения функций:
а) ; б) ; в) .
Логарифмическими неравенствами называют неравенства вида
, (1)
где , и неравенства, сводящиеся к этому виду.
Вообще говоря, знак неравенства может быть любой . Далее в параграфе будем это учитывать.
Простейшие логарифмические неравенства вида
(2)
или
(3)
где , имеют решения при любом действительном b.
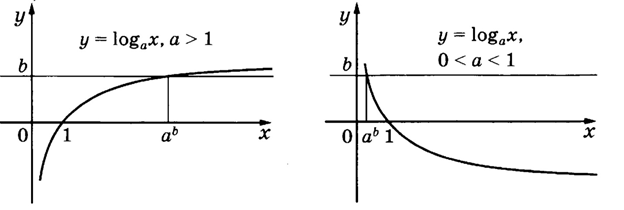
Рис. 1 Рис. 2
Если (см. рис. 1), то решение неравенства (2) — , неравенства (3) — .
Если (см. рис. 2), то решение неравенства (2) — , неравенства (3) — .
Алгоритм решения логарифмического неравенства
- Найти область допустимых значений неравенства.
- Представить (если это возможно) обе части неравенства в виде логарифма по одному и тому же основанию: .
- Определить, возрастающей или убывающей является логарифмическая функция : если , то функция возрастает, если , то убывает.
- Перейти к более простому неравенству, учитывая тот факт, что если функция возрастающая, то знак неравенства остается тем же, если убывающая, то меняется на противоположный.
- Решить полученное неравенство, записать ответ с учетом области допустимых значений, найденной в пункте 1.
Метод решения простейших неравенств вида (2), (3), описанный выше, вполне можно заменить этим алгоритмом.
Пример 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Решение
а) .
ОДЗ: .
Представим –1 в виде логарифма по основанию 0,5: . Исходное неравенство примет вид . Основание логарифмической функции находится в промежутке , значит, функция убывающая, при переходе от этого неравенства к более легкому, знак поменяется на противоположный, т.е.
С учетом области допустимых значений решение — .
Ответ:
б) .
Найдем область допустимых значений неравенства – логарифм определен на множестве положительных чисел, арифметический квадратный корень на множестве неотрицательных чисел, значит
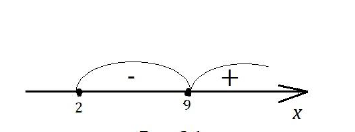 Рис. 3
Рис. 3
Решением второго неравенства системы является промежуток . Учитывая первое неравенство системы, получим ОДЗ .
Исходное неравенство решим методом интервалов, для этого найдем нули каждого множителя, нанесем их на числовую прямую с учетом области допустимых значений и определим знаки на каждом из получившихся промежутков.
или
Корень -2 не входит в ОДЗ.
Решением будет отрезок
Ответ:
в)
ОДЗ: .
Пусть , тогда неравенство примет вид , решив которое, найдем . Вернемся к исходной переменной:
Так как основание логарифма , то
Или .
Ответ: .
г) .
Запишем решение этого неравенства несколько иначе. Данное неравенство равносильно системе из трех неравенств:
которая в свою очередь равносильна каждой из систем
Значит, .
Ответ: .
Упражнение 1
Решить неравенство:
а) ;
б) ;
в) .
Контрольные вопросы
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
Упражнение 1
а) ; б) нет решений; в) .
- Введение понятия логарифмического неравенства
- Алгоритм решения логарифмических неравенств
- Решение логарифмических неравенств
- Знать, что такое логарифмическое неравенство, методы его решения
- Уметь решать логарифмические неравенства
1.Возрастающей или убывающей является функция
а) ; б) ; в) .
2. Записать числа:
а) в виде логарифма по основанию 2;
б) в виде логарифма по основанию 3.
3. Найти область определения функций:
а) ; б) ; в) .
Логарифмическими неравенствами называют неравенства вида
, (1)
где , и неравенства, сводящиеся к этому виду.
Вообще говоря, знак неравенства может быть любой . Далее в параграфе будем это учитывать.
Простейшие логарифмические неравенства вида
(2)
или
(3)
где , имеют решения при любом действительном b.
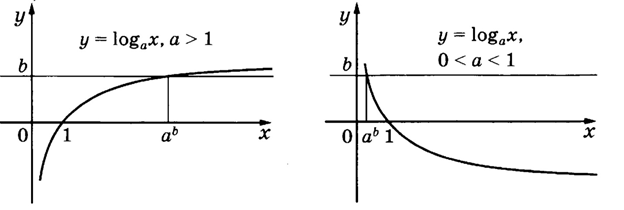
Рис. 1 Рис. 2
Если (см. рис. 1), то решение неравенства (2) — , неравенства (3) — .
Если (см. рис. 2), то решение неравенства (2) — , неравенства (3) — .
Алгоритм решения логарифмического неравенства
- Найти область допустимых значений неравенства.
- Представить (если это возможно) обе части неравенства в виде логарифма по одному и тому же основанию: .
- Определить, возрастающей или убывающей является логарифмическая функция : если , то функция возрастает, если , то убывает.
- Перейти к более простому неравенству, учитывая тот факт, что если функция возрастающая, то знак неравенства остается тем же, если убывающая, то меняется на противоположный.
- Решить полученное неравенство, записать ответ с учетом области допустимых значений, найденной в пункте 1.
Метод решения простейших неравенств вида (2), (3), описанный выше, вполне можно заменить этим алгоритмом.
Пример 1
Решить неравенство:
а) ;
б) ;
в) ;
г) .
Решение
а) .
ОДЗ: .
Представим –1 в виде логарифма по основанию 0,5: . Исходное неравенство примет вид . Основание логарифмической функции находится в промежутке , значит, функция убывающая, при переходе от этого неравенства к более легкому, знак поменяется на противоположный, т.е.
С учетом области допустимых значений решение — .
Ответ:
б) .
Найдем область допустимых значений неравенства – логарифм определен на множестве положительных чисел, арифметический квадратный корень на множестве неотрицательных чисел, значит
 Рис. 3
Рис. 3
Решением второго неравенства системы является промежуток . Учитывая первое неравенство системы, получим ОДЗ .
Исходное неравенство решим методом интервалов, для этого найдем нули каждого множителя, нанесем их на числовую прямую с учетом области допустимых значений и определим знаки на каждом из получившихся промежутков.
или
Корень -2 не входит в ОДЗ.
Решением будет отрезок
Ответ:
в)
ОДЗ: .
Пусть , тогда неравенство примет вид , решив которое, найдем . Вернемся к исходной переменной:
Так как основание логарифма , то
Или .
Ответ: .
г) .
Запишем решение этого неравенства несколько иначе. Данное неравенство равносильно системе из трех неравенств:
которая в свою очередь равносильна каждой из систем
Значит, .
Ответ: .
Упражнение 1
Решить неравенство:
а) ;
б) ;
в) .
Контрольные вопросы
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
- Если , верно ли, что равносильно ?
Упражнение 1
а) ; б) нет решений; в) .



