- Вычисление площади криволинейной трапеции
- Вычисление площади фигуры, ограниченной графиками двух непрерывных функций
- Уметь изображать на схематическом рисунке фигуру, ограниченную заданными линиями
- Знать формулу для вычисления площади фигуры, ограниченной графиками двух непрерывных функций
- Уметь вычислять площадь криволинейной трапеции
- Что такое криволинейная трапеция?
- Как связана площадь криволинейной трапеции с определённым интегралом
- Запишите формулу Ньютона-Лейбница
- Вычислите
Вычисление площади криволинейной трапеции
Как показывалось ранее, площадь криволинейной трапеции можно вычислить по формуле . Рассмотрим пример вычисления площади криволинейной трапеции.
Пример 1
Вычислить площадь фигуры, ограниченной прямыми , , осью и графиком функции .
Решение
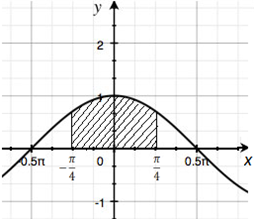 Рис. 1.
Рис. 1.
Фигура, площадь которой надо найти, изображена на рисунке 1. Она представляет собой криволинейную трапецию. Поэтому воспользуемся формулой
.
Ответ: .
Вычисление площади фигуры, ограниченной графиками двух непрерывных функций
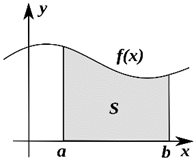 Рис. 2.
Рис. 2.
С помощью интеграла можно вычислять площади не только криволинейных трапеций вида, представленного на рисунке 2, но и плоских фигур более сложного вида.
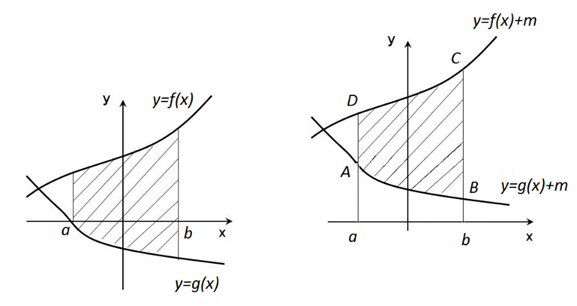 Рис. 3.
Рис. 3.
Рассмотрим фигуру, ограниченную прямыми , и графиками непрерывных функций , такими, что на отрезке выполняется условие (рис. 3а).
Выполним параллельный перенос данной фигуры на m единиц вверх
() так, чтобы данная фигура оказалась расположенной в координатной плоскости выше оси абсцисс (рис. 3б).
Теперь эта фигура ограничена сверху и снизу графиками функций и соответственно. При этом обе функции непрерывны и неотрицательны на отрезке . Найдём площадь этой фигуры:
.
Таким образом, получили следующее правило: площадь фигуры, ограниченной прямыми , и графиками функций , , непрерывных на отрезке и таких, что для всех x из отрезка выполняется неравенство , вычисляется по формуле
.
Пример 2
Вычислите площадь фигуры, ограниченной линиями , , , .
Решение
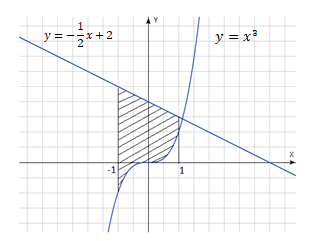 Рис. 4.
Рис. 4.
Построим данную фигуру (рис. 4).
Воспользуемся формулой
.
Ответ: 4.
Пример 3
Вычислите площадь фигуры, ограниченной линиями , .
Решение
 Рис. 5.
Рис. 5.
Построим данную фигуру (рис. 5) и найдём точки пересечения графиков функции, решив уравнение
.
Воспользуемся формулой
.
Ответ: .
Упражнение
1. Вычислите площадь фигуры, ограниченной прямыми , осью и графиком функции .
2. Вычислите площадь фигуры, ограниченной линиями , , , .
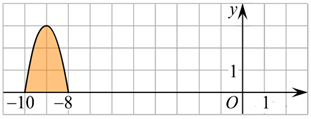 Рис. 6.
Рис. 6.
3. Вычислите площадь фигуры, ограниченной линиями , .
4. На рисунке 6 изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.
Контрольные вопросы
- Запишите формулу площади криволинейной трапеции.
- Запишите формулу площади фигуры, ограниченной графиками двух непрерывных функций.
Упражнение
- ;
- ;
- 9;
- 4.
