- Работа силы
- Мощность силы
- знать физический смысл и формулы работы и мощности силы
- уметь приводить примеры, когда работа силы отрицательна, положительна или равна нулю; вычислять работу и мощность силы
- Что такое работа силы?
- В каком случае работа силы отрицательна, а в каком положительна?
- Что характеризует мощность силы?
Работа силы
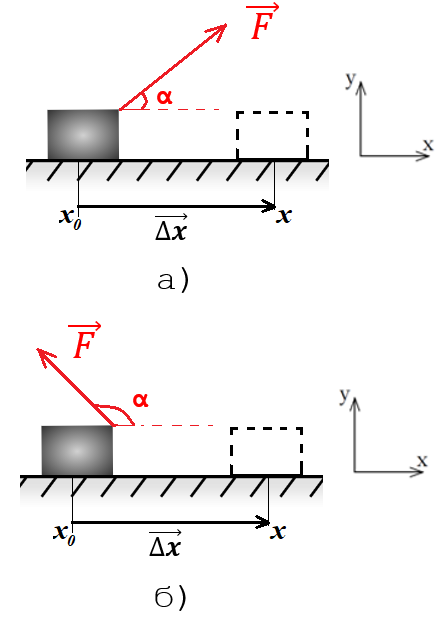 Рис. 1. Вычисление работы силы F, направленной под углом α к горизонту
Рис. 1. Вычисление работы силы F, направленной под углом α к горизонту
Если под действием известных сил материальная точка совершает определённое перемещение, то изменение скорости данной точки можно найти с помощью работы силы. Пусть под действием некоторой силы материальная точка совершает перемещение . Угол между векторами и равен (рис. 1).
В этом случае работа, совершённая над телом, прямо пропорциональна косинусу угла между вектором силы и вектором перемещения :
,
где [Дж] — работа, совершённая над телом;
[Н] — модуль силы, приложенной к телу;
[м] — модуль перемещения;
— угол между векторами и .
Работа постоянной силы — это скалярная физическая величина, равная произведению модуля силы и перемещения тела , умноженному на косинус угла между векторами и : .
Единица измерения механической работы в СИ — джоуль (Дж). Один джоуль — это работа постоянной по модулю силы, равной 1 Н, при перемещении тела на 1 м в направлении действия силы.
Чтобы выяснить физический смысл работы, рассмотрим рисунок 1. Пусть тело является материальной точкой, двигающейся только вдоль оси X. В случае, когда угол между векторами и лежит в пределах (рис. 1, а), косинус угла будет положителен , работа силы также положительна:
.
Если сумма остальных сил, действующих на данную материальную точку, равна нулю, то под действием силы тело будет разгоняться.
В противном случае, когда угол тупой (рис. 1, б), косинус данного угла отрицателен , работа силы также будет иметь отрицательное значение:
.
Когда сила совершает отрицательную работу, а сумма других сил, действующих на данное тело, равна нулю, тело приобретает отрицательное ускорение — оно будет тормозить.
Очевидно, что если вектор силы перпендикулярен вектору перемещения , то косинус угла между ними будет равен нулю , в этом случае сила не совершает работу .
Например, на тело, изображённое на рисунке 1, помимо силы действует сила тяжести , направленная под углом 90° к вектору перемещения . Работа силы тяжести при перемещении будет равна нулю.
Заметим, что произведение — это проекция силы на направление перемещения . Можно сказать, что работа силы равна произведению модуля перемещения на проекцию данной силы на направление перемещения.
Пусть на материальную точку действуют две силы и . Под действием этих сил точка совершает перемещение . Вектор перемещения сонаправлен с положительным направлением оси ОХ. Тогда работа силы равна , работа силы вычисляется аналогично .
Известно, что проекция равнодействующей на координатную ось равна сумме проекций всех сил, действующих на тело, на данную ось. Пусть .
Тогда проекция данной силы на ось ОХ равна:
.
Умножим левую и правую часть уравнения на модуль перемещения :
.
Получается, что работа суммы сил и равна сумме работ сил, действующих на тело:
.
Сумма работ всех действующих на материальную точку сил равна работе равнодействующей силы: .
Полученные закономерности справедливы при расчёте работы постоянной силы и постоянного угла между векторами и .
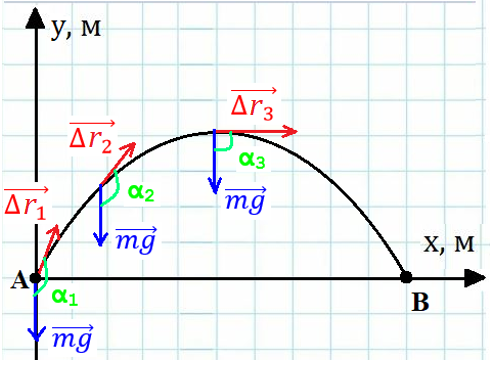 Рис. 2. Вычисление работы в случае, когда тело было брошено под углом к горизонту
Рис. 2. Вычисление работы в случае, когда тело было брошено под углом к горизонту
Рассмотрим случай, когда направление вектора перемещения , соответственно, и значение угла между векторами и меняется с течением времени.
Например, тело брошено под углом к горизонту (рис. 2). Требуется найти работу силы тяжести по перемещению тела из точки А в точку В.
В данном случае, чтобы вычислить работу, необходимо разбить перемещение материальной точки на достаточно малые перемещения ,, … такие, чтобы на протяжении каждого из данных перемещений модуль силы, совершающей работу, и угол между вектором перемещения и вектором силы можно было считать постоянными.
При выполнении этих условий работу на каждом из участков можно считать по формуле:
.
Полученные значения работ складываются:
.
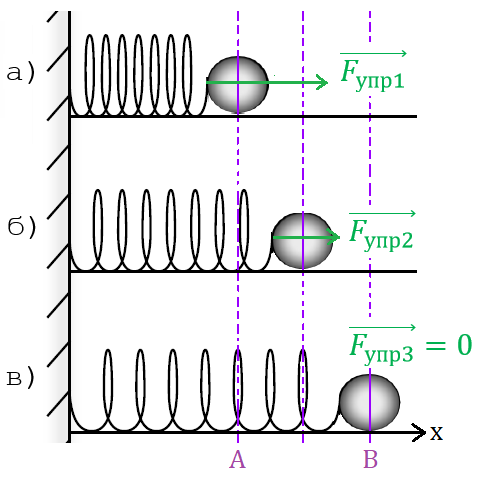 Рис. 3. Сила упругости совершает положительную работу
Рис. 3. Сила упругости совершает положительную работу
Рассмотрим ещё один пример.
Пусть пружину жёсткостью сжали на величину (рис. 3). Если перестать удерживать пружину, то под действием силы упругости она вернётся в недеформированное состояние — точку В. Сила упругости при этом совершит работу . Найдём величину этой работы.
Сила упругости, возникающая в пружине, прямо пропорциональна величине , следовательно, по мере движения шарика от точки А к точке В модуль силы упругости будет уменьшаться пропорционально её деформации от максимального значения вплоть до нуля .
На рисунке 4 показана зависимость модуля силы упругости от величины деформации пружины.
Нам уже известно, что, если сила, действующая на тело, изменяется с течением времени, для вычисления работы такой силы перемещение необходимо разбить на достаточно малые промежутки времени, на каждом из которых силу можно считать величиной постоянной.
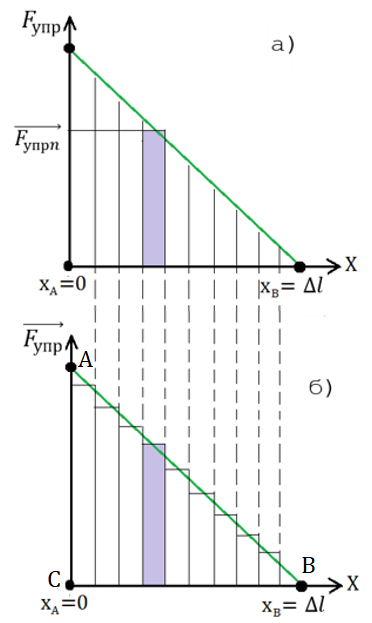 Рис. 4. Зависимость модуля силы упругости от величины деформации пружины
Рис. 4. Зависимость модуля силы упругости от величины деформации пружины
Пусть отрезок АВ представляет собой совокупность достаточно малых отрезков , , … и т. д. (рис. 4, а). Тогда модуль силы упругости на отрезке от до можно считать неизменным во времени.
Работа силы упругости на рассматриваемом участке равна . Из рисунка видно, что работа равна площади заштрихованного прямоугольника .
Очевидно, что на каждом достаточно малом участке работа силы упругости будет равна площади соответствующего прямоугольника (рис. 4, б).
Общая работа равна сумме работ на достаточно малых промежутках, следовательно, общая работа равна сумме площадей полученных прямоугольников . Чем больше вводится элементарных отрезков, тем точнее будет вычислена работа силы упругости.
При разбиении на достаточно малые промежутки отрезка АВ сумма площадей всех прямоугольников будет приблизительно равна площади прямоугольного треугольника АВС:
.
Если действующая на материальную точку сила не изменяет своего направления, а сама точка движется в направлении действия силы, то работа этой силы численно равна площади под графиком зависимости модуля силы от модуля перемещения рассматриваемой точки.
Мощность силы
Мощность силы характеризует скорость совершения работы. Например, необходимо поднять холодильник на третий этаж дома. Эту работу можно совершить вручную, используя силу мышц человека, поднявшись по ступеням лестницы. А можно загрузить холодильник в лифт, тогда работу по перемещению холодильника совершит подъёмный механизм лифта, а время совершения работы сократится на несколько минут. Понятно, что разница во времени совершении работы объясняется тем, что подъёмный механизм имеет большую мощность, нежели человек.
Мощность силы — это скалярная физическая величина, характеризующая быстроту совершения работы и равная отношению работы силы , совершённой за достаточно малый промежуток времени , длительности данного промежутка времени: , где .
Единица измерения мощности в СИ — ватт (Вт).
В случае, когда скорость совершения работы в каждый отдельно взятый момент времени не важна, применяется понятие средней мощности.
Средняя мощность — это скалярная физическая величина, равная отношению работы силы к промежутку времени , за который была совершена данная работа: .
Пусть под действием постоянной силы материальная точка движется со скоростью . За достаточно малый промежуток времени точка совершит перемещение . Тогда работа данной силы равна
,
где — угол между направлением вектора и вектора .
Мощность силы в данном случае можно вычислить по следующей формуле:
.
Пример 1
Строитель с помощью верёвки тянет дерево массой 80 кг по земле. Известно, что сила, с которой тянет строитель, направлена под углом к горизонту, а её модуль . За рассматриваемый промежуток времени тело переместилось на м. Определите:
а) работу силы тяжести дерева; б) работу силы трения, действующую на дерево, если коэффициент трения ; в) работу силы тяги.
Решение
1. Воспользуемся рисунком 1 под буквой а) и запишем формулу для работы по определению:
.
Будем использовать эту формулу, подставляя в неё различные силы, указанные в задаче.
2. Начнём с силы тяжести дерева. Поскольку сила тяжести направлена вертикально, а движение происходит в горизонтальном направлении, то работа равна нулю, так как :
.
3. Для определения работы силы трения вспомним формулу для силы трения-скольжения, где в нашей задаче . Сила трения будет направлена противоположно движению, а значит .
.
4. Работы силы тяги:
.
Ответ: ; ; .
Итоги
- Работа постоянной силы — это скалярная физическая величина, равная произведению модуля силы и перемещения тела , умноженному на косинус угла между векторами и : .
- Сумма работ всех действующих на материальную точку сил равна работе равнодействующей силы: .
- Если действующая на материальную точку сила не изменяет своего направления, а сама точка движется в направлении действия силы, то работа этой данной силы численно равна площади под графиком зависимости модуля силы от модуля перемещения рассматриваемой точки.
- Средняя мощность — это скалярная физическая величина, равная отношению работы силы к промежутку времени , за который была совершена данная работа: .
Упражнение 1
1. Груз массой 50 кг тянется по земле под действием силы тяги . Угол между направлением силы тяги и перемещением м равен . Определите работу равнодействующей силы, действующей на груз. Коэффициент трения груза о землю равен .
2. Средняя мощность лифта равна кВт. Какую работу совершит лифт за минуты?
Контрольные вопросы
1. В каком случае работа силы будет отрицательна?
2. Как рассчитать работу силы, если модуль силы изменяется с течением времени?
3. В чём заключается физический смысл мощности?
Упражнение 1
1. 371 Дж
2. 2,1 МДж
- Работа силы
- Мощность силы
- знать физический смысл и формулы работы и мощности силы
- уметь приводить примеры, когда работа силы отрицательна, положительна или равна нулю; вычислять работу и мощность силы
- Что такое работа силы?
- В каком случае работа силы отрицательна, а в каком положительна?
- Что характеризует мощность силы?
Работа силы
 Рис. 1. Вычисление работы силы F, направленной под углом α к горизонту
Рис. 1. Вычисление работы силы F, направленной под углом α к горизонту
Если под действием известных сил материальная точка совершает определённое перемещение, то изменение скорости данной точки можно найти с помощью работы силы. Пусть под действием некоторой силы материальная точка совершает перемещение . Угол между векторами и равен (рис. 1).
В этом случае работа, совершённая над телом, прямо пропорциональна косинусу угла между вектором силы и вектором перемещения :
,
где [Дж] — работа, совершённая над телом;
[Н] — модуль силы, приложенной к телу;
[м] — модуль перемещения;
— угол между векторами и .
Работа постоянной силы — это скалярная физическая величина, равная произведению модуля силы и перемещения тела , умноженному на косинус угла между векторами и : .
Единица измерения механической работы в СИ — джоуль (Дж). Один джоуль — это работа постоянной по модулю силы, равной 1 Н, при перемещении тела на 1 м в направлении действия силы.
Чтобы выяснить физический смысл работы, рассмотрим рисунок 1. Пусть тело является материальной точкой, двигающейся только вдоль оси X. В случае, когда угол между векторами и лежит в пределах (рис. 1, а), косинус угла будет положителен , работа силы также положительна:
.
Если сумма остальных сил, действующих на данную материальную точку, равна нулю, то под действием силы тело будет разгоняться.
В противном случае, когда угол тупой (рис. 1, б), косинус данного угла отрицателен , работа силы также будет иметь отрицательное значение:
.
Когда сила совершает отрицательную работу, а сумма других сил, действующих на данное тело, равна нулю, тело приобретает отрицательное ускорение — оно будет тормозить.
Очевидно, что если вектор силы перпендикулярен вектору перемещения , то косинус угла между ними будет равен нулю , в этом случае сила не совершает работу .
Например, на тело, изображённое на рисунке 1, помимо силы действует сила тяжести , направленная под углом 90° к вектору перемещения . Работа силы тяжести при перемещении будет равна нулю.
Заметим, что произведение — это проекция силы на направление перемещения . Можно сказать, что работа силы равна произведению модуля перемещения на проекцию данной силы на направление перемещения.
Пусть на материальную точку действуют две силы и . Под действием этих сил точка совершает перемещение . Вектор перемещения сонаправлен с положительным направлением оси ОХ. Тогда работа силы равна , работа силы вычисляется аналогично .
Известно, что проекция равнодействующей на координатную ось равна сумме проекций всех сил, действующих на тело, на данную ось. Пусть .
Тогда проекция данной силы на ось ОХ равна:
.
Умножим левую и правую часть уравнения на модуль перемещения :
.
Получается, что работа суммы сил и равна сумме работ сил, действующих на тело:
.
Сумма работ всех действующих на материальную точку сил равна работе равнодействующей силы: .
Полученные закономерности справедливы при расчёте работы постоянной силы и постоянного угла между векторами и .
 Рис. 2. Вычисление работы в случае, когда тело было брошено под углом к горизонту
Рис. 2. Вычисление работы в случае, когда тело было брошено под углом к горизонту
Рассмотрим случай, когда направление вектора перемещения , соответственно, и значение угла между векторами и меняется с течением времени.
Например, тело брошено под углом к горизонту (рис. 2). Требуется найти работу силы тяжести по перемещению тела из точки А в точку В.
В данном случае, чтобы вычислить работу, необходимо разбить перемещение материальной точки на достаточно малые перемещения ,, … такие, чтобы на протяжении каждого из данных перемещений модуль силы, совершающей работу, и угол между вектором перемещения и вектором силы можно было считать постоянными.
При выполнении этих условий работу на каждом из участков можно считать по формуле:
.
Полученные значения работ складываются:
.
 Рис. 3. Сила упругости совершает положительную работу
Рис. 3. Сила упругости совершает положительную работу
Рассмотрим ещё один пример.
Пусть пружину жёсткостью сжали на величину (рис. 3). Если перестать удерживать пружину, то под действием силы упругости она вернётся в недеформированное состояние — точку В. Сила упругости при этом совершит работу . Найдём величину этой работы.
Сила упругости, возникающая в пружине, прямо пропорциональна величине , следовательно, по мере движения шарика от точки А к точке В модуль силы упругости будет уменьшаться пропорционально её деформации от максимального значения вплоть до нуля .
На рисунке 4 показана зависимость модуля силы упругости от величины деформации пружины.
Нам уже известно, что, если сила, действующая на тело, изменяется с течением времени, для вычисления работы такой силы перемещение необходимо разбить на достаточно малые промежутки времени, на каждом из которых силу можно считать величиной постоянной.
 Рис. 4. Зависимость модуля силы упругости от величины деформации пружины
Рис. 4. Зависимость модуля силы упругости от величины деформации пружины
Пусть отрезок АВ представляет собой совокупность достаточно малых отрезков , , … и т. д. (рис. 4, а). Тогда модуль силы упругости на отрезке от до можно считать неизменным во времени.
Работа силы упругости на рассматриваемом участке равна . Из рисунка видно, что работа равна площади заштрихованного прямоугольника .
Очевидно, что на каждом достаточно малом участке работа силы упругости будет равна площади соответствующего прямоугольника (рис. 4, б).
Общая работа равна сумме работ на достаточно малых промежутках, следовательно, общая работа равна сумме площадей полученных прямоугольников . Чем больше вводится элементарных отрезков, тем точнее будет вычислена работа силы упругости.
При разбиении на достаточно малые промежутки отрезка АВ сумма площадей всех прямоугольников будет приблизительно равна площади прямоугольного треугольника АВС:
.
Если действующая на материальную точку сила не изменяет своего направления, а сама точка движется в направлении действия силы, то работа этой силы численно равна площади под графиком зависимости модуля силы от модуля перемещения рассматриваемой точки.
Мощность силы
Мощность силы характеризует скорость совершения работы. Например, необходимо поднять холодильник на третий этаж дома. Эту работу можно совершить вручную, используя силу мышц человека, поднявшись по ступеням лестницы. А можно загрузить холодильник в лифт, тогда работу по перемещению холодильника совершит подъёмный механизм лифта, а время совершения работы сократится на несколько минут. Понятно, что разница во времени совершении работы объясняется тем, что подъёмный механизм имеет большую мощность, нежели человек.
Мощность силы — это скалярная физическая величина, характеризующая быстроту совершения работы и равная отношению работы силы , совершённой за достаточно малый промежуток времени , длительности данного промежутка времени: , где .
Единица измерения мощности в СИ — ватт (Вт).
В случае, когда скорость совершения работы в каждый отдельно взятый момент времени не важна, применяется понятие средней мощности.
Средняя мощность — это скалярная физическая величина, равная отношению работы силы к промежутку времени , за который была совершена данная работа: .
Пусть под действием постоянной силы материальная точка движется со скоростью . За достаточно малый промежуток времени точка совершит перемещение . Тогда работа данной силы равна
,
где — угол между направлением вектора и вектора .
Мощность силы в данном случае можно вычислить по следующей формуле:
.
Пример 1
Строитель с помощью верёвки тянет дерево массой 80 кг по земле. Известно, что сила, с которой тянет строитель, направлена под углом к горизонту, а её модуль . За рассматриваемый промежуток времени тело переместилось на м. Определите:
а) работу силы тяжести дерева; б) работу силы трения, действующую на дерево, если коэффициент трения ; в) работу силы тяги.
Решение
1. Воспользуемся рисунком 1 под буквой а) и запишем формулу для работы по определению:
.
Будем использовать эту формулу, подставляя в неё различные силы, указанные в задаче.
2. Начнём с силы тяжести дерева. Поскольку сила тяжести направлена вертикально, а движение происходит в горизонтальном направлении, то работа равна нулю, так как :
.
3. Для определения работы силы трения вспомним формулу для силы трения-скольжения, где в нашей задаче . Сила трения будет направлена противоположно движению, а значит .
.
4. Работы силы тяги:
.
Ответ: ; ; .
Итоги
- Работа постоянной силы — это скалярная физическая величина, равная произведению модуля силы и перемещения тела , умноженному на косинус угла между векторами и : .
- Сумма работ всех действующих на материальную точку сил равна работе равнодействующей силы: .
- Если действующая на материальную точку сила не изменяет своего направления, а сама точка движется в направлении действия силы, то работа этой данной силы численно равна площади под графиком зависимости модуля силы от модуля перемещения рассматриваемой точки.
- Средняя мощность — это скалярная физическая величина, равная отношению работы силы к промежутку времени , за который была совершена данная работа: .
Упражнение 1
1. Груз массой 50 кг тянется по земле под действием силы тяги . Угол между направлением силы тяги и перемещением м равен . Определите работу равнодействующей силы, действующей на груз. Коэффициент трения груза о землю равен .
2. Средняя мощность лифта равна кВт. Какую работу совершит лифт за минуты?
Контрольные вопросы
1. В каком случае работа силы будет отрицательна?
2. Как рассчитать работу силы, если модуль силы изменяется с течением времени?
3. В чём заключается физический смысл мощности?
Упражнение 1
1. 371 Дж
2. 2,1 МДж

