- Центр масс. Теорема о движении центра масс
- Пример решения задачи
- знать понятие «центр масс»; теорему о движении центра масс; формулу для расчёта ускорения центра масс системы
- уметь находить координаты центра масс системы
- Что такое центр масс?
- Как найти центр масс простой геометрической фигуры?
- Как найти координаты центра масс?
Центр масс. Теорема о движении центра масс
Пусть имеется система из 𝑁 материальных точек, массами m1, m2, m3 … mN. Положение данных точек задано радиус-векторами , , … (рис. 1).
Центром масс системы, состоящей из N материальных точек, называется точка, радиус-вектор которой равен отношению суммы произведений массы каждой точки на её радиус-вектор к сумме масс всех точек, входящих в систему:
.
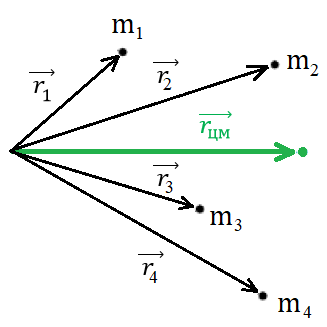 Рис. 1. Система из N материальных точек, положение которых задано радиус-векторами
Рис. 1. Система из N материальных точек, положение которых задано радиус-векторами
Координаты центра масс можно найти по следующим формулам:
;
;
.
Используем эти выражения для определения центра масс системы, состоящей из двух материальных точек, массы которых равны m1 и m2 соответственно. Абсциссы материальных точек равны x1 и x2, точки лежат на оси ОХ (рис. 2).
Из уравнения находим абсциссу центра масс:
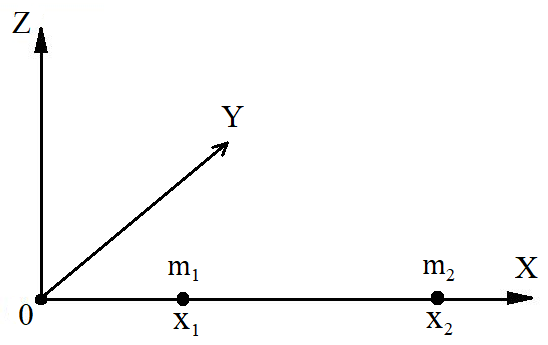 Рис. 2. Определение координаты центра масс системы из двух материальных точек
Рис. 2. Определение координаты центра масс системы из двух материальных точек
.
Так как точки лежат на оси ОХ, оставшиеся координаты центра масс равны нулю: = 0, = 0.
Из уравнения выше понятно, что центр масс данной системы лежит на оси абсцисс между точками с координатами x1 и x2.
В случае, когда массы материальных точек равны m1 = m2, выражение принимает следующий вид:
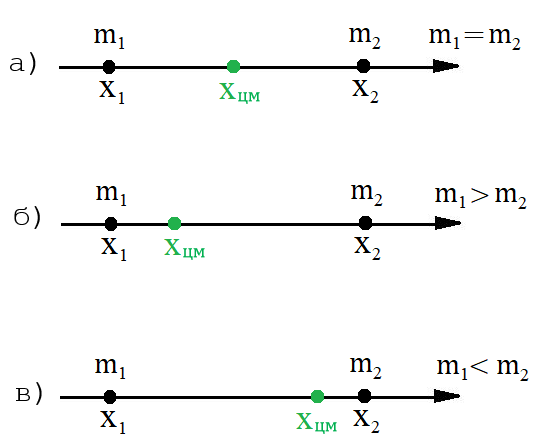 Рис. 3. Положение центра масс двух материальных точек при различных соотношениях их масс
Рис. 3. Положение центра масс двух материальных точек при различных соотношениях их масс
.
Данное выражение показывает, что центр масс двух материальных точек, имеющих одинаковые массы, находится в середине отрезка, соединяющего данные точки (рис. 3, а).
В случае, когда m1 > m2, центр масс будет расположен ближе к материальной точке массой m1 (рис. 3, б); когда m1 < m2, центр масс будет расположен ближе к материальной точке массой m2 (рис. 3, в).
Теорема о движении центра масс: ускорение центра масс системы, которая состоит из N материальных точек, в ИСО равно отношению суммы всех внешних сил, действующих на данные точки, к сумме масс всех материальных точек данной системы:
.
Для доказательства теоремы о движении центра масс рассмотрим достаточно малый промежуток времени Δt, такой, что движение материальной точки на данном отрезке времени можно считать равномерным прямолинейным. Перемещение первой точки, движущейся со скоростью за данный промежуток времени:
.
Перемещение остальных точек системы и центра масс будет ,, …, и соответственно.
Подставим полученные выражения для перемещений в формулу:
.
Сократим обе части уравнения на величину Δt:
.
В течение достаточно малого промежутка времени Δt силы, действующие на каждую из материальных точек системы, можно считать постоянными. Тогда в соответствии с определением изменения импульса для первой точки справедливо следующее равенство:
.
Для остальных материальных точек изменение импульса можно рассчитать аналогичным образом.
В соответствии с уравнением изменение скорости центра масс за промежуток времени Δt равно
.
Подставим в уравнение выше выражения для изменения импульсов материальных точек системы за время Δt, аналогичные выражению . Сумма внутренних сил в числителе правой части уравнения окажется равной нулю в соответствии с третьим законом Ньютона. Полученное выражение разделим на величину Δt, в результате получится следующее выражение:
.
Заметим, что соотношение можно записать в ином виде:
.
Данное выражение показывает, что суммарный импульс системы материальных точек равен произведению суммы масс данных точек на скорость движения центра масс.
Пусть масса всех материальных точек, входящих в систему, равна m, а сумма всех действующих на систему внешних сил равна . Тогда выражение можно записать следующим образом:
.
Это выражение соответствует второму закону Ньютона, описывающему движение материальной точки. Отсюда следует важный вывод.
Любое реальное тело, имеющее конечные размеры, можно представить как совокупность большого количества материальных точек.
Следовательно, к такому телу применима теорема о движении центра масс
,
где — сумма всех внешних сил, действующих на рассматриваемое тело; m — масса тела.
Понятно, что если известны и m, то уравнение выше позволяет рассчитать ускорение центра масс рассматриваемого тела в ИСО. При замене реального тела материальной точкой для решения задач динамики найденное ускорение является ускорением центра масс рассматриваемого тела, а не какой-либо другой его точки.
Подчеркнём, что между взаимодействующими частями тела присутствуют внутренние силы, но их действие не оказывает влияния на ускорение центра масс в ИСО.
Пример решения задачи
Пример
Человек массой m2 = 50 кг стоит на корме лодки массой m1 = 150 кг и длиной L = 10 м. В начальный момент времени лодка находится у пристани, нос лодки совпадает с точкой 0 (рис. 4). Расстояние от носа лодки до её центра масс равно = 6 м. Человек переходит на нос лодки, в результате чего она смещается относительно начальной точки 0. Найти расстояние , на которое сместилась лодка.
Решение
1. Пренебрежём силами сопротивления среды. Инерциальную систему отсчёта свяжем с неподвижной пристанью. Ось ОХ направим горизонтально влево. Человека и лодку представим как систему материальных точек.
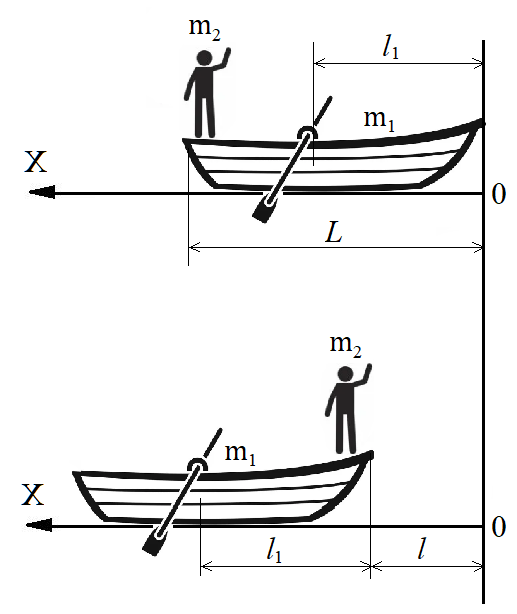 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
2. В начальный момент времени координаты человека и центра масс лодки равны соответственно L и . Используя соотношение, найдём координату центра масс системы в начальный момент времени:
.
После того как человек переместился на нос лодки, его координата стала равна , а координата центра масс лодки — . По формуле находим координату центра масс системы в конечный момент времени:
.
3. Так как внешние силы сопротивления среды в системе отсутствуют, в соответствии с уравнением ускорение центра масс системы равно нулю. Следовательно, положение центра масс остаётся неизменным:
.
4. Подставляем в выражение выше уравнения и выражаем расстояние , на которое сместилась лодка:
;
.
Ответ: .
Итоги
- Центром масс системы, состоящей из N материальных точек, называется точка, радиус-вектор которой равен отношению суммы произведений массы каждой точки на её радиус-вектор к сумме масс всех точек, входящих в систему: .
- Теорема о движении центра масс: ускорение центра масс системы, которая состоит из N материальных точек, в ИСО равно отношению суммы всех внешних сил, действующих на данные точки, к сумме масс всех материальных точек данной системы: .
- Любое реальное тело, имеющее конечные размеры, можно представить как совокупность большого количества материальных точек.
Контрольные вопросы
1. Как найти положение центра масс системы материальных точек?
2. Сформулируйте теорему о движении центра масс.
3. В каком случае ускорение центра масс системы материальных точек равно нулю?
- Центр масс. Теорема о движении центра масс
- Пример решения задачи
- знать понятие «центр масс»; теорему о движении центра масс; формулу для расчёта ускорения центра масс системы
- уметь находить координаты центра масс системы
- Что такое центр масс?
- Как найти центр масс простой геометрической фигуры?
- Как найти координаты центра масс?
Центр масс. Теорема о движении центра масс
Пусть имеется система из 𝑁 материальных точек, массами m1, m2, m3 … mN. Положение данных точек задано радиус-векторами , , … (рис. 1).
Центром масс системы, состоящей из N материальных точек, называется точка, радиус-вектор которой равен отношению суммы произведений массы каждой точки на её радиус-вектор к сумме масс всех точек, входящих в систему:
.
 Рис. 1. Система из N материальных точек, положение которых задано радиус-векторами
Рис. 1. Система из N материальных точек, положение которых задано радиус-векторами
Координаты центра масс можно найти по следующим формулам:
;
;
.
Используем эти выражения для определения центра масс системы, состоящей из двух материальных точек, массы которых равны m1 и m2 соответственно. Абсциссы материальных точек равны x1 и x2, точки лежат на оси ОХ (рис. 2).
Из уравнения находим абсциссу центра масс:
 Рис. 2. Определение координаты центра масс системы из двух материальных точек
Рис. 2. Определение координаты центра масс системы из двух материальных точек
.
Так как точки лежат на оси ОХ, оставшиеся координаты центра масс равны нулю: = 0, = 0.
Из уравнения выше понятно, что центр масс данной системы лежит на оси абсцисс между точками с координатами x1 и x2.
В случае, когда массы материальных точек равны m1 = m2, выражение принимает следующий вид:
 Рис. 3. Положение центра масс двух материальных точек при различных соотношениях их масс
Рис. 3. Положение центра масс двух материальных точек при различных соотношениях их масс
.
Данное выражение показывает, что центр масс двух материальных точек, имеющих одинаковые массы, находится в середине отрезка, соединяющего данные точки (рис. 3, а).
В случае, когда m1 > m2, центр масс будет расположен ближе к материальной точке массой m1 (рис. 3, б); когда m1 < m2, центр масс будет расположен ближе к материальной точке массой m2 (рис. 3, в).
Теорема о движении центра масс: ускорение центра масс системы, которая состоит из N материальных точек, в ИСО равно отношению суммы всех внешних сил, действующих на данные точки, к сумме масс всех материальных точек данной системы:
.
Для доказательства теоремы о движении центра масс рассмотрим достаточно малый промежуток времени Δt, такой, что движение материальной точки на данном отрезке времени можно считать равномерным прямолинейным. Перемещение первой точки, движущейся со скоростью за данный промежуток времени:
.
Перемещение остальных точек системы и центра масс будет ,, …, и соответственно.
Подставим полученные выражения для перемещений в формулу:
.
Сократим обе части уравнения на величину Δt:
.
В течение достаточно малого промежутка времени Δt силы, действующие на каждую из материальных точек системы, можно считать постоянными. Тогда в соответствии с определением изменения импульса для первой точки справедливо следующее равенство:
.
Для остальных материальных точек изменение импульса можно рассчитать аналогичным образом.
В соответствии с уравнением изменение скорости центра масс за промежуток времени Δt равно
.
Подставим в уравнение выше выражения для изменения импульсов материальных точек системы за время Δt, аналогичные выражению . Сумма внутренних сил в числителе правой части уравнения окажется равной нулю в соответствии с третьим законом Ньютона. Полученное выражение разделим на величину Δt, в результате получится следующее выражение:
.
Заметим, что соотношение можно записать в ином виде:
.
Данное выражение показывает, что суммарный импульс системы материальных точек равен произведению суммы масс данных точек на скорость движения центра масс.
Пусть масса всех материальных точек, входящих в систему, равна m, а сумма всех действующих на систему внешних сил равна . Тогда выражение можно записать следующим образом:
.
Это выражение соответствует второму закону Ньютона, описывающему движение материальной точки. Отсюда следует важный вывод.
Любое реальное тело, имеющее конечные размеры, можно представить как совокупность большого количества материальных точек.
Следовательно, к такому телу применима теорема о движении центра масс
,
где — сумма всех внешних сил, действующих на рассматриваемое тело; m — масса тела.
Понятно, что если известны и m, то уравнение выше позволяет рассчитать ускорение центра масс рассматриваемого тела в ИСО. При замене реального тела материальной точкой для решения задач динамики найденное ускорение является ускорением центра масс рассматриваемого тела, а не какой-либо другой его точки.
Подчеркнём, что между взаимодействующими частями тела присутствуют внутренние силы, но их действие не оказывает влияния на ускорение центра масс в ИСО.
Пример решения задачи
Пример
Человек массой m2 = 50 кг стоит на корме лодки массой m1 = 150 кг и длиной L = 10 м. В начальный момент времени лодка находится у пристани, нос лодки совпадает с точкой 0 (рис. 4). Расстояние от носа лодки до её центра масс равно = 6 м. Человек переходит на нос лодки, в результате чего она смещается относительно начальной точки 0. Найти расстояние , на которое сместилась лодка.
Решение
1. Пренебрежём силами сопротивления среды. Инерциальную систему отсчёта свяжем с неподвижной пристанью. Ось ОХ направим горизонтально влево. Человека и лодку представим как систему материальных точек.
 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
2. В начальный момент времени координаты человека и центра масс лодки равны соответственно L и . Используя соотношение, найдём координату центра масс системы в начальный момент времени:
.
После того как человек переместился на нос лодки, его координата стала равна , а координата центра масс лодки — . По формуле находим координату центра масс системы в конечный момент времени:
.
3. Так как внешние силы сопротивления среды в системе отсутствуют, в соответствии с уравнением ускорение центра масс системы равно нулю. Следовательно, положение центра масс остаётся неизменным:
.
4. Подставляем в выражение выше уравнения и выражаем расстояние , на которое сместилась лодка:
;
.
Ответ: .
Итоги
- Центром масс системы, состоящей из N материальных точек, называется точка, радиус-вектор которой равен отношению суммы произведений массы каждой точки на её радиус-вектор к сумме масс всех точек, входящих в систему: .
- Теорема о движении центра масс: ускорение центра масс системы, которая состоит из N материальных точек, в ИСО равно отношению суммы всех внешних сил, действующих на данные точки, к сумме масс всех материальных точек данной системы: .
- Любое реальное тело, имеющее конечные размеры, можно представить как совокупность большого количества материальных точек.
Контрольные вопросы
1. Как найти положение центра масс системы материальных точек?
2. Сформулируйте теорему о движении центра масс.
3. В каком случае ускорение центра масс системы материальных точек равно нулю?

