Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
10 класс
Физика
Кинетическая энергия. Потенциальная энергия

Физика 10 класс Физика 10 класс

Конспект урока: Кинетическая энергия. Потенциальная энергия

Законы сохранения в механике

14.02.2025

2879

Кинетическая энергия

План урока

Кинетическая энергия
Пример решения задачи

Цели урока

знать формулу и физический смысл кинетической энергии; теорему об изменении кинетической энергии
уметь находить кинетическую энергию движущегося тела; выводить и использовать теорему об изменении кинетической энергии тела

Разминка

Как изменится скорость тела, если совершить над ним положительную работу?
Как изменится скорость тела, если работа силы, приложенной к телу, равна нулю?
По какой формуле рассчитывается работа силы?

Кинетическая энергия

Известно, что при совершении положительной работы над материальной точкой её скорость увеличивается, при совершении отрицательной работы — уменьшается. Определим математическую связь между работой и изменением скорости тела.

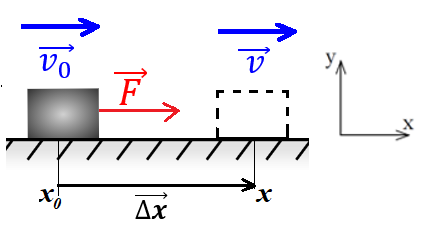Рис. 1. Сила F совершает положительную работу над телом

Пусть тело массой $m$ движется в положительном направлении оси ОХ (рис. 1). Начальная скорость тела равна ${\vec{v}}_{0}$ .

На тело начинает действовать постоянная сила $\vec{F}$ , сонаправленная с вектором перемещения $∆ \vec{x}$ . В данном случае сила совершает положительную работу, следовательно, тело приобретёт некоторое положительное ускорение, которое можно найти по второму закону Ньютона:

$a = \frac{F}{m}$ .

Скорость тела через время $t$ можно найти по закону изменения скорости для равноускоренного движения:

$\vec{v} = {\vec{v}}_{0} + \vec{a} \cdot t$ .

Запишем данное выражение в проекциях на ось ОХ:

$v = v_{0} + a \cdot t$ .

Проекция модуля перемещения тела на ось ОХ за время $t$ :

$∆ x = v_{0} \cdot t + \frac{a \cdot t^{2}}{2}$ .

Выразим из формулы $v = v_{0} + a \cdot t$ время $t$ и подставим полученное выражение в формулу выше:

$∆ x = v_{0} \cdot (\frac{v - v_{0}}{a}) + \frac{a \cdot {(v - v_{0})}^{2}}{2 a^{2}} = \frac{v_{0} \cdot 2 a \cdot (v - v_{0})}{2 a^{2}} + \frac{a \cdot {(v - v_{0})}^{2}}{2 a^{2}} = \frac{v^{2} - v_{0}^{2}}{2 a}$ .

Умножим обе части уравнения на $F$ и учтём, что по второму закону Ньютона $F = m \cdot a$ :

$F \cdot ∆ x = F \cdot \frac{v^{2} - v_{0}^{2}}{2 a} \Leftrightarrow A = m \cdot a \cdot \frac{v^{2} - v_{0}^{2}}{2 a} \Leftrightarrow A = \frac{m \cdot v^{2}}{2} - \frac{m \cdot v_{0}^{2}}{2}$ .

Физическая величина, равная $\frac{m \cdot v^{2}}{2}$ называется кинетической энергией тела $E_{кин}$ :

$E_{кин} = \frac{m \cdot v^{2}}{2}$ ,

где $E_{кин}$ [Дж] — кинетическая энергия тела;
$m$ [кг] — масса тела;
$v$ [м/с] — скорость тела в инерциальной системе отсчёта.

Кинетическая энергия тела $E_{кин}$ — это физическая величина, равная половине произведения массы тела на квадрат его скорости в ИСО: $E_{кин} = \frac{m \cdot v^{2}}{2}$ .

Таким образом, работа, совершённая над телом, равна изменению его кинетической энергии в инерциальной системе отсчёта:

$A = E_{кин} - E_{кин 0} = ∆ E_{кин}$ .

Это соотношение выполняется не только в случае прямолинейного движения под действием постоянной силы $\vec{F}$ , но и в случае, если траектория тела криволинейная, а сила $\vec{F}$ изменяется с течением времени.

Теорема об изменении кинетической энергии
Изменение кинетической энергии материальной точки в ИСО при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении: $A = ∆ E_{кин}$ .

Теорема об изменении кинетической энергии позволяет выяснить, в чём заключается физический смысл кинетической энергии. Пусть материальная точка покоится в инерциальной системе отсчёта. В этом случае её начальная кинетическая энергия также равна нулю $E_{кин 0} = 0$ . При совершении над материальной точкой работы $A$ её кинетическая энергия будет равна совершённой работе:

$A = E_{кин} - E_{кин 0} = E_{кин} = \frac{m \cdot v^{2}}{2}$ .

Кинетическая энергия материальной точки равна работе $A$ , которую необходимо совершить, чтобы увеличить скорость материальной точки от нуля до значения $v$ .

Справедливо и обратное утверждение. Если в инерциальной системе отсчёта материальная точка имеет некоторую скорость $v$ , то при совершении над точкой отрицательной работы $A$ , равной её начальной кинетической энергии, конечная кинетическая энергия данной точки станет равна нулю. В процессе торможения материальная точка совершит положительную работу, равную по модулю работе тормозящих сил.

Кинетическая энергия материальной точки равна работе $A$ , которую она может совершить над другими телами при уменьшении своей скорости от некоторого значения $v$ до нуля.

Рассмотрим систему материальных точек, имеющих скорости, отличные от нуля. Кинетические энергии точек равны соответственно ${E_{кин}}_{1} = \frac{m_{1} \cdot v_{1}^{2}}{2}$ , ${E_{кин}}_{2} = \frac{m_{2} \cdot v_{2}^{2}}{2}$ … ${E_{кин}}_{n} = \frac{m_{n} \cdot v_{n}^{2}}{2}$ . Каждая из этих точек при уменьшении своей скорости до нуля сможет совершить работу, равную её кинетической энергии: $A_{1} = E_{кин 1}$ , $A_{2} = E_{кин 2}$ … $A_{n} = E_{кин n}$ . Тогда система материальных точек совершит работу

$A = A_{1} + A_{2} + . . . + A_{n} = E_{кин 1} + E_{кин 2} + . . . + E_{кин n}$ .

Таким образом, работа системы материальных точек равна сумме кинетических энергий всех точек системы.

Кинетическая энергия системы материальных точек равна сумме их кинетических энергий: $E_{кин} = E_{кин 1} + E_{кин 2} + . . . + E_{кин n}$ .

Пример решения задачи

С крыши дома высотой $h$ = 100 м вертикально вниз со скоростью 20 м/с бросают камень. Найти скорость камня в момент падения на Землю.

Решение

1. Примем рассматриваемое тело за материальную точку. Систему отсчёта свяжем с Землёй.

2. Работа силы тяжести $m \cdot \vec{g}$ , под действием которой падает камень, по определению равна произведению модуля силы на модуль перемещения и на косинус угла между векторами $m \cdot \vec{g}$ и $∆ \vec{x}$ :

$A = m \cdot g \cdot ∆ x \cdot \cos (α)$ .

В нашем случае перемещение камня равно высоте, с которой он падает, а угол между вектором силы и вектором перемещения составляет 0°. Тогда выражение выше принимает следующий вид:

$A = m \cdot g \cdot h \cdot \cos (0 °) = m \cdot g \cdot h$ .

3. По теореме о кинетической энергии работа, совершённая над телом, равна изменению кинетической энергии тела:

$A = E_{кин} - E_{кин 0} = \frac{m \cdot v^{2}}{2} - \frac{m \cdot v_{0}^{2}}{2}$ .

4. Приравниваем выражения и выражаем искомую скорость:

$m \cdot g \cdot h = \frac{m \cdot v^{2}}{2} - \frac{m \cdot v_{0}^{2}}{2}$ ;

$v = \sqrt[2]{2 g \cdot h + v_{0}^{2}} = \sqrt[2]{2 \cdot 10 \cdot 100 + 20^{2}} \approx 49 м / с$ .

Ответ: $v = 49 м / с$ .

Итоги

Кинетическая энергия тела $E_{кин}$ — это физическая величина, равная половине произведения массы тела на квадрат его скорости в ИСО: $E_{кин} = \frac{m \cdot v^{2}}{2}$ .
Кинетическая энергия материальной точки равна работе $A$ , которую необходимо совершить, чтобы увеличить скорость материальной точки от нуля до значения $v$ .
Кинетическая энергия материальной точки равна работе $A$ , которую она может совершить над другими телами при уменьшении своей скорости от некоторого значения $v$ до нуля.
Теорема о кинетической энергии: изменение кинетической энергии материальной точки в ИСО при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении: $A = ∆ E_{кин}$ .
Кинетическая энергия системы материальных точек равна сумме их кинетических энергий: $E_{кин} = E_{кин 1} + E_{кин 2} + . . . + E_{кин n}$ .

Упражнение 1

1. Определите кинетическую энергию мяча массой 700 г, который летит в воздухе со скоростью 15 м/с.

2. Пуля массой 15 г летит в горизонтальном направлении со скоростью 300 м/с и пробивает насквозь фанеру толщиной 1 см. Определите среднюю силу сопротивления фанеры, если пуля вылетела со скоростью 200 м/с.

Контрольные вопросы

1. Как изменится кинетическая энергия материальной точки, если совершить над ней отрицательную работу?
2. Сформулируйте теорему об изменении кинетической энергии.
3. В чём заключается физический смысл кинетической энергии?

Ответы

Упражнение 1

1. $E_{к и н} \approx 79$ Дж

2. $37, 5$ кН

Предыдущий урок

Решение задач с использованием законов сохранения импульса и механической энергии

Законы сохранения в механике

Следующий урок

Механическая энергия системы тел. Изменение механической энергии. Закон сохранения механической энергии

Законы сохранения в механике

Урок подготовил(а)