- Механическая энергия системы тел. Закон изменения механической энергии. Закон сохранения механической энергии
- Пример решения задачи на закон сохранения энергии
- знать понятие «механическая энергия системы тел»; законы сохранения и изменения механической энергии системы
- уметь применять законы сохранения и изменения механической энергии системы при решении задач
- Как рассчитывается потенциальная энергия тела в поле тяжести Земли?
- Как рассчитывается кинетическая энергия тела?
- Как изменяется потенциальная энергия тела, брошенного под углом к горизонту, в процессе движения?
Механическая энергия системы тел. Закон изменения механической энергии. Закон сохранения механической энергии
Вам уже известно, что кинетическая и потенциальная энергии характеризуют механическое состояние тела или системы тел.
Механическая энергия системы тел (тела) — это сумма кинетической и потенциальной энергии системы (тела): .
Пусть работа всех сил, действующих на материальную точку, равна . Тогда в соответствии с теоремой о кинетической энергии справедливо следующее выражение:
,
где работа всех сил представляет собой сумму работы внутренних потенциальных сил , работы внутренних сил трения и работы внешних сил :
.
С учётом выражения выше формула принимает следующий вид:
.
Работа потенциальных сил равна изменению потенциальной энергии системы, взятой со знаком минус:
.
Подставим это уравнение в формулу :
.
Запишем полученное выражение иначе:
.
Механическая энергия системы — это сумма кинетической и потенциальной энергии системы, тогда начальная и конечная механические энергии системы соответственно равны:
и .
Тогда выражение можно записать в следующем виде:
.
Формула выше говорит о том, что механическая энергия системы изменится только при совершении работы внутренними силами трения или в случае совершения работы над телами системы внешними силами.
Закон изменения механической энергии системы тел
Изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
Заметим, что закон изменения механической энергии системы тел применим только в инерциальных системах отсчёта.
Закон сохранения механической энергии является следствием закона изменения механической энергии.
Закон сохранения механической энергии системы тел
Если сумма работ внутренних сил трения и внешних сил над телами системы равна нулю, то механическая энергия системы не изменяется: при .
Пример решения задачи на закон сохранения энергии
Пример 1
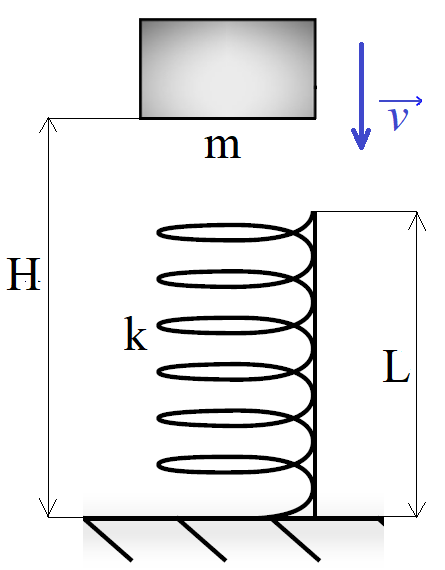 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
Пружина жёсткостью = 200 Н/м вертикально стоит на горизонтальной площадке. С высоты
= 50 м на пружину свободно падает брусок массой = 2 кг (рис. 1).
Определите максимальную скорость бруска при его движении вниз после приземления на пружину, если первоначальная длина пружины см. Потерями энергии на трение пренебречь.
Решение
1. Примем брусок за материальную точку. Инерциальную систему отсчёта свяжем с Землёй.
2. Брусок падает под действием силы тяжести , помимо этого, в момент касания бруском пружины на него начнет действовать сила упругости. Модуль силы упругости по мере движения бруска будет увеличиваться. Брусок будет продолжат разгоняться до тех пор, пока модуль силы тяжести больше модуля силы упругости. Когда модуль силы упругости окажется больше модуля силы тяжести, брусок начнёт терять скорость.
Следовательно, скорость бруска будет максимальна в тот момент, когда действующие на него силы будут равны друг другу по модулю:
,
где — величина сжатия пружины в соответствующий момент времени.
3. Оценим кинетическую и потенциальную энергии бруска в начальный момент времени и в момент, когда будет достигнута максимальная скорость:
;
.
В начальный момент времени брусок находился на высоте , следовательно, начальная потенциальная энергия системы равна
.
В момент, когда будет достигнута максимальная скорость, брусок будет находиться на высоте . Помимо этого, пружина сжимается на величину , поэтому система «брусок – пружина» будет обладать и потенциальной энергией в поле тяжести Земли, и потенциальной энергией упруго деформированной пружины:
.
4. Так как в рассматриваемой задаче трения в системе нет и отсутствуют внешние силы , применим закон сохранения энергии:
.
Подставим в закон сохранения механической энергии полученные выражения для кинетических и потенциальных энергий:
.
Используем соотношение , чтобы исключить неизвестную величину :
.
Подставим полученное выражение в формулу и выразим искомую скорость:
;
.
Ответ: .
Итоги
- Механическая энергия системы тел — это сумма кинетической и потенциальной энергии системы: .
- Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
- Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения и внешних сил над телами системы равна нулю, то механическая энергия системы не изменяется: при .
Упражнение 1
1. На какой высоте кинетическая энергия будет в 2 раза больше потенциальной, если тело брошено вертикально вверх с поверхности Земли со скоростью 50 м/с?
2. При подготовке пружинного пистолета к выстрелу пружину жёсткостью 1 кН/м сжали на 5 см. Какую скорость приобретёт пуля массой 150 г в момент выстрела? Потерями энергии пренебречь.
3. С крыши многоэтажного дома высотой 100 м бросили камень под углом 30° к горизонту с начальной скоростью 5 м/с. Найти модуль конечной скорости камня при его приземлении на Землю. Потерями энергии пренебречь.
Контрольные вопросы
1. Как рассчитывается механическая энергия системы тел?
2. Сформулируйте закон изменения механической энергии.
3. Сформулируйте закон сохранения механической энергии.
Упражнение 1
1. = 41,7 м
2. = 4 м/с
3. = 45 м/с
- Механическая энергия системы тел. Закон изменения механической энергии. Закон сохранения механической энергии
- Пример решения задачи на закон сохранения энергии
- знать понятие «механическая энергия системы тел»; законы сохранения и изменения механической энергии системы
- уметь применять законы сохранения и изменения механической энергии системы при решении задач
- Как рассчитывается потенциальная энергия тела в поле тяжести Земли?
- Как рассчитывается кинетическая энергия тела?
- Как изменяется потенциальная энергия тела, брошенного под углом к горизонту, в процессе движения?
Механическая энергия системы тел. Закон изменения механической энергии. Закон сохранения механической энергии
Вам уже известно, что кинетическая и потенциальная энергии характеризуют механическое состояние тела или системы тел.
Механическая энергия системы тел (тела) — это сумма кинетической и потенциальной энергии системы (тела): .
Пусть работа всех сил, действующих на материальную точку, равна . Тогда в соответствии с теоремой о кинетической энергии справедливо следующее выражение:
,
где работа всех сил представляет собой сумму работы внутренних потенциальных сил , работы внутренних сил трения и работы внешних сил :
.
С учётом выражения выше формула принимает следующий вид:
.
Работа потенциальных сил равна изменению потенциальной энергии системы, взятой со знаком минус:
.
Подставим это уравнение в формулу :
.
Запишем полученное выражение иначе:
.
Механическая энергия системы — это сумма кинетической и потенциальной энергии системы, тогда начальная и конечная механические энергии системы соответственно равны:
и .
Тогда выражение можно записать в следующем виде:
.
Формула выше говорит о том, что механическая энергия системы изменится только при совершении работы внутренними силами трения или в случае совершения работы над телами системы внешними силами.
Закон изменения механической энергии системы тел
Изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
Заметим, что закон изменения механической энергии системы тел применим только в инерциальных системах отсчёта.
Закон сохранения механической энергии является следствием закона изменения механической энергии.
Закон сохранения механической энергии системы тел
Если сумма работ внутренних сил трения и внешних сил над телами системы равна нулю, то механическая энергия системы не изменяется: при .
Пример решения задачи на закон сохранения энергии
Пример 1
 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
Пружина жёсткостью = 200 Н/м вертикально стоит на горизонтальной площадке. С высоты
= 50 м на пружину свободно падает брусок массой = 2 кг (рис. 1).
Определите максимальную скорость бруска при его движении вниз после приземления на пружину, если первоначальная длина пружины см. Потерями энергии на трение пренебречь.
Решение
1. Примем брусок за материальную точку. Инерциальную систему отсчёта свяжем с Землёй.
2. Брусок падает под действием силы тяжести , помимо этого, в момент касания бруском пружины на него начнет действовать сила упругости. Модуль силы упругости по мере движения бруска будет увеличиваться. Брусок будет продолжат разгоняться до тех пор, пока модуль силы тяжести больше модуля силы упругости. Когда модуль силы упругости окажется больше модуля силы тяжести, брусок начнёт терять скорость.
Следовательно, скорость бруска будет максимальна в тот момент, когда действующие на него силы будут равны друг другу по модулю:
,
где — величина сжатия пружины в соответствующий момент времени.
3. Оценим кинетическую и потенциальную энергии бруска в начальный момент времени и в момент, когда будет достигнута максимальная скорость:
;
.
В начальный момент времени брусок находился на высоте , следовательно, начальная потенциальная энергия системы равна
.
В момент, когда будет достигнута максимальная скорость, брусок будет находиться на высоте . Помимо этого, пружина сжимается на величину , поэтому система «брусок – пружина» будет обладать и потенциальной энергией в поле тяжести Земли, и потенциальной энергией упруго деформированной пружины:
.
4. Так как в рассматриваемой задаче трения в системе нет и отсутствуют внешние силы , применим закон сохранения энергии:
.
Подставим в закон сохранения механической энергии полученные выражения для кинетических и потенциальных энергий:
.
Используем соотношение , чтобы исключить неизвестную величину :
.
Подставим полученное выражение в формулу и выразим искомую скорость:
;
.
Ответ: .
Итоги
- Механическая энергия системы тел — это сумма кинетической и потенциальной энергии системы: .
- Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
- Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения и внешних сил над телами системы равна нулю, то механическая энергия системы не изменяется: при .
Упражнение 1
1. На какой высоте кинетическая энергия будет в 2 раза больше потенциальной, если тело брошено вертикально вверх с поверхности Земли со скоростью 50 м/с?
2. При подготовке пружинного пистолета к выстрелу пружину жёсткостью 1 кН/м сжали на 5 см. Какую скорость приобретёт пуля массой 150 г в момент выстрела? Потерями энергии пренебречь.
3. С крыши многоэтажного дома высотой 100 м бросили камень под углом 30° к горизонту с начальной скоростью 5 м/с. Найти модуль конечной скорости камня при его приземлении на Землю. Потерями энергии пренебречь.
Контрольные вопросы
1. Как рассчитывается механическая энергия системы тел?
2. Сформулируйте закон изменения механической энергии.
3. Сформулируйте закон сохранения механической энергии.
Упражнение 1
1. = 41,7 м
2. = 4 м/с
3. = 45 м/с

