- Основные формулы
- Примеры решения задач
- знать основные формулы для законов сохранения импульса и механической энергии
- уметь применять закон сохранения импульса
- уметь применять закон сохранения энергии
- Какие тела обладают кинетической энергией?
- Что называют импульсом тела?
- Какие удары называются упругими, а какие абсолютно неупругими?
Основные формулы
Перечислим основные формулы и законы, которые нам понадобятся для решения задач с использованием законов сохранения импульса и механической энергии.
- Импульс тела:
.
- Закон сохранения импульса при абсолютно упругом ударе двух тел:
.
- Закон сохранения импульса при неупругом ударе двух тел:
.
- Кинетическая энергия тела, двигающегося со скоростью :
.
- Потенциальная энергия тела, поднятого над поверхностью Земли на высоту :
.
- Потенциальная энергия упруго деформированной пружины, растянутой или сжатой на расстояние от положения равновесия:
.
- Закон изменения полной механической энергии системы тел:
,
где — сумма работ внутренних сил трения и внешних сил над телами системы; и — конечная и начальная механические энергии системы тел соответственно.
- В случае когда суммарная работа внутренних сил трения и внешних сил над телами системы равна нулю, механическая энергия сохраняется:
;
.
Примеры решения задач
Пример 1
Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жёстком стержне, и застревает в нём. Масса пули = 8 г, масса шара = 0,9 кг. Скорость пули = 400 м/с. При каком предельном расстоянии от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?
Решение
1. Перечислим исходные данные:
.
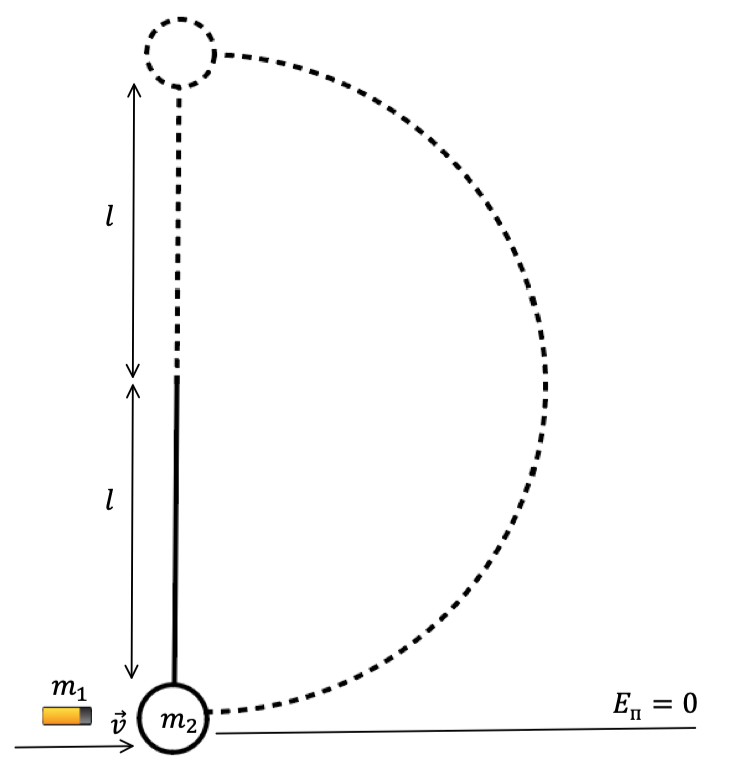 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
2. Примем рассматриваемые тела за материальные точки, а инерциальную систему отсчёта свяжем с Землёй. Рассмотрим, как будет происходить физический процесс (см. рис. 1). Пуля летит, попадает в шар, происходит неупругий удар. Теперь приходит в движение система «шар + пуля», траектория движения которой представляет собой дугу окружности.
3. Зададимся вопросом, какие физические законы следует применить для решения задачи. Чтобы понять, с какой скоростью начнёт двигаться система «шар + пуля» сразу после столкновения, применим закон сохранения импульса для неупругого удара:
.
Направим ось OX горизонтально вправо и спроецируем скорости:
.
Выразим скорость системы «шар + пуля»:
.
4. В результате столкновения пули с шаром система приобретает кинетическую энергию, которая в наивысшей точке движения перейдёт полностью в потенциальную. На рисунке отмечен нулевой уровень потенциальной энергии. Тогда в наивысшей точке система «шар + пуля» будет иметь потенциальную энергию
.
Воспользуемся законом сохранения энергии для системы «шар + пуля»:
.
Подставим формулу в выражение выше и выразим оттуда :
;
5. Найдём численное значение:
.
Ответ: .
Пример 2
Разберём качественную задачу, решение которой будет полезно при решении задач на законы сохранения. Два шара массами , двигаются навстречу друг другу со скоростями , в горизонтальном направлении. Определить скорости шаров в результате центрального абсолютно упругого удара.
Решение
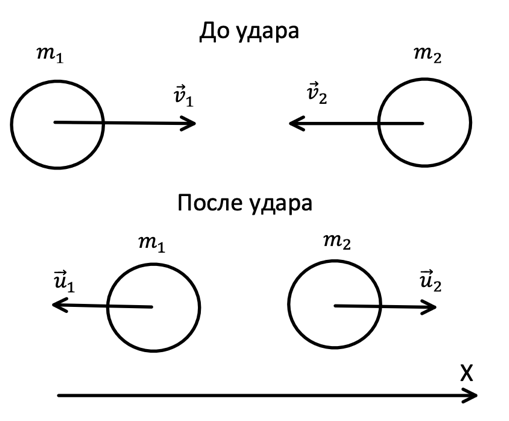 Рис. 2. Иллюстрация к примеру
Рис. 2. Иллюстрация к примеру
1. Первым делом разберёмся с терминологией. Абсолютно упругий удар — это такой удар, в результате которого механическая энергия тел не переходит в другие виды энергии, то есть энергия сохраняется. А центральный удар — это удар, при котором тела двигаются вдоль линии, соединяющей центры масс этих тел. Рассмотрим случай, в котором шары после удара разлетелись в противоположные стороны.
2. Будем предполагать, что шары образуют замкнутую систему. Тогда для центрального абсолютно упругого удара выполняются закон сохранения импульса (ЗСИ) и закон сохранения энергии (ЗСЭ).
Начнём с ЗСИ:
.
Спроецируем скорости на ось ОХ:
.
Запишем ЗСЭ:
.
3. Наша задача — решить систему уравнений относительно величин и .
.
Преобразуем систему:
,
.
Поделим второе уравнение системы на первое:
.
Теперь рассмотрим новую систему, которая легко решается:
.
4. После небольших преобразований получаем выражения для скоростей:
.
5. Из анализов конечного результата можно заметить, что если массы шаров одинаковы, то тела просто обмениваются скоростями:
;
.
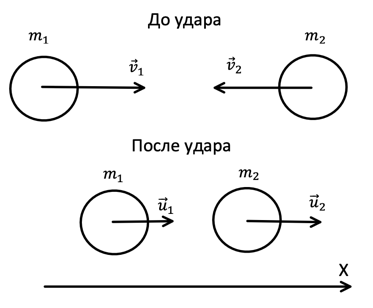 Рис. 3. Иллюстрация к примеру
Рис. 3. Иллюстрация к примеру
6. Возможна ситуация, когда шары после удара двигаются в одном направлении.
Решение такой задачи аналогично предыдущей, но с учётом новых проекций скоростей.
При абсолютно неупругом ударе закон сохранения импульса выполняется, а закон сохранения энергии — нет. Энергия может выделиться в виде теплоты или пойти на изменение внутренней энергии тел.
В случае абсолютно упругого удара выполняется как закон сохранения импульса, так и закон сохранения энергии.
Пример 3
На столе лежит невесомая пружина жёсткостью 1 кН/м, прикреплённая одним концом к грузу массой 0,2 кг, а другим к стене. Груз сдвигают, сжимая пружину, и отпускают. Найдите длину, на которую сжали пружину, если после отпускания груза его скорость достигла величины 3 м/с. Трением пренебречь.
Решение
1. Перечислим исходные данные:
.
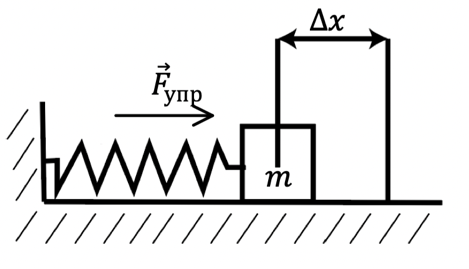 Рис. 4. Иллюстрация к примеру
Рис. 4. Иллюстрация к примеру
2. Как только мы сожмём пружину, так сразу же в ней возникнет сила упругости, которая захочет вернуть пружину в исходное положение. По условию трением следует пренебречь, тогда система начнёт совершать гармонические колебания, во время которых энергия будет переходить из потенциальной в кинетическую. Момент, когда пружина сжата, изображён на рисунке 4.
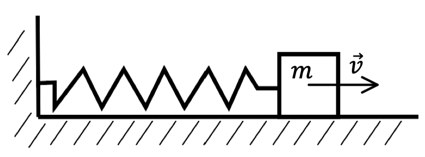 Рис. 5. Иллюстрация к примеру
Рис. 5. Иллюстрация к примеру
Как только мы отпустим груз, так сразу пружина придёт в движение, и проходя положение равновесия, груз достигнет максимальной скорости (рис. 5).
3. Сила тяжести и сила реакции опоры направлены перпендикулярно направлению движения. Рассмотрим замкнутую систему «груз + пружина», для которой в отсутствие сил трения будет выполняться закон сохранения энергия:
.
Выразим отсюда :
.
Ответ: .
Упражнение 1
1. Груз массой 0,4 кг падает с некоторой высоты на подложку массой 2 кг, закреплённую на пружине. Определите наибольшее сжатие пружины, если в момент удара скорость груза равнялась 8 м/с. Жёсткость пружины = 1 кН/м.
2. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жёстком стержне, и застревает в нём. Масса пули в 800 раз меньше массы шара. Расстояние от точки подвеса стержня до центра 2 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 7°.
Контрольные вопросы
1. Как выглядит закон сохранения импульса при неупругом ударе?
2. Что такое центральный удар?
3. Что называют полной механической энергией?
Упражнение 1
1. ≈ 9,3 см
2. ≈ 437 м/с
- Основные формулы
- Примеры решения задач
- знать основные формулы для законов сохранения импульса и механической энергии
- уметь применять закон сохранения импульса
- уметь применять закон сохранения энергии
- Какие тела обладают кинетической энергией?
- Что называют импульсом тела?
- Какие удары называются упругими, а какие абсолютно неупругими?
Основные формулы
Перечислим основные формулы и законы, которые нам понадобятся для решения задач с использованием законов сохранения импульса и механической энергии.
- Импульс тела:
.
- Закон сохранения импульса при абсолютно упругом ударе двух тел:
.
- Закон сохранения импульса при неупругом ударе двух тел:
.
- Кинетическая энергия тела, двигающегося со скоростью :
.
- Потенциальная энергия тела, поднятого над поверхностью Земли на высоту :
.
- Потенциальная энергия упруго деформированной пружины, растянутой или сжатой на расстояние от положения равновесия:
.
- Закон изменения полной механической энергии системы тел:
,
где — сумма работ внутренних сил трения и внешних сил над телами системы; и — конечная и начальная механические энергии системы тел соответственно.
- В случае когда суммарная работа внутренних сил трения и внешних сил над телами системы равна нулю, механическая энергия сохраняется:
;
.
Примеры решения задач
Пример 1
Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жёстком стержне, и застревает в нём. Масса пули = 8 г, масса шара = 0,9 кг. Скорость пули = 400 м/с. При каком предельном расстоянии от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?
Решение
1. Перечислим исходные данные:
.
 Рис. 1. Иллюстрация к примеру
Рис. 1. Иллюстрация к примеру
2. Примем рассматриваемые тела за материальные точки, а инерциальную систему отсчёта свяжем с Землёй. Рассмотрим, как будет происходить физический процесс (см. рис. 1). Пуля летит, попадает в шар, происходит неупругий удар. Теперь приходит в движение система «шар + пуля», траектория движения которой представляет собой дугу окружности.
3. Зададимся вопросом, какие физические законы следует применить для решения задачи. Чтобы понять, с какой скоростью начнёт двигаться система «шар + пуля» сразу после столкновения, применим закон сохранения импульса для неупругого удара:
.
Направим ось OX горизонтально вправо и спроецируем скорости:
.
Выразим скорость системы «шар + пуля»:
.
4. В результате столкновения пули с шаром система приобретает кинетическую энергию, которая в наивысшей точке движения перейдёт полностью в потенциальную. На рисунке отмечен нулевой уровень потенциальной энергии. Тогда в наивысшей точке система «шар + пуля» будет иметь потенциальную энергию
.
Воспользуемся законом сохранения энергии для системы «шар + пуля»:
.
Подставим формулу в выражение выше и выразим оттуда :
;
5. Найдём численное значение:
.
Ответ: .
Пример 2
Разберём качественную задачу, решение которой будет полезно при решении задач на законы сохранения. Два шара массами , двигаются навстречу друг другу со скоростями , в горизонтальном направлении. Определить скорости шаров в результате центрального абсолютно упругого удара.
Решение
 Рис. 2. Иллюстрация к примеру
Рис. 2. Иллюстрация к примеру
1. Первым делом разберёмся с терминологией. Абсолютно упругий удар — это такой удар, в результате которого механическая энергия тел не переходит в другие виды энергии, то есть энергия сохраняется. А центральный удар — это удар, при котором тела двигаются вдоль линии, соединяющей центры масс этих тел. Рассмотрим случай, в котором шары после удара разлетелись в противоположные стороны.
2. Будем предполагать, что шары образуют замкнутую систему. Тогда для центрального абсолютно упругого удара выполняются закон сохранения импульса (ЗСИ) и закон сохранения энергии (ЗСЭ).
Начнём с ЗСИ:
.
Спроецируем скорости на ось ОХ:
.
Запишем ЗСЭ:
.
3. Наша задача — решить систему уравнений относительно величин и .
.
Преобразуем систему:
,
.
Поделим второе уравнение системы на первое:
.
Теперь рассмотрим новую систему, которая легко решается:
.
4. После небольших преобразований получаем выражения для скоростей:
.
5. Из анализов конечного результата можно заметить, что если массы шаров одинаковы, то тела просто обмениваются скоростями:
;
.
 Рис. 3. Иллюстрация к примеру
Рис. 3. Иллюстрация к примеру
6. Возможна ситуация, когда шары после удара двигаются в одном направлении.
Решение такой задачи аналогично предыдущей, но с учётом новых проекций скоростей.
При абсолютно неупругом ударе закон сохранения импульса выполняется, а закон сохранения энергии — нет. Энергия может выделиться в виде теплоты или пойти на изменение внутренней энергии тел.
В случае абсолютно упругого удара выполняется как закон сохранения импульса, так и закон сохранения энергии.
Пример 3
На столе лежит невесомая пружина жёсткостью 1 кН/м, прикреплённая одним концом к грузу массой 0,2 кг, а другим к стене. Груз сдвигают, сжимая пружину, и отпускают. Найдите длину, на которую сжали пружину, если после отпускания груза его скорость достигла величины 3 м/с. Трением пренебречь.
Решение
1. Перечислим исходные данные:
.
 Рис. 4. Иллюстрация к примеру
Рис. 4. Иллюстрация к примеру
2. Как только мы сожмём пружину, так сразу же в ней возникнет сила упругости, которая захочет вернуть пружину в исходное положение. По условию трением следует пренебречь, тогда система начнёт совершать гармонические колебания, во время которых энергия будет переходить из потенциальной в кинетическую. Момент, когда пружина сжата, изображён на рисунке 4.
 Рис. 5. Иллюстрация к примеру
Рис. 5. Иллюстрация к примеру
Как только мы отпустим груз, так сразу пружина придёт в движение, и проходя положение равновесия, груз достигнет максимальной скорости (рис. 5).
3. Сила тяжести и сила реакции опоры направлены перпендикулярно направлению движения. Рассмотрим замкнутую систему «груз + пружина», для которой в отсутствие сил трения будет выполняться закон сохранения энергия:
.
Выразим отсюда :
.
Ответ: .
Упражнение 1
1. Груз массой 0,4 кг падает с некоторой высоты на подложку массой 2 кг, закреплённую на пружине. Определите наибольшее сжатие пружины, если в момент удара скорость груза равнялась 8 м/с. Жёсткость пружины = 1 кН/м.
2. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жёстком стержне, и застревает в нём. Масса пули в 800 раз меньше массы шара. Расстояние от точки подвеса стержня до центра 2 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 7°.
Контрольные вопросы
1. Как выглядит закон сохранения импульса при неупругом ударе?
2. Что такое центральный удар?
3. Что называют полной механической энергией?
Упражнение 1
1. ≈ 9,3 см
2. ≈ 437 м/с

