Все уроки по всем предметам школьной программы ФГОС

Вписанная окружность

План урока

Определить понятие вписанной окружности;
Доказать теорему о вписанной в треугольник окружности;
Определить понятие окружности, вписанной в четырехугольник;
Доказать свойство и признак описанного четырехугольника;
Доказать формулу площади описанного многоугольника;
Рассмотреть применение свойства и признака описанного четырехугольника, формулы площади описанного многоугольника.

Цели урока

Знать определение вписанной окружности, описанного многоугольника, теорему об окружности, вписанной в треугольник, свойство и признак описанного четырехугольника, формулу площади описанного многоугольника;
Уметь применять свойство и признак описанного четырехугольника, формулу площади описанного многоугольника.

Разминка

Чем является геометрическое место точек, равноудаленных от сторон угла;
Формулы для нахождения площади треугольника;
Свойства касательной к окружности, отрезков касательных к окружности.

Вписанная в треугольник окружность

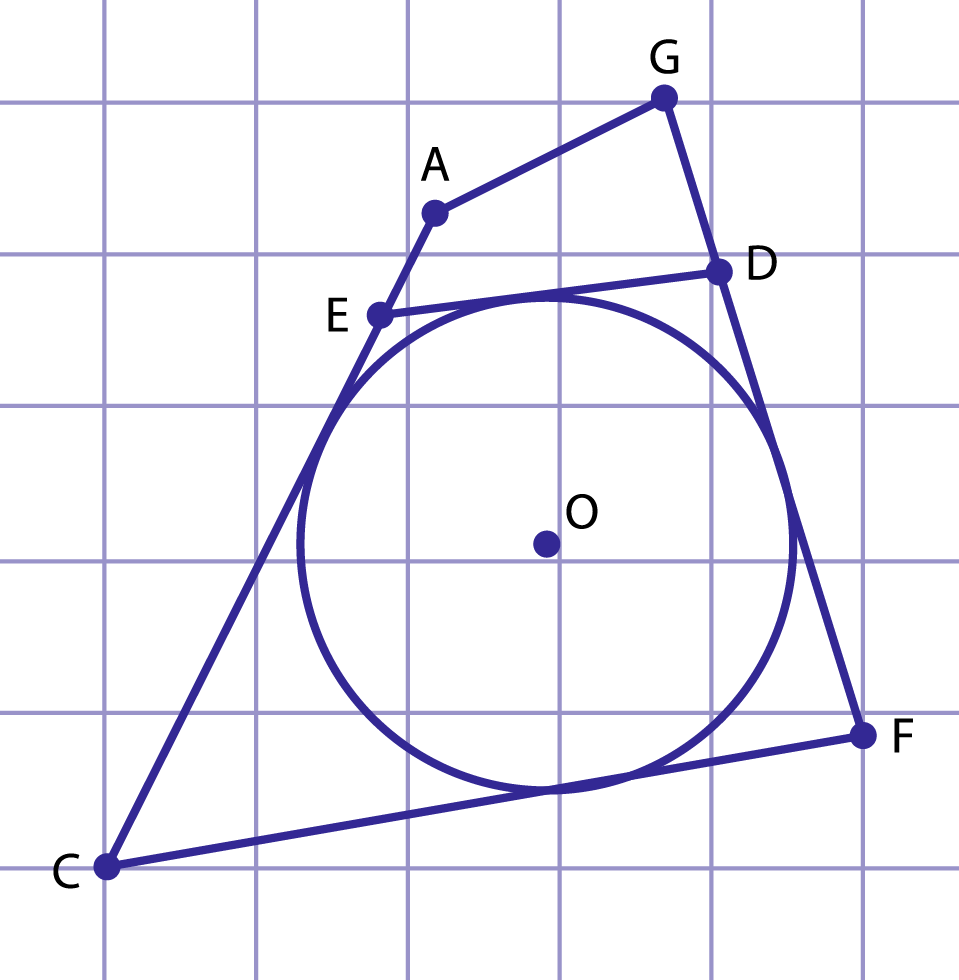Рис. 1. Описанный четырехугольник CEDF

Окружность называется вписанной в многоугольник, если она касается всех его сторон (т.е. прямые, содержащие стороны многоугольника, касаются окружности в точках, лежащих на сторонах). При этом многоугольник называется описанным около окружности.

На рис. 1 четырехугольник $C E D F$ описан около окружности с центром $O$ , а четырехугольник $C A G F$ не является описанным около этой окружности, так как сторона $A G$ не касается окружности. На рис. 2 треугольник $A B C$ описан около окружности с центром $O$ .

Докажем теорему об окружности, вписанной в этот треугольник.

Теорема

В любой треугольник можно вписать окружность, и притом единственную.

Доказательство

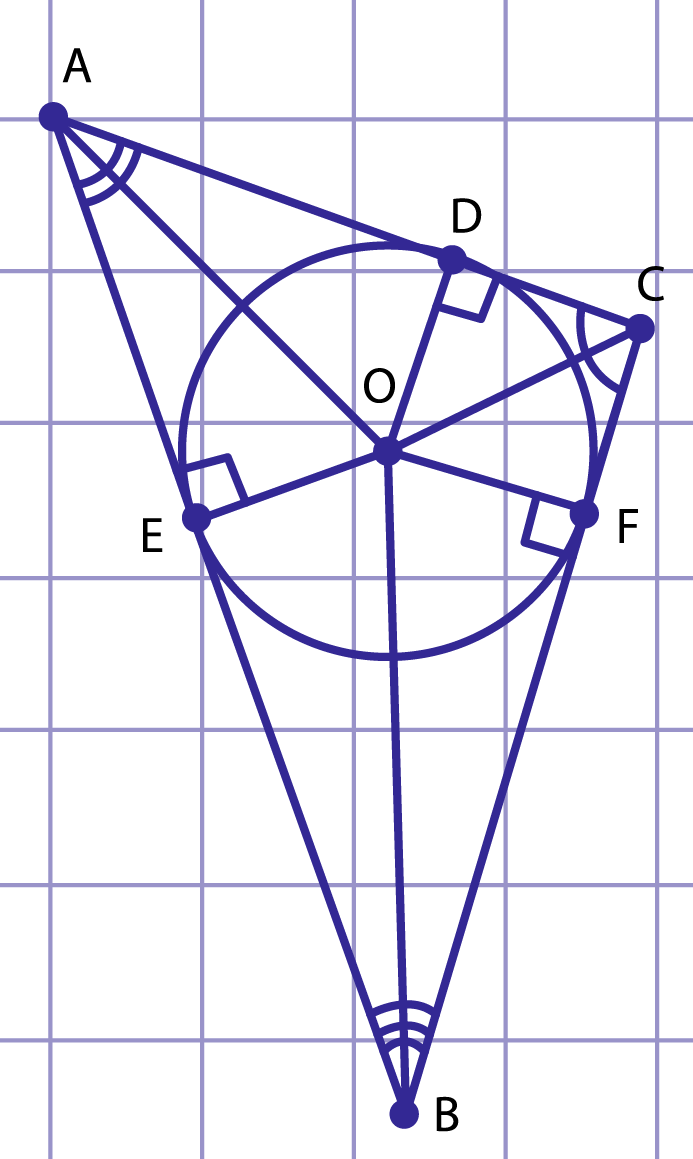Рис. 2. Окружность, вписанная в треугольник ABC

Рассмотрим треугольник $A B C$ . Пусть его биссектрисы пересекаются в точке $O$ (рис. 2). Тогда по теореме о биссектрисе угла точка $O$ равноудалена от сторон треугольника. Таким образом, три перпендикуляра, проведенные из точки $O$ к сторонам данного треугольника, равны, $O D = O E = O F$ . Следовательно, существует окружность с центром $O$ , которая касается всех сторон треугольника $A B C$ в точках $D$ , $E$ , $F$ , так как они перпендикулярны к радиусам $O D$ , $O E$ , $O F$ .

Докажем методом от противного, что эта окружность единственная.

Допустим, что в треугольник можно вписать еще одну окружность, отличную от построенной. Тогда ее центр одинаково удален от сторон треугольника и совпадает с $O$ — точкой пересечения биссектрис треугольника. Радиус этой окружности равен расстоянию от точки $O$ до сторон треугольника. Таким образом, эта окружность совпадает с построенной.

Теорема доказана.

Пример 1

В треугольник $A B C$ со сторонами $A B = 5 м$ , $B C = 7 м$ , $A C = 10 м$ вписана окружность. Прямая, пересекающая стороны $A B$ и $B C$ в точках $M$ и $K$ , касается этой окружности. Найдите периметр треугольника $M B K$ .

Решение

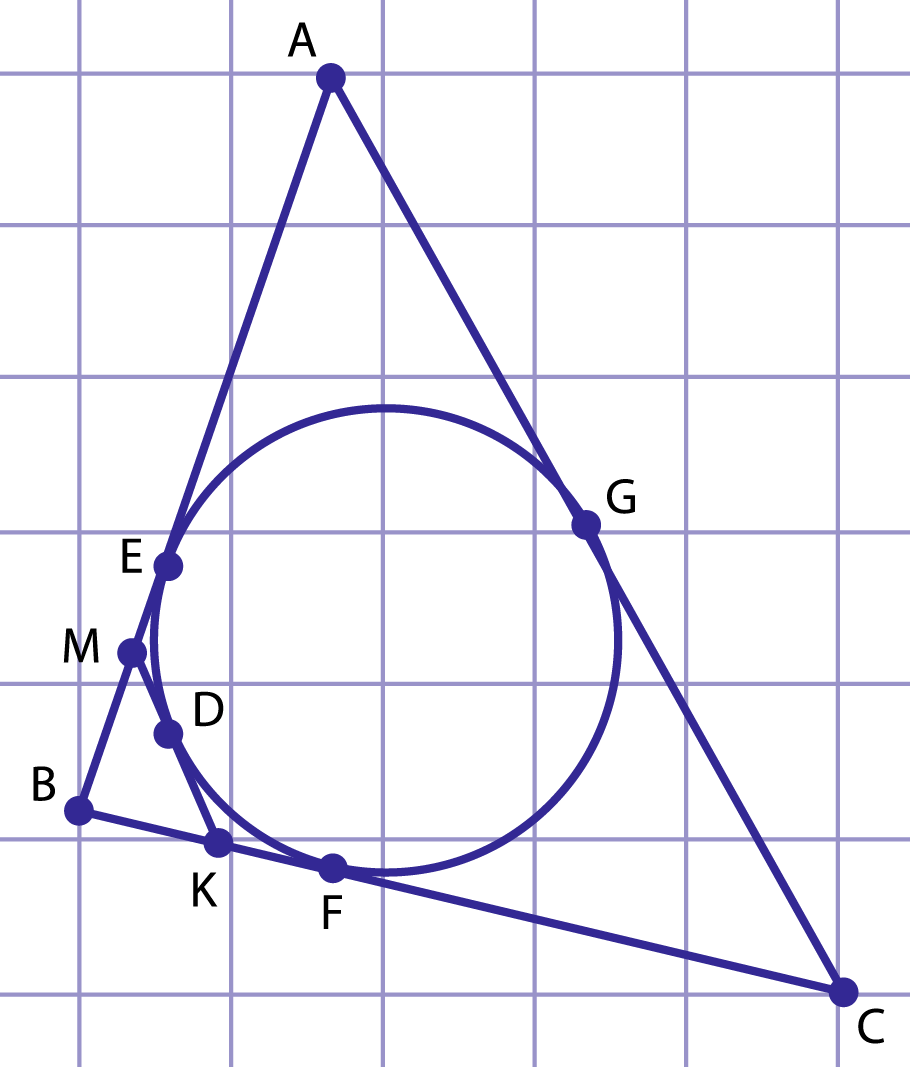Рис. 3. К решению примера 1

Пусть стороны $A B$ , $B C$ и $A C$ касаются окружности в точках $E$ , $F$ и $G$ соответственно, отрезок $M K$ касается окружности в точке $D$ . Тогда, по свойству отрезков касательных, $(B E = B F, A E = A G, C F = C G)$ ,

$A E + C F = A G + G C = A C = 10 м$ ,

$M K = M D + D K = M E + K F$ .

Периметр треугольника $M B K$ :

$P_{M B K} = B M + B K + M K = B M + B K + M E +$

$+ K F = B E + B F = A B + B C - A C =$

$= 5 + 7 - 10 = 2 (м)$

Ответ: $2 м$ .

Вписанная в четырехугольник окружность

Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности.

Четырехугольник $A B C D$ на рис. 4 является описанным около окружности. Иначе говорят, что окружность вписана в четырехугольник. Оказывается, не в любой четырехугольник можно вписать окружность. Докажем соответствующие свойство и признак.

Теорема (свойство описанного четырехугольника)

В описанном четырехугольнике суммы противоположных сторон равны.

Доказательство

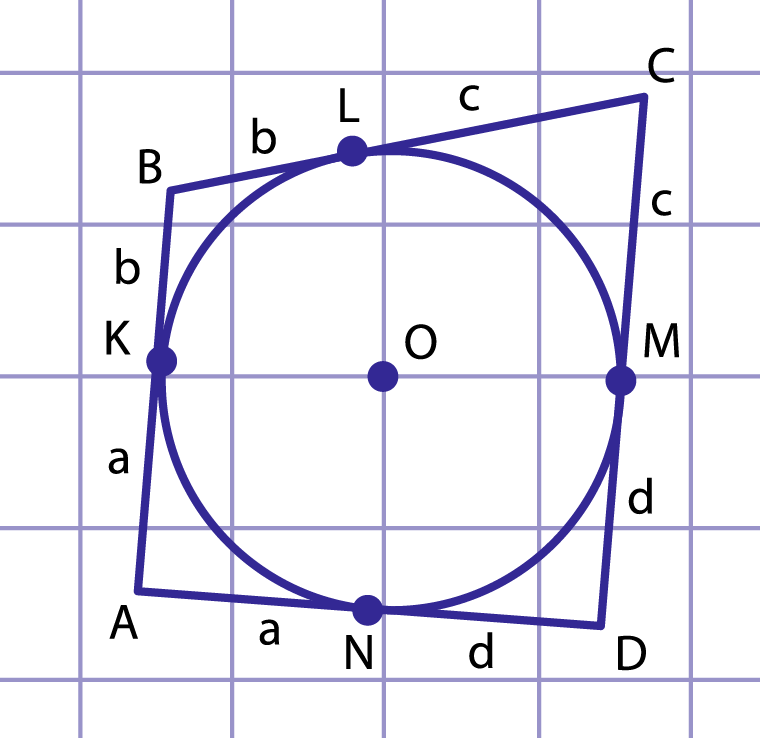Рис. 4. Четырехугольник ABCD описан около окружности

Пусть стороны четырехугольника $A B C D$ касаются вписанной окружности в точках $K$ , $L$ , $M$ и $N$ (рис. 4).

По свойству отрезков касательных $A K = A N$ , $B K = B L$ , $C L = C M$ , $D M = D N$ .

С учетом обозначений на рис. 4

$A B + C D = a + b + c + d = A D + B C$ .

Теорема доказана.

Теорема (признак описанного четырехугольника)

Если в четырехугольнике суммы противоположных сторон равны, то в него можно вписать окружность.

Доказательство

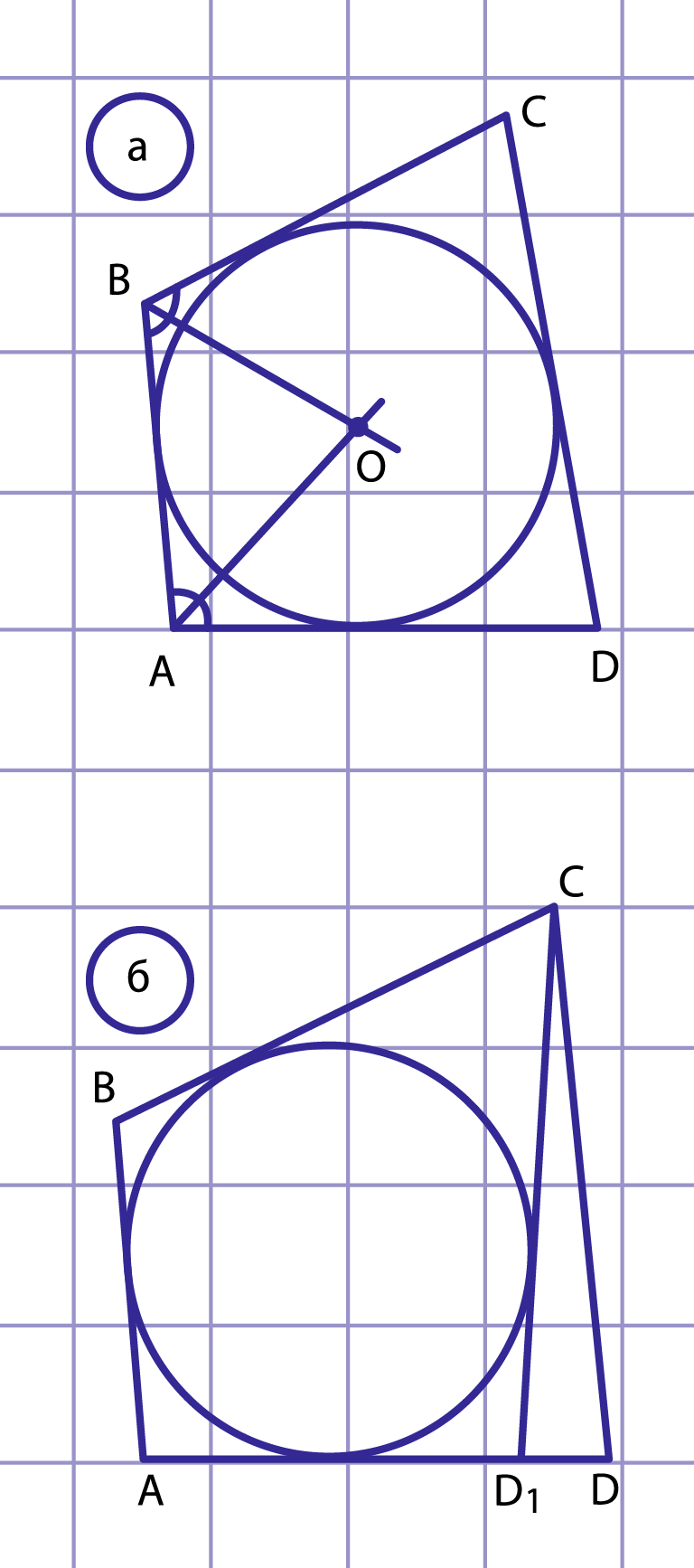Рис. 5. К доказательству признака описанного четырехугольника

Пусть в четырехугольнике $A B C D$ с наименьшей стороной $A B$ $A B + C D = A D + B C$ . Поскольку по теореме о биссектрисе угла точка $O$ (точка пересечения биссектрис углов $A$ и $B$ ) равноудалена от сторон $A B$ , $B C$ и $A D$ , то можно построить окружность с центром $O$ , которая касается этих трех сторон (рис. 5, а). Докажем от противного, что эта окружность касается также стороны $C D$ .

Предположим, что это не так. Тогда прямая $C D$ либо не имеет общих точек с окружностью, либо является секущей окружности. Рассмотрим первый случай (рис. 5, б). Проведем через точку $C$ касательную к окружности, которая пересекает сторону $A D$ в точке $D_{1}$ . Тогда по свойству описанного четырехугольника $A B C D_{1}$ $B C + A D_{1} = A B + C D_{1}$ . Но по условию $A D + B C = A B + C D$ . Вычитая из второго равенства первое, имеем:

$A D - A D_{1} = C D - C D_{1}$ , т. е. $D D_{1} = C D - C D_{1}$ , что противоречит неравенству треугольника для треугольника $C D_{1} D$ . Таким образом, наше предположение неверно. Аналогично можно доказать, что прямая $C D$ не может быть секущей окружности. Итак, окружность касается стороны $C D$ , т.е. четырехугольник $A B C D$ описанный.

Теорема доказана.

Замечание. Напомним, что в данных теоремах рассматриваются только выпуклые четырехугольники.

Следствие

В любой ромб можно вписать окружность.

Если в параллелограмм вписана окружность, то он является ромбом.

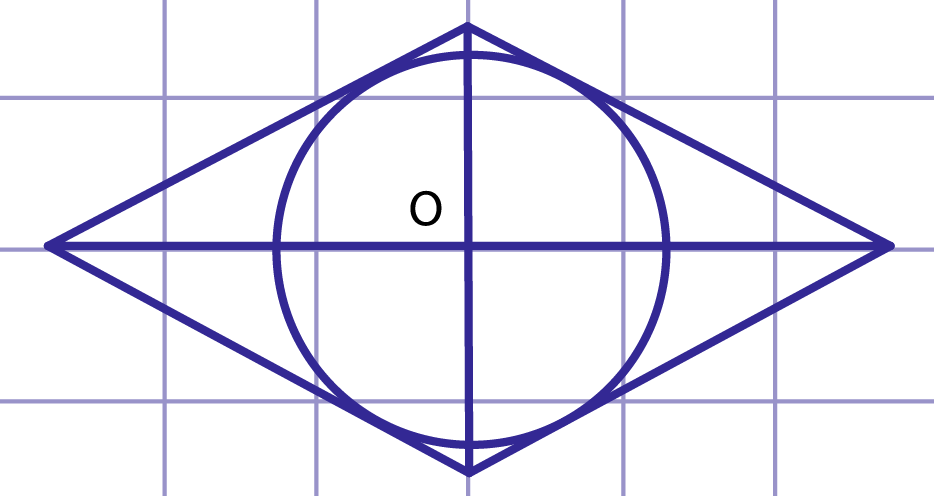Рис. 6. Ромб, описанный около окружности

Ромб, описанный около окружности, изображен на рисунке 6. Центр вписанной окружности является точкой пересечения диагоналей ромба.

Действительно, диагонали ромба являются биссектрисами углов ромба, следовательно, точка пересечения диагоналей равноудалена от сторон ромба.

Формула площади описанного многоугольника

Теорема

Если в многоугольник вписана окружность, то площадь многоугольника равна произведению его полупериметра на радиус этой окружности:

$S = p r$ ,

где $p$ – полупериметр многоугольника, $r$ – радиус вписанной окружности.

Доказательство

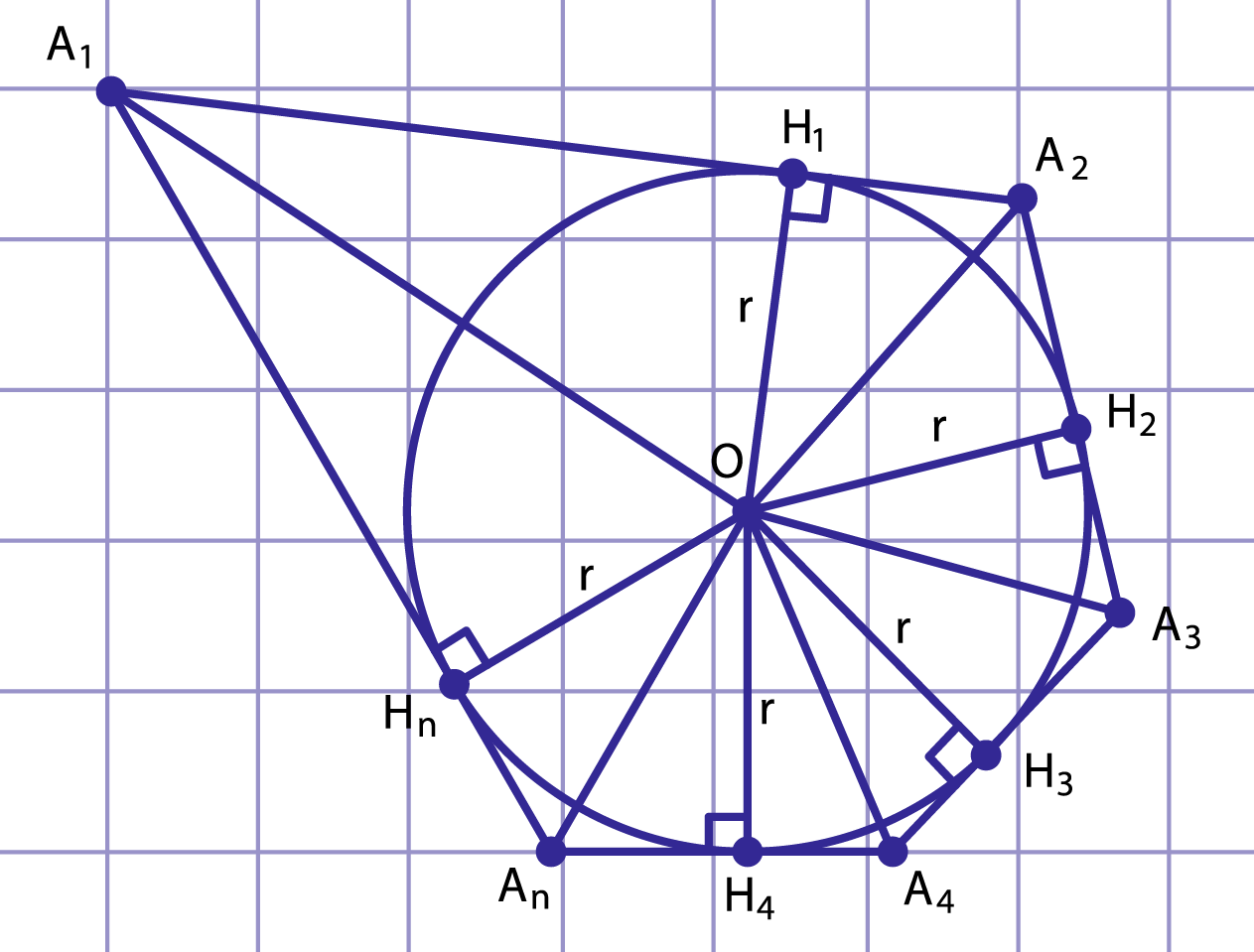Рис. 7. К доказательству теоремы о площади описанного многоугольника

Рассмотрим многоугольник $A_{1} A_{2} A_{3} \dots A_{n}$ , в который вписана окружность с центром $O$ и радиусом $r$ (рис. 7).

Соединим центр окружности с вершинами многоугольника, разделив многоугольник на $n$ треугольников. В треугольнике $A_{1} O A_{2}$ высота $O H_{1}$ равна радиусу окружности, поэтому $S_{A_{1} O A_{2}} = \frac{1}{2} A_{1} A_{2} \cdot r$ .

Площадь каждого из $n$ треугольников равна половине произведения стороны многоугольника на радиус окружности, тогда площадь многоугольника равна сумме площадей треугольников:

$S_{A_{1} A_{2} A_{3} \dots A_{n}} = S_{A_{1} O A_{2}} + S_{A_{2} O A_{3}} + \dots + S_{A_{n} O A_{1}} =$

$= \frac{1}{2} A_{1} A_{2} \cdot r + \frac{1}{2} A_{2} A_{3} \cdot r + \dots + \frac{1}{2} A_{1} A_{n} \cdot r =$

$= \frac{1}{2} r (A_{1} A_{2} + A_{2} A_{3} + \dots + A_{1} A_{n}) = \frac{1}{2} P_{A_{1} A_{2} A_{3} \dots A_{n}} \cdot r = p r$ .

Теорема доказана.

Пример 2

Основание равнобедренного треугольника равно 6 м, а высота, проведенная к нему, - 4 м. Найдите радиус окружности, вписанной в треугольник.

Решение

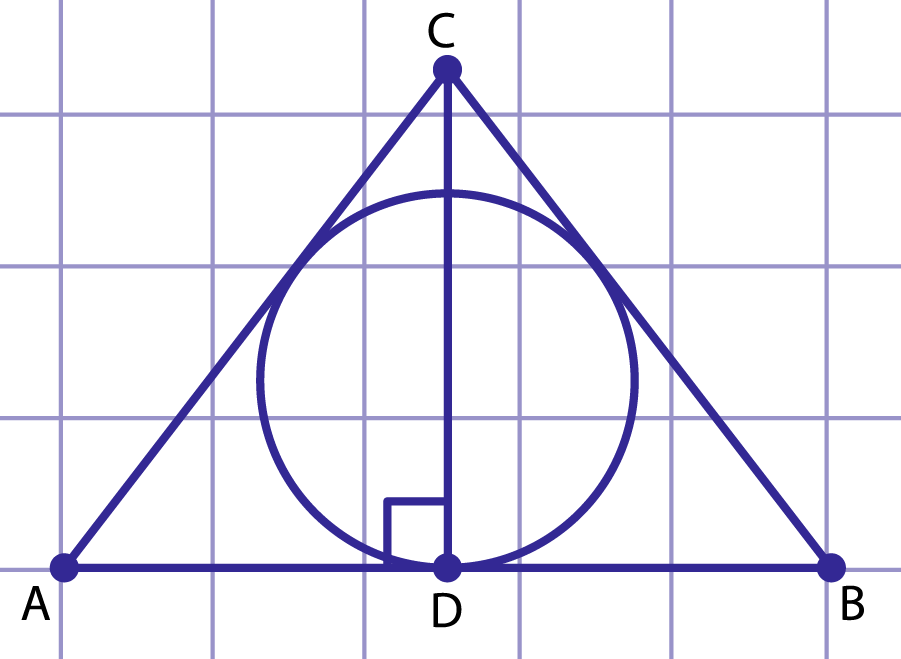Рис. 8. К решению примера 2

Рассмотрим равнобедренный треугольник $A B C$ , $A B = 6 м$ , высота $C D$ равна $4 м$ (рис. 8). Пусть $r$ – радиус окружности, вписанной в $A B C$ .

По свойству равнобедренного треугольника $C D$ – медиана, $A D = 3 м$ . По теореме Пифагора $A C = \sqrt{A D^{2} + C D^{2}} = 5 м$ .

Применим метод площадей.

$S_{A B C} = \frac{1}{2} A B \cdot C D$ , $S_{A B C} = \frac{A B + B C + A C}{2} \cdot r$ .

$\frac{1}{2} \cdot 6 \cdot 4 = \frac{6 + 5 + 5}{2} \cdot r$ ,

$r = \frac{12}{8} = 1, 5 м$ .

Ответ: 1,5 м.

Упражнения

1. В треугольнике $A B C$ биссектрисы углов $A$ и $C$ пересекаются в точке $O$ . Найдите угол $B A C$ , если $A B = B C$ , $∠ A B O = 35 °$ .

2. Найдите периметр:

а) описанного четырехугольника, три последовательные стороны которого равны 7 см, 9 см и 8 см;

б) описанной трапеции, боковые стороны которой равны 3 см и 11 см.

3. Равнобедренная трапеция описана около окружности. Найдите:

а) боковую сторону трапеции, если ее средняя линия равна 7 см;

б) среднюю линию трапеции, если ее периметр равен 16 см.

4. Найдите среднюю линию прямоугольной трапеции, в которой большая боковая сторона равна 10 см, а радиус вписанной окружности равен 3 см.

Контрольные вопросы

1. Даны треугольник и окружность. Определите, является ли данная окружность вписанной в треугольник, если:

а) центр окружности равноудален от всех сторон треугольника;

б) центр окружности равноудален от всех вершин треугольника;

в) все стороны треугольника — хорды окружности;

г) все стороны треугольника касаются окружности.

2. Точка $O$ — центр окружности, вписанной в треугольник $A B C$ . Означает ли это, что:

а) $A O = O B$ ;

б) $∠ A B O = ∠ C B O$ ;

в) точка $O$ может лежать вне данного треугольника?

3. В какой прямоугольник можно вписать окружность? Около какого ромба можно описать окружность?

4. Трапеция $A B C D$ ( $A B ∥ B C$ ) описана около окружности. Как построить точку $M$ такую, чтобы треугольник $A M D$ был описан около той же окружности?

Ответы на упражнения

1. 55°.

2 а) 30 см; б) 28 см.

3 а) 7 см; б) 4 см.

4 8 см.

Конспект урока: Вписанная окружность

Окружность

Вписанная в треугольник окружность

Вписанная в четырехугольник окружность

Формула площади описанного многоугольника