- Взаимное расположение прямой и окружности;
- Касательная к окружности.
- Знать взаимное расположение окружности и прямой, определение касательной к окружности, свойства и признак касательной к окружности;
- Уметь применять свойства и признак касательной.
- Определение окружности;
- Свойства равнобедренного треугольника;
- Теорема Пифагора.
Взаимное расположение прямой и окружности
Количество общих точек прямой и окружности определяет их взаимное расположение. Если прямая проходит через центр окружности, то она пересекает окружность в двух точках – концах диаметра, лежащего на данной прямой.
Рассмотрим прямую , которая не проходит через центр окружности радиуса . Проведем перпендикуляр к прямой и обозначим буквой его длину, т.е. проведем расстояние от центра окружности до прямой.
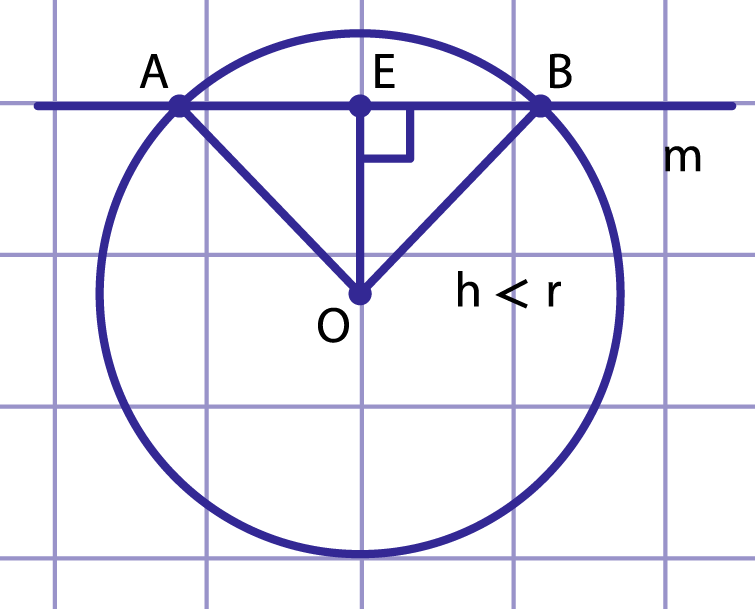 Рис. 1. Расстояние от центра до прямой меньше радиуса
Рис. 1. Расстояние от центра до прямой меньше радиуса
Рассмотрим взаимное расположение прямой и окружности в зависимости от соотношения и . Возможны три случая:
1) . На прямой отложим отрезки и по разные стороны от точки длиной (рис. 1). По теореме Пифагора
,
.
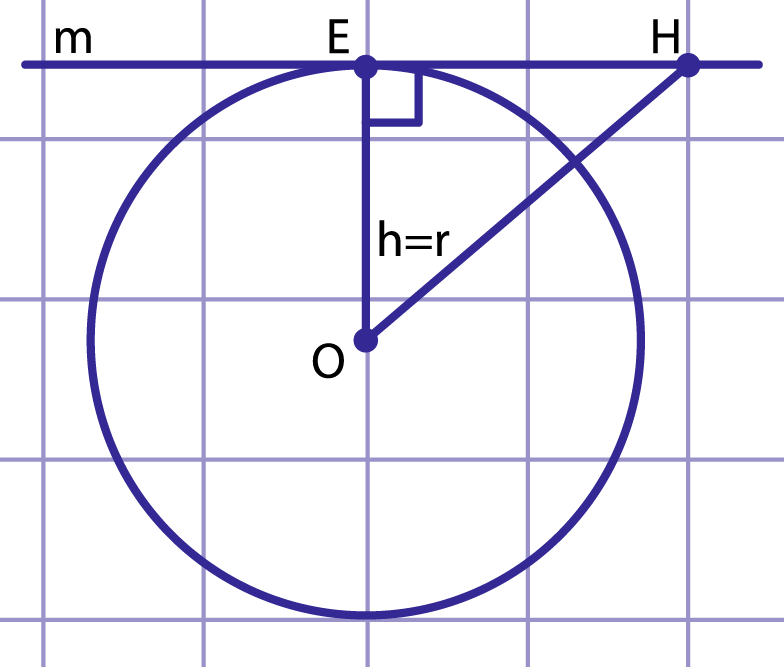 Рис. 2. Расстояние от центра до прямой равно радиусу
Рис. 2. Расстояние от центра до прямой равно радиусу
Точки и лежат на окружности, т.е. являются общими точками для прямой и окружности.
Докажем, что других общих точек прямая и окружность с центром в точке и радиусом не имеют. Допустим, что они имеют еще одну общую точку . Тогда , треугольник равнобедренный. Медиана треугольника , проведенная к основанию , является высотой этого треугольника, следовательно и , точки и не совпадают, т.к. не совпадают точки и . Тогда из точки к прямой проведено более одного перпендикуляра, что невозможно.
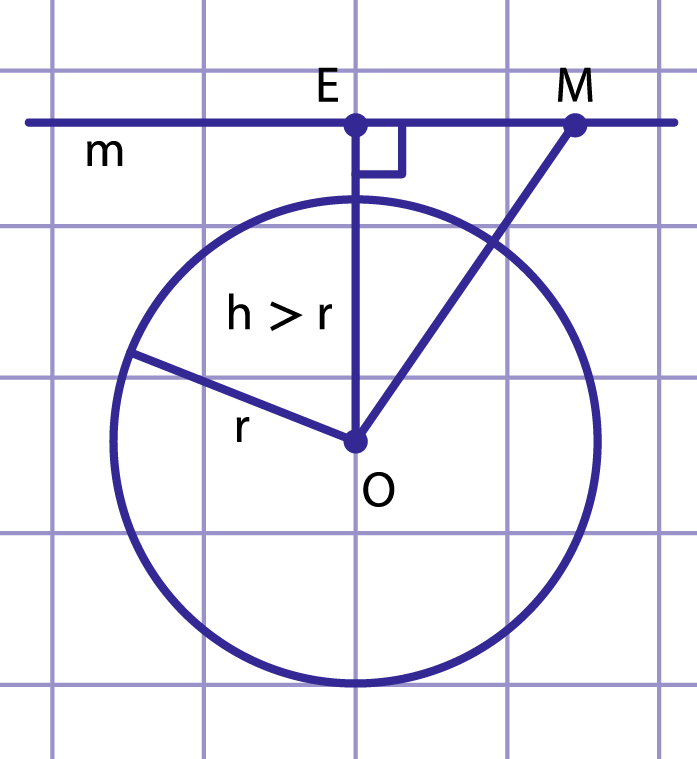 Рис. 3. Расстояние от центра до прямой больше радиуса
Рис. 3. Расстояние от центра до прямой больше радиуса
2) . Тогда , следовательно точка лежит на окружности, значит является общей точкой прямой и окружности (рис. 2). Прямая и окружность не имеют других общих точек, поскольку для любой точки прямой , отличной от точки , (наклонная больше перпендикуляра ), точка не лежит на окружности.
3) . В этом случае , поэтому для любой точки прямой .
(рис. 3). Следовательно, точка не лежит на окружности.
Если расстояние от центра окружности до прямой меньше радиуса окружности (), то прямая и окружность имеют две общие точки. Такая прямая называется секущей по отношению к окружности.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Пример 1
Меньшая боковая сторона прямоугольной трапеции делится точкой в отношении 2:3. Определите взаимное расположение прямых, содержащих стороны трапеции, и окружности с центром в точке и радиуса 6 см, если , , .
Решение
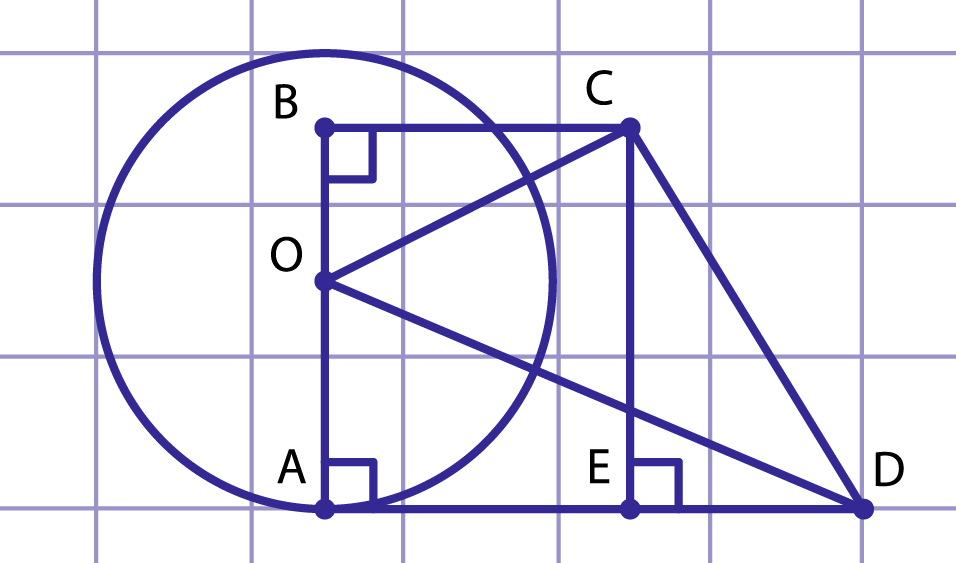 Рис. 4. К решению примера 1
Рис. 4. К решению примера 1
Поскольку боковая сторона наименьшая, то углы и прямые (рис. 4). Отрезок делится точкой в отношении 2:3, следовательно
, .
Расстояние от центра окружности до прямой меньше радиуса, значит секущая.
Расстояние от центра окружности до прямой равно радиусу, значит – касательная. Прямая проходит через центр окружности, – секущая.
Вычислим расстояние от точки до прямой , используя метод площадей.
,
,
,
.
– высота трапеции, по теореме Пифагора в прямоугольном треугольнике гипотенуза . , где - высота треугольника , проведенная к стороне . Тогда , что больше 6 см. Следовательно прямая не пересекает окружность.
Ответ: и секущие, касательная, не пересекает окружность.
Касательная к окружности
Рассмотрим теперь прямую, имеющую с окружностью только одну общую точку.
Определение
Касательной к окружности называется прямая, имеющая с окружностью единственную общую точку.
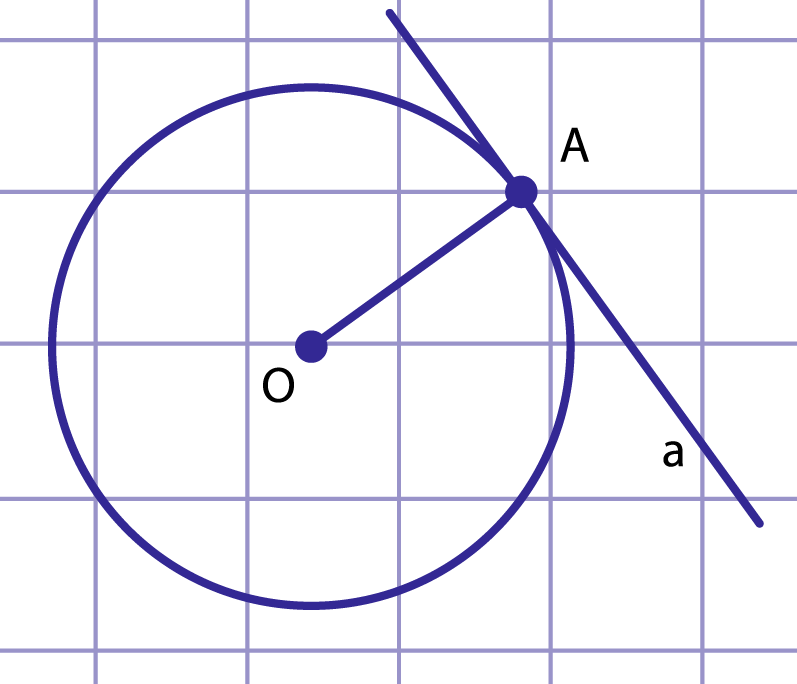 Рис. 5. Касательная к окружности
Рис. 5. Касательная к окружности
Общая точка касательной и окружности называется точкой касания. На рис. 5 прямая является касательной к окружности с центром . Иначе говоря, прямая касается окружности с центром в точке .
Определим взаимное расположение касательной и радиуса окружности, проведенного в точку касания.
Теорема ( свойство касательной к окружности )
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство
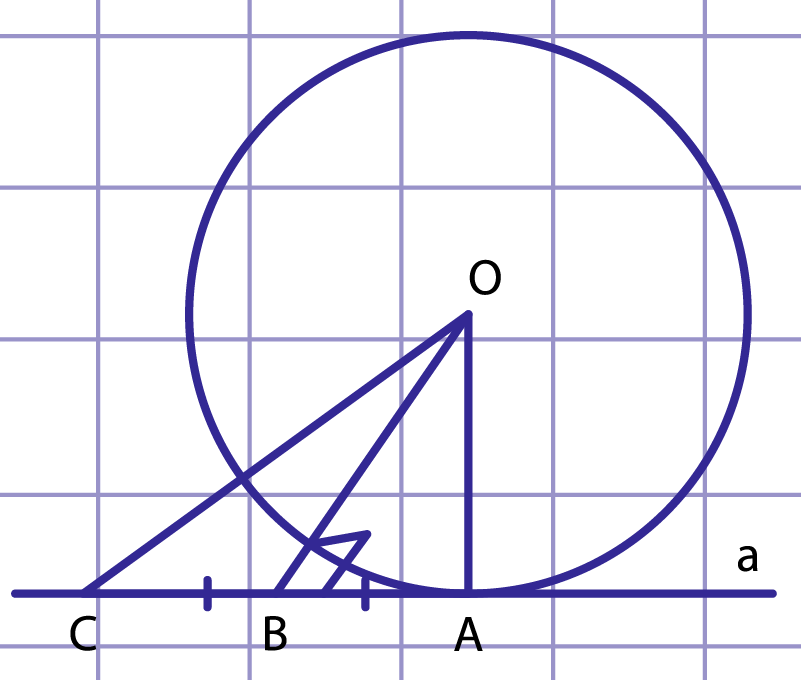 Рис. 6. К доказательству свойства касательной к окружности
Рис. 6. К доказательству свойства касательной к окружности
Пусть прямая касается окружности с центром в точке (рис. 6). Докажем, что . Применим метод доказательства от противного.
Пусть отрезок не является перпендикуляром к прямой . Тогда по теореме о существовании и единственности перпендикуляра к прямой из точки можно провести перпендикуляр к прямой .
На луче от точки отложим отрезок , равный , и соединим точки и . Поскольку по построению отрезок — медиана и высота треугольника , то этот треугольник равнобедренный с основанием , то есть . Таким образом, расстояние между точками и равно радиусу окружности, и, по определению радиуса, точка должна лежать на данной окружности. Но это противоречит определению касательной, поскольку — единственная общая точка окружности с прямой . Из этого противоречия следует, что наше предположение неверно, то есть .
Теорема доказана.
Пусть из точки к окружности проведены две касательные, и – точки касания. Отрезки и называются отрезками касательных , проведенными из точки (рис. 7). Они обладают следующим свойством:
Теорема ( свойство отрезков касательных )
Отрезки касательных к окружности, проведенные из данной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство
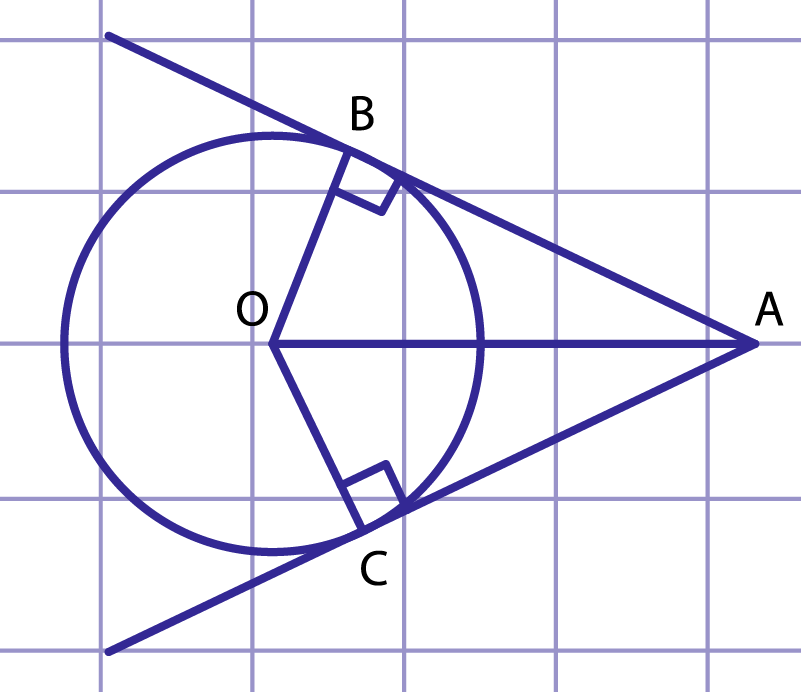 Рис. 7. Отрезки касательных, проведенных к окружности из точки A
Рис. 7. Отрезки касательных, проведенных к окружности из точки A
Пусть и – отрезки касательных, проведенных к окружности с центром из точки (рис. 7). Рассмотрим треугольники и . По свойству касательной к окружности , , то есть эти треугольники являются прямоугольными с общей гипотенузой и равными катетами
( как радиусы окружности). Следовательно, по гипотенузе и катету, откуда , .
Теорема доказана.
Докажем теорему, обратную теореме о свойстве касательной к окружности (признак касательной).
Теорема ( признак касательной )
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Доказательство
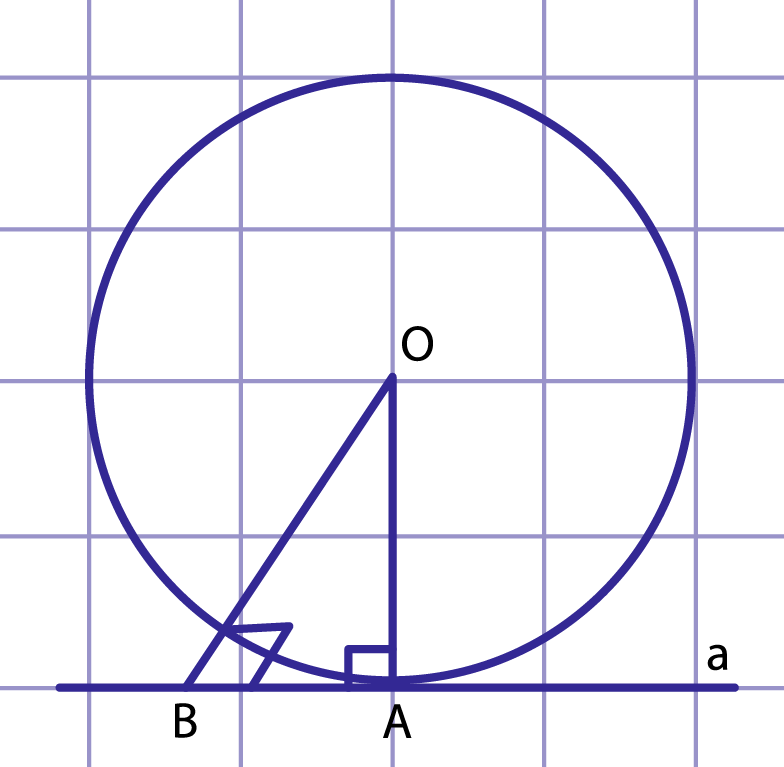 Рис. 8. К доказательству признака касательной
Рис. 8. К доказательству признака касательной
Пусть прямая проходит через точку , лежащую на окружности с центром , причем . Докажем, что — касательная к окружности. Согласно определению касательной нам необходимо доказать, что окружность имеет с прямой единственную общую точку. Снова применим метод доказательства от противного.
Пусть прямая имеет с окружностью общую точку , отличную от (рис. 8). Тогда из определения окружности как радиусы, то есть треугольник равнобедренный с основанием По свойству углов равнобедренного треугольника , что противоречит теореме о сумме углов треугольника.
Следовательно, точка — единственная общая точка окружности и прямой , значит, прямая — касательная к окружности.
Теорема доказана.
Пример 2
Через точку окружности радиуса проведены касательная и хорда, равная . Найдите угол между ними.
Решение
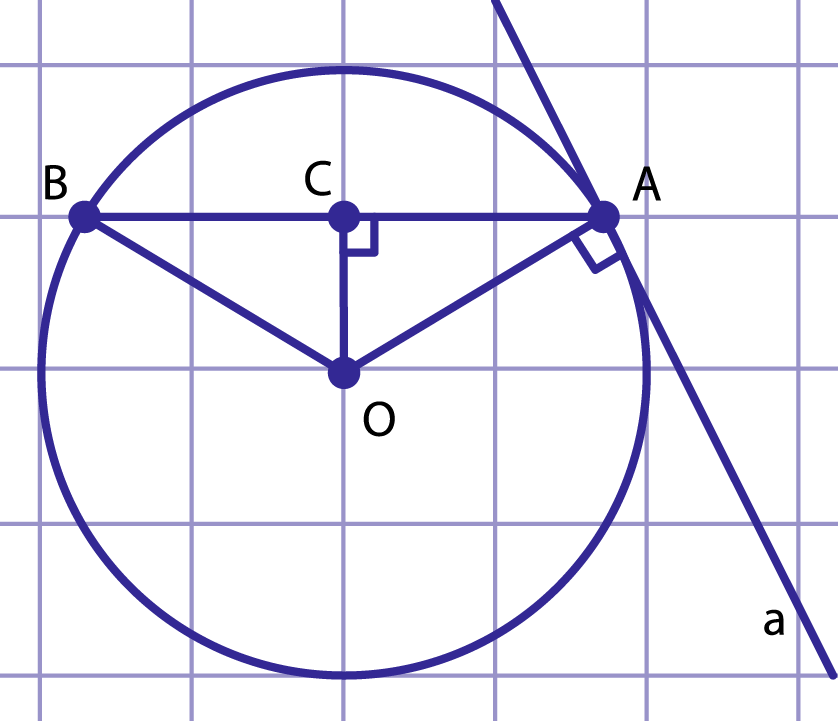 Рис. 9. К решению примера 2
Рис. 9. К решению примера 2
Рассмотрим окружность с центром в точке радиуса . Через точку окружности проведена касательная и хорда (рис. 9). Найдем угол между касательной и хордой .
Треугольник равнобедренный ( как радиусы), – высота и медиана данного треугольника, . В прямоугольном треугольнике , следовательно . По свойству касательной угол между радиусом и касательной равен , тогда угол между касательной и хордой равен .
Ответ: .
Упражнения
1. Прямая касается окружности с центром в точке . Найдите углы и , если .
2. Через точку окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.
3. Через концы хорды , равной радиусу окружности, проведены касательные, пересекающиеся в точке . Найдите угол .
Контрольные вопросы
1. Прямая касается окружности с центром в точке . Может ли треугольник иметь тупой угол?
2. Сколько касательных к данной окружности можно провести через точку, которая лежит:
а) на данной окружности;
б) внутри круга, ограниченного данной окружностью?
3. и — отрезки касательных, проведенных из точки к данной окружности. Определите вид треугольника .
1. и
2. 30°
3. 120°

