- Алфавитный подход к измерению информации
- Информационный вес символа произвольного алфавита
- Информационный объём сообщения
- Единицы измерения информации
- знать определения: информационный вес, бит, информационный объём
- знать способ нахождения информационного объёма сообщения
- уметь пояснять суть алфавитного подхода к измерению информации
- уметь находить информационный объём сообщения
- знать единицы измерения информации
- уметь переводить из одной единицы измерения в другую
Количество любой величины можно выразить, используя единицы измерения. Сопоставление измеряемой величины с единицей измерения помогает определить количество величины. Необходимо ответить на вопрос: сколько раз единица измерения укладывается в эту величину?
Нам известно, что существуют единицы измерения таких величин: например, масса может измеряться в граммах, время — в секундах, расстояние — в километрах и т. д.
А как ответить на вопрос: «Сколько за сегодняшний день человек получил информации?». Можно ответить «много» или «мало», но такой подход к измерению информации будет не совсем точным. Так как же измерить информацию?
Алфавитный подход к измерению информации. Информационный вес символа произвольного алфавита
Существует несколько подходов к измерению информации. Рассмотрим один из них.
Алфавитный подход позволяет измерять информационный объём сообщения на некотором языке (естественном или формальном), не связанный с содержанием этого сообщения.
При алфавитном подходе считается, что в сообщении каждый символ имеет свой вес — информационный вес, то есть несёт определённое количество информации.
Мощность алфавита влияет на информационный вес символа.
Информационный вес символа двоичного алфавита принят за минимальную единицу информации и называется 1 бит.
В прошлом параграфе мы выяснили, что разрядностью двоичного кода называют длину двоичной цепочки. Выделенная нами закономерность , где N — количество кодовых комбинаций, i — разрядность двоичного кода, говорит о том, что разрядность двоичного кода — это и есть информационный вес символа, который выражается в битах.
Данный подход к измерению количества информации используется для любого текста, несмотря на его содержательную часть. Бессмысленное сочетание символов также имеет информационный объём.
Информационный объём сообщения
Информационный объём сообщения представляет собой сумму информационных весов составляющих его символов.
Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i:
,
где К — количество символов в сообщении, а I — количество информации в сообщении, i — информационный вес символа.
Пример 1
Сообщение 10101001101 содержит 11 символов, значит, его информационный объём равен 11 битам.
Пример 2
Доклад, записанный буквами 32-символьного алфавита содержит 700 символов (включая пробелы). Найдите информационный объём доклада.
Решение:

Пример 3
Сообщение объёмом 930 битов состоит из 310 символов. Какова мощность алфавита, используемого для записи данного сообщения?
Решение
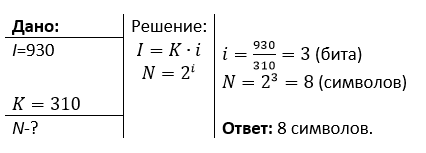
Единицы измерения информации
Для подготовки различных текстовых документов в настоящее время чаще всего используются компьютеры. Так называемый «компьютерный» алфавит состоит из 256 символов: в него включены прописные и строчные русские и латинские буквы, цифры, знаки препинания, знаки арифметических действий, скобки и т. д.
Имеет место выражение:
,
тогда несложно определить, чему равно i.
i = 8 битов.
Информационный вес каждого символа «компьютерного» алфавита равен 8 битам. Величина, равная 8 битам, будет называться байтом.
Несложно вычислить информационный объём текста, если информационный вес одного символа равен 1 байту.
Пример 4
В энциклопедии 3 тома, в каждом из которых порядка 80 страниц. На одной странице размещается в среднем 60 строк по 58 символов (включая пробелы) в каждой. Найдите информационный объём энциклопедии, если информационный вес одного символа равен 1 байту.
Решение

Очевидно, что бит и байт являются наименьшими единицами измерения информации. Для удобства вычислений используются более крупные единицы: килобайт, мегабайт, гигабайт, терабайт. Каждая следующая единица измерения больше предыдущей в 1 024 раза (рис. 1).
 Рис. 1. Единицы измерения информации
Рис. 1. Единицы измерения информации
Отметим, что существуют и другие, ещё больше единицы измерения
информации — после терабайта идут петабайт, эксабайт, зеттабайт, йотабайт, каждая из которых также больше предыдущей в 1 024 раза.
Пример 5
Возвращаясь к примеру 4, выразим информационный объём в Кб (килобайтах) и Мб (мегабайтах):
Решение:
835 200 ∶ 1 024 = 815,625 Кб,
815,625 ∶ 1 024 = 0,7965 Мб ≈ 0,8 Мб.
Ответ: 0,8 Мб.
Сравним разные объёмы информации:
1 байт — символ, введённый с клавиатуры;
100 Кб— доклад, состоящий из 5 листов;
1 Мб — рабочая тетрадь по информатике;
100 Мб — три школьных учебника;
1 Гб — прочитывает человек за всю жизнь;
3 Гб — фильм хорошего качества.
Контрольные вопросы
1. Объясните суть алфавитного подхода. Как определяется информационный объём сообщения при использовании данного подхода?
2. Что такое байт, килобайт, гигабайт, терабайт? Существуют ли ещё большие единицы измерения информации?
3. Информационный объём сообщения, подготовленного с помощью компьютера, равен 3,5 Кб. Сколько символов содержит данное сообщение?
4. Два сообщения содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 32 символа, второй — мощностью 64 символа. Во сколько раз различаются информационные объёмы сообщений?
Вопрос 3
K = 3 584 символов.
Вопрос 4
В 1,2 раза.

