- Обработка информации
- Типы обработки информации
- Граф
- Решение логических задач
- знать виды обработки информации
- знать определение графа
- уметь решать логические задачи
- уметь строить графы
- Что такое информационные процессы? Перечислите их.
- В чём заключается информационная деятельность человека?
- Приведите примеры процесса сбора информации.
- Что такое процесс обработки информации?
- Что такое входная и выходная информация?
Обработка информации. Типы обработки информации
Процесс обработки информации заключается в том, чтобы полученную — входную — информацию преобразовать и получить результат — выходную информацию.
Обработка информации бывает двух типов. Обработка первого типа заключается в том, что на выходе человек получает новое содержание, новую информацию благодаря исследованию объектов, логическим рассуждениям и обобщениям. Обработка второго типа — изменение формы представления характеризуется структурированием, кодированием и отбором информации.
Решение логических задач
Решение логических задач с помощь первого типа обработки информации (получение нового содержания) представляет собой использование таблиц, в которых объекты взаимосвязаны между собой. Связь между объектами можно отобразить цифрами 1 или 0 (знаками + или −). В таблице в каждой строке и каждой графе будет находиться только одна 1 (+), фиксирующая наличие связи между объектами. Это свойство можно использовать при решении логических задач.
Пример 1
На Всероссийской олимпиаде по информатике оказались пять мальчиков из Волгограда, Краснодара, Самары, Москвы и Тамбова: Ваня, Кирилл, Артём, Саша и Рома. На конференции их посадили за один стол. Волгоградец расположился между мальчиком из Тамбова и Ромой, краснодарец — между Ваней и Кириллом, а напротив оказались мальчик из Москвы и Артём. Саша не бывал в Краснодаре, а Ваня никогда не был в Волгограде и Тамбове, а мальчик из Тамбова с Кириллом уже встречались в прошлом году на олимпиаде по информатике. Кто из какого города приехал на Всероссийскую олимпиаду по информатике?
Решение
Анализ этого текста позволяет выделить два класса объектов: «мальчик» и «город». Нужно установить взаимно однозначное соответствие (выявить пары) между объектами этих классов. Наличие свойства у пары объектов «мальчик живёт в городе» будем обозначать 1 (или +), а его отсутствие — 0 (или −)
Отметим в таблице 1 свойства пар, следующие из условия задачи.
Таблица 1. Условие примера № 1
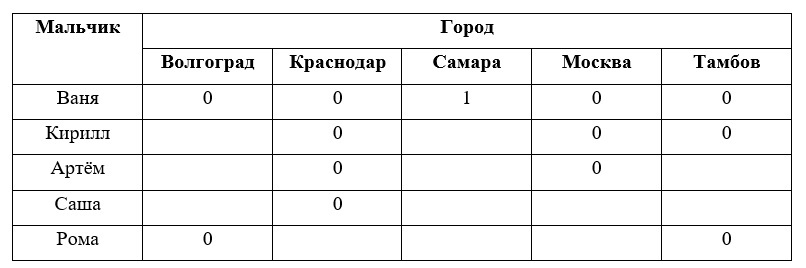
После этого остаётся проследить, чтобы в каждой строке и каждой графе обязательно была одна и только одна единица. Очевидно, что Рома из Краснодара, а значит, он не из Москвы, следовательно, Саша из Москвы. Так как Саша не из Тамбова, значит, из этого города приехал Артём. Остается, что Кирилл приехал из Волгограда (таблица 2).
Таблица 2. Анализ условия и логические рассуждения
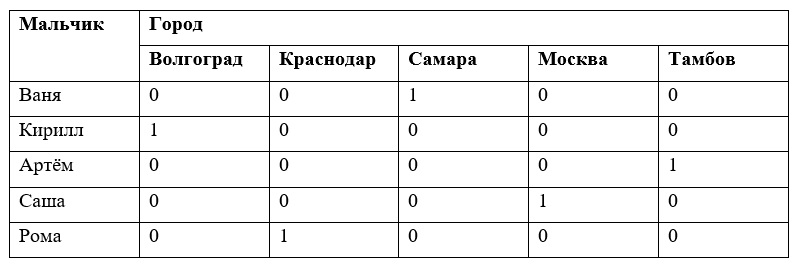
Ответ: Ваня приехал из Самары, Кирилл приехал из Волгограда, Артём приехал из Тамбова, Саша приехал из Москвы и Рома приехал из Краснодара.
Граф
Граф — это графическая схема, состоящая из структурированного материала, части которого взаимосвязаны.
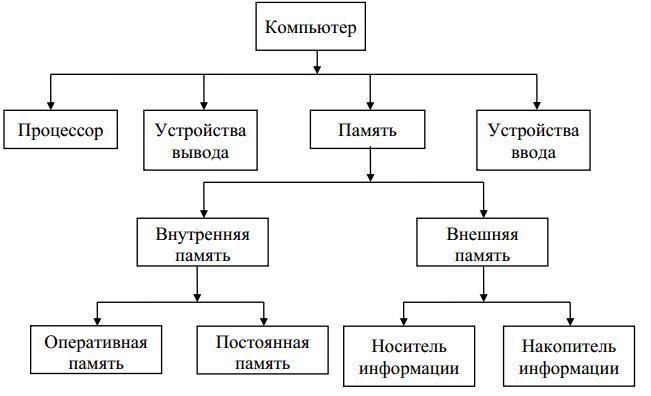 Рис. 1. Пример графа «Устройство компьютера»
Рис. 1. Пример графа «Устройство компьютера»
Граф состоит из вершин, связанных линиями. Вершины обозначаются точками, квадратами овалами и т. д. Линии, связывающие две соседние вершины, могут иметь направление (быть в виде стрелки) или не имеют направление. В первом случае линии называются дугами, во втором — рёбрами.
Примером графа является схема устройства компьютера (рис. 1).
Пример 2
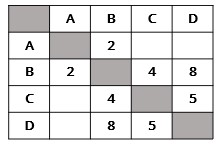 Рис. 2. Условие примера № 2
Рис. 2. Условие примера № 2
В таблице приведены расстояния между четырьмя посёлками. Если пересечение строки и столбца пусто, то между посёлками дороги нет. Изобразите схематически приведённую дорожную систему. С помощью графа определите кратчайший путь из посёлка А в D (рис. 2).
Решение
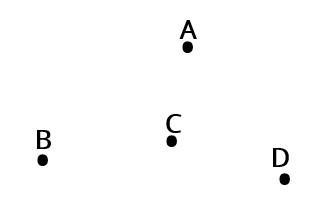 Рис. 3. Граф
Рис. 3. Граф
Поставим произвольно точки по количеству вершин: A, B, C, D (рис. 3).
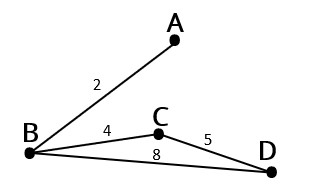 Рис. 4. Построение графа
Рис. 4. Построение графа
Соединим указанные точки линиями и подпишем числовые значения. Желательно, чтобы линии (рёбра) в графе не пересекались (рис. 4).
Из А в D существуют два пути:
A — B — C — D = 2 + 4 + 5 = 11,
A — B — D = 2 + 8 = 10 — кратчайший путь из А в D.
Ответ: 10.
Пример 3
Сколько существует трёхзначных чисел, составленных из цифр 5, 6, 7, при условии, что каждая цифра используется только один раз?
Решение
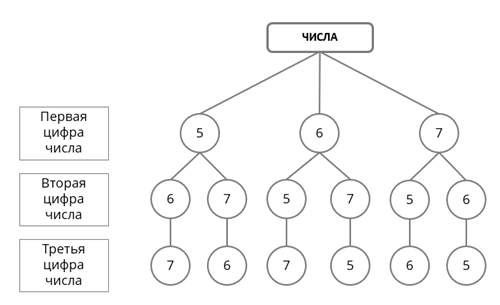 Рис. 5. Граф, составленный по условию задачи
Рис. 5. Граф, составленный по условию задачи
Для решения задачи составим граф (рис. 5).
Получим следующие числа: 567, 576, 657, 675, 756, 765.
Ответ: всего 6 чисел.
Контрольные вопросы
1. Какие типы обработки информации существуют?
2. Что такое граф?
3. Составьте граф, характеризующий тему «Животные».
4. Летом в лагере в одном отряде оказались пять девочек из Екатеринбурга, Саратова, Тулы, Иваново и Москвы: Маша, Даша, Лиза, Вика и Марина. На обед их посадили за один стол. Екатеринбурженка расположилась между москвичкой и Мариной, девочка из Саратова — между Машей и Дашей, а напротив оказались девочка из Иваново и Лиза. Вика не была в Саратове, а Маша никогда не была в Екатеринбурге и Москве, а москвичка с Дашей общаются в социальных сетях. Кто из какого города приехал в лагерь?
Вопрос 4
Маша приехала из Тулы, Даша из Екатеринбурга, Лиза из Москвы, Вика из Иваново и Марина приехала из Саратова.

