- Теорема о площади треугольника, описанного около окружности;
- Уточняющая теорема синусов и следствие из нее
- Формула Герона.
- Знать формулу площади треугольника, описанного около окружности;
- Уметь применять формулу площади треугольника, описанного около окружности;
- Уметь применять уточняющую теорему синусов и следствия из нее;
- Знать формулу Герона;
- Уметь применять формулу Герона при решении задач.
- Назовите известные вам формулы площади треугольника.
- Сформулируйте теорему синусов.
- Где лежит центр вписанной в треугольник окружности?
Теорема о площади треугольника, описанного около окружности
Площадь произвольного треугольника равна половине произведения стороны и высоты, опущенной на эту сторону, или . Это основная формула площади треугольника. Также площадь можно найти как половину произведения сторон и синуса угла между ними, или .
Треугольник имеет уникальную способность. В любой треугольник можно вписать окружность и любой треугольник можно вписать в окружность. Значит, можно предположить, что площадь треугольника можно выразить через радиусы описанной и вписанной окружностей.
Первая теорема связывает площадь треугольника и радиус вписанной окружности.
Теорема
Площадь треугольника выражается формулой
,
где - полупериметр треугольника, - радиус вписанной в него окружности.
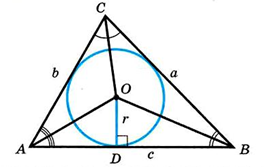 Рис. 1. Треугольник, описанный около окружности
Рис. 1. Треугольник, описанный около окружности
Доказательство этой теоремы очень простое.
Рассмотрим треугольник и вписанную в него окружность с центром в точке (рис. 1).
Так как окружность вписана, то все стороны треугольника являются касательными и радиусы, проведенные в точки касания, будут перпендикулярны сторонам.
Рассмотрим треугольники , и . Площадь каждого из них можно вычислить по основной формуле площади треугольника , где высотой каждого треугольника будет радиус вписанной окружности.
Площадь треугольника равна сумме площадей треугольников , и . Тогда получим
,
где .
Теорема доказана.
Пример 1
Гипотенуза прямоугольного треугольника равна 25, а высота, опущенная на гипотенузу равна 6,72. Радиус окружности, вписанной в треугольник, равен 3. Найдите периметр треугольника.
Решение
Из формулы выразим полупериметр:
.
Площадь треугольника равна половине произведения гипотенузы на высоту, т.е.
.
Тогда периметр треугольника равен
.
Ответ: 56.
Упражнение 1
1. Площадь треугольника равна 231, а радиус вписанной окружности равен 7. Найдите периметр этого треугольника.
2. Периметр треугольника равен 88, а радиус вписанной окружности равен 10. Найдите площадь этого треугольника.
Уточняющая теорема синусов
Теорема синусов говорит о том, что стороны треугольника пропорциональны синусам противолежащих углов. Это утверждение можно уточнить.
Теорема
В треугольнике имеют место равенства
,
где - радиус окружности, описанной около треугольника .
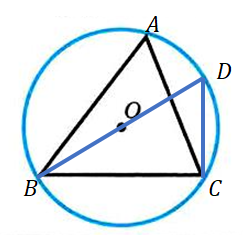 Рис. 2. Треугольник, вписанный в окружность
Рис. 2. Треугольник, вписанный в окружность
Рассмотрим треугольник и описанную около этого треугольника окружность с центром в точке (рис. 2).
Пусть угол - острый (в треугольнике есть хотя бы один острый угол). Проведем диаметр и хорду .
Углы и равны, так как являются вписанными углами, опирающимися на одну и ту же дугу . , так как опирается на диаметр.
Тогда применим теорему синусов для треугольника . Получим
.
Так как углы и равны, то
.
Последнее равенство описывает отношение стороны к синусу противолежащего угла в треугольнике . Следовательно, теорема доказана.
Данная теорема имеет два следствия, которые связывают площадь треугольника и радиус описанной окружности.
Следствие 1
Площадь треугольника со сторонами и выражается формулой
,
где - радиус описанной около него окружности.
Следствие 2
Площадь треугольника выражается формулой
,
где - радиус описанной около него окружности.
Следствия можно доказать, используя формулу , выразив синус угла через теорему синусов.
Формула Герона
Следующая формула площади треугольника одна из самых удобных. С помощью неё можно вычислить площадь треугольника, зная длины всех его сторон.
Формула Герона
Площадь треугольника со сторонами и можно вычислить по формуле
,
где - полупериметр треугольника.
Формулу можно доказать с помощью формулы . Для этого необходимо выразить через стороны треугольника, воспользовавшись теоремой косинусов и основным тригонометрическим тожеством.
Пример 2
Боковые стороны равнобедренного треугольника равны 5, основание равно 8. Найдите радиус окружности, описанной около этого треугольника.
Решение
С одной стороны, площадь треугольника можно вычислить по формуле Отсюда можно найти радиус описанной окружности:
.
С другой стороны, можно воспользоваться формулой Герона:
,
где .
Вычислим радиус
.
Ответ: .
Упражнение 2
1. Боковые стороны равнобедренного треугольника равны 13, основание равно 24. Найдите радиус окружности, описанной около этого треугольника.
2. Сторона треугольника равна 28. Противолежащий ей угол равен . Найдите радиус окружности, описанной около этого треугольника.
Контрольные вопросы
1. Как выразить площадь треугольника через радиус окружности, вписанной в этот треугольник?
2. Что нужно знать, чтобы вычислить площадь треугольника по формуле Герона?
Упражнение 1
1. 66.
2. 440.
Упражнение 2
1. 16,9.
2. 28.
- Теорема о площади треугольника, описанного около окружности;
- Уточняющая теорема синусов и следствие из нее
- Формула Герона.
- Знать формулу площади треугольника, описанного около окружности;
- Уметь применять формулу площади треугольника, описанного около окружности;
- Уметь применять уточняющую теорему синусов и следствия из нее;
- Знать формулу Герона;
- Уметь применять формулу Герона при решении задач.
- Назовите известные вам формулы площади треугольника.
- Сформулируйте теорему синусов.
- Где лежит центр вписанной в треугольник окружности?
Теорема о площади треугольника, описанного около окружности
Площадь произвольного треугольника равна половине произведения стороны и высоты, опущенной на эту сторону, или . Это основная формула площади треугольника. Также площадь можно найти как половину произведения сторон и синуса угла между ними, или .
Треугольник имеет уникальную способность. В любой треугольник можно вписать окружность и любой треугольник можно вписать в окружность. Значит, можно предположить, что площадь треугольника можно выразить через радиусы описанной и вписанной окружностей.
Первая теорема связывает площадь треугольника и радиус вписанной окружности.
Теорема
Площадь треугольника выражается формулой
,
где - полупериметр треугольника, - радиус вписанной в него окружности.
 Рис. 1. Треугольник, описанный около окружности
Рис. 1. Треугольник, описанный около окружности
Доказательство этой теоремы очень простое.
Рассмотрим треугольник и вписанную в него окружность с центром в точке (рис. 1).
Так как окружность вписана, то все стороны треугольника являются касательными и радиусы, проведенные в точки касания, будут перпендикулярны сторонам.
Рассмотрим треугольники , и . Площадь каждого из них можно вычислить по основной формуле площади треугольника , где высотой каждого треугольника будет радиус вписанной окружности.
Площадь треугольника равна сумме площадей треугольников , и . Тогда получим
,
где .
Теорема доказана.
Пример 1
Гипотенуза прямоугольного треугольника равна 25, а высота, опущенная на гипотенузу равна 6,72. Радиус окружности, вписанной в треугольник, равен 3. Найдите периметр треугольника.
Решение
Из формулы выразим полупериметр:
.
Площадь треугольника равна половине произведения гипотенузы на высоту, т.е.
.
Тогда периметр треугольника равен
.
Ответ: 56.
Упражнение 1
1. Площадь треугольника равна 231, а радиус вписанной окружности равен 7. Найдите периметр этого треугольника.
2. Периметр треугольника равен 88, а радиус вписанной окружности равен 10. Найдите площадь этого треугольника.
Уточняющая теорема синусов
Теорема синусов говорит о том, что стороны треугольника пропорциональны синусам противолежащих углов. Это утверждение можно уточнить.
Теорема
В треугольнике имеют место равенства
,
где - радиус окружности, описанной около треугольника .
 Рис. 2. Треугольник, вписанный в окружность
Рис. 2. Треугольник, вписанный в окружность
Рассмотрим треугольник и описанную около этого треугольника окружность с центром в точке (рис. 2).
Пусть угол - острый (в треугольнике есть хотя бы один острый угол). Проведем диаметр и хорду .
Углы и равны, так как являются вписанными углами, опирающимися на одну и ту же дугу . , так как опирается на диаметр.
Тогда применим теорему синусов для треугольника . Получим
.
Так как углы и равны, то
.
Последнее равенство описывает отношение стороны к синусу противолежащего угла в треугольнике . Следовательно, теорема доказана.
Данная теорема имеет два следствия, которые связывают площадь треугольника и радиус описанной окружности.
Следствие 1
Площадь треугольника со сторонами и выражается формулой
,
где - радиус описанной около него окружности.
Следствие 2
Площадь треугольника выражается формулой
,
где - радиус описанной около него окружности.
Следствия можно доказать, используя формулу , выразив синус угла через теорему синусов.
Формула Герона
Следующая формула площади треугольника одна из самых удобных. С помощью неё можно вычислить площадь треугольника, зная длины всех его сторон.
Формула Герона
Площадь треугольника со сторонами и можно вычислить по формуле
,
где - полупериметр треугольника.
Формулу можно доказать с помощью формулы . Для этого необходимо выразить через стороны треугольника, воспользовавшись теоремой косинусов и основным тригонометрическим тожеством.
Пример 2
Боковые стороны равнобедренного треугольника равны 5, основание равно 8. Найдите радиус окружности, описанной около этого треугольника.
Решение
С одной стороны, площадь треугольника можно вычислить по формуле Отсюда можно найти радиус описанной окружности:
.
С другой стороны, можно воспользоваться формулой Герона:
,
где .
Вычислим радиус
.
Ответ: .
Упражнение 2
1. Боковые стороны равнобедренного треугольника равны 13, основание равно 24. Найдите радиус окружности, описанной около этого треугольника.
2. Сторона треугольника равна 28. Противолежащий ей угол равен . Найдите радиус окружности, описанной около этого треугольника.
Контрольные вопросы
1. Как выразить площадь треугольника через радиус окружности, вписанной в этот треугольник?
2. Что нужно знать, чтобы вычислить площадь треугольника по формуле Герона?
Упражнение 1
1. 66.
2. 440.
Упражнение 2
1. 16,9.
2. 28.


