- Теорема о медиане треугольника;
- Следствие о диагоналях параллелограмма;
- Примеры.
- Знать формулу нахождения длины медианы треугольника;
- Знать формулу связи длин диагоналей и сторон параллелограмма;
- Уметь применять указанные формулы при решении задач.
- Что называют медианой треугольника?
- Какими свойствами обладает медиана треугольника?
- Диагонали какого четырехугольника точкой пересечения делятся пополам?
Теорема о медиане треугольника
Из курса планиметрии известно, что по известным трем элементам треугольника можно найти другие его элементы. Вспомним некоторые определения и теоремы.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
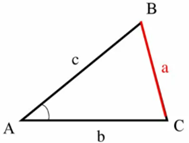 Рис. 1. Теорема косинусов
Рис. 1. Теорема косинусов
Для доказательства следующей теоремы понадобится теорема косинусов (рис. 1):
.
Длину медианы любого треугольника можно найти, зная длины его сторон.
Теорема
Квадрат медианы треугольника выражается формулой
.
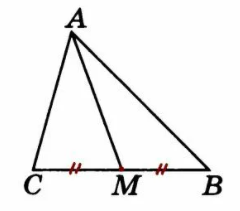 Рис. 2. Теорема о медиане треугольника
Рис. 2. Теорема о медиане треугольника
Рассмотрим треугольник , где - медиана (рис. 2).
Длину этой медианы можно найти по теореме косинусов в треугольнике , тогда
.
Используя теорему косинусов для треугольника , выразим косинус угла :
,
тогда
.
Так как - медиана треугольника, то . Подставим полученные соотношения в выражения для :
.
Теорема доказана.
Пример 1
В прямоугольном треугольнике , , . Найти длину медианы .
Решение
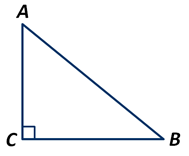 Рис. 3. Прямоугольный треугольник ABC
Рис. 3. Прямоугольный треугольник ABC
Сначала найдем длину гипотенузы по теореме Пифагора:
.
Воспользуемся теоремой о медиане треугольника:
.
т.е.
.
Ответ: 5.
Упражнение 1
1. Стороны треугольника равны 4, 6, 8. Найдите длину медианы, проведенную к меньшей стороне.
2. Найди длину основания равнобедренного треугольника, если боковая сторона равна 2, а медиана, проведенная к боковой стороне, равна .
Следствие о диагоналях параллелограмма
Доказанная выше теорема имеет следствие. Но сначала вспомним, что диагонали параллелограмма точкой пересечения делятся пополам.
Следствие
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
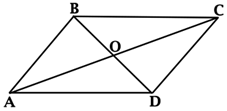 Рис. 4. Следствие о диагоналях параллелограмма
Рис. 4. Следствие о диагоналях параллелограмма
Рассмотрим параллелограмм (рис. 4).
Так как диагонали параллелограмма точкой пересечения делятся пополам, то - медиана треугольника . Тогда, используя, предыдущую теорему, получаем
,
или
.
Умножим обе части выражения на 4 и перенесём квадрат диагонали в левую часть. Получили
.
Значит, .
Следствие доказано.
Пример 2
Диагонали ромба равны 5 и 12. Найти длину стороны ромба.
Решение
Ромб – это параллелограмм, стороны которого равны. Значит, сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Пусть сторона равна , а диагонали равны и . Тогда
.
или
.
Ответ: 6,5.
Упражнение 2
Стороны параллелограмма равны 4 и 5, а одна из его диагоналей равна 7. Найти длину другой диагонали параллелограмма.
Контрольные вопросы
1. Сформулируйте теорему о медиане треугольника.
2. Может ли быть медиана больше каждой из сторон треугольника? Почему?
Упражнение 1
1. ;
2. 1.
Упражнение 2
.
- Теорема о медиане треугольника;
- Следствие о диагоналях параллелограмма;
- Примеры.
- Знать формулу нахождения длины медианы треугольника;
- Знать формулу связи длин диагоналей и сторон параллелограмма;
- Уметь применять указанные формулы при решении задач.
- Что называют медианой треугольника?
- Какими свойствами обладает медиана треугольника?
- Диагонали какого четырехугольника точкой пересечения делятся пополам?
Теорема о медиане треугольника
Из курса планиметрии известно, что по известным трем элементам треугольника можно найти другие его элементы. Вспомним некоторые определения и теоремы.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
 Рис. 1. Теорема косинусов
Рис. 1. Теорема косинусов
Для доказательства следующей теоремы понадобится теорема косинусов (рис. 1):
.
Длину медианы любого треугольника можно найти, зная длины его сторон.
Теорема
Квадрат медианы треугольника выражается формулой
.
 Рис. 2. Теорема о медиане треугольника
Рис. 2. Теорема о медиане треугольника
Рассмотрим треугольник , где - медиана (рис. 2).
Длину этой медианы можно найти по теореме косинусов в треугольнике , тогда
.
Используя теорему косинусов для треугольника , выразим косинус угла :
,
тогда
.
Так как - медиана треугольника, то . Подставим полученные соотношения в выражения для :
.
Теорема доказана.
Пример 1
В прямоугольном треугольнике , , . Найти длину медианы .
Решение
 Рис. 3. Прямоугольный треугольник ABC
Рис. 3. Прямоугольный треугольник ABC
Сначала найдем длину гипотенузы по теореме Пифагора:
.
Воспользуемся теоремой о медиане треугольника:
.
т.е.
.
Ответ: 5.
Упражнение 1
1. Стороны треугольника равны 4, 6, 8. Найдите длину медианы, проведенную к меньшей стороне.
2. Найди длину основания равнобедренного треугольника, если боковая сторона равна 2, а медиана, проведенная к боковой стороне, равна .
Следствие о диагоналях параллелограмма
Доказанная выше теорема имеет следствие. Но сначала вспомним, что диагонали параллелограмма точкой пересечения делятся пополам.
Следствие
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
 Рис. 4. Следствие о диагоналях параллелограмма
Рис. 4. Следствие о диагоналях параллелограмма
Рассмотрим параллелограмм (рис. 4).
Так как диагонали параллелограмма точкой пересечения делятся пополам, то - медиана треугольника . Тогда, используя, предыдущую теорему, получаем
,
или
.
Умножим обе части выражения на 4 и перенесём квадрат диагонали в левую часть. Получили
.
Значит, .
Следствие доказано.
Пример 2
Диагонали ромба равны 5 и 12. Найти длину стороны ромба.
Решение
Ромб – это параллелограмм, стороны которого равны. Значит, сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Пусть сторона равна , а диагонали равны и . Тогда
.
или
.
Ответ: 6,5.
Упражнение 2
Стороны параллелограмма равны 4 и 5, а одна из его диагоналей равна 7. Найти длину другой диагонали параллелограмма.
Контрольные вопросы
1. Сформулируйте теорему о медиане треугольника.
2. Может ли быть медиана больше каждой из сторон треугольника? Почему?
Упражнение 1
1. ;
2. 1.
Упражнение 2
.


