Все уроки по всем предметам школьной программы ФГОС

Теорема о биссектрисе треугольника

План урока

Теорема о биссектрисе треугольника;
Следствие о длине отрезков, на которые биссектриса делит сторону;
Длина биссектрисы.

Цели урока

Знать свойство биссектрисы треугольника;
Уметь находить длины отрезков, на которые биссектриса делит сторону;
Уметь находить длину биссектрисы.

Разминка

Что такое биссектриса треугольника?
Что вы знаете о биссектрисе равнобедренного треугольника, проведенной к его основанию?
Как найти длину биссектрисы равностороннего треугольника?

Теорема о биссектрисе треугольника

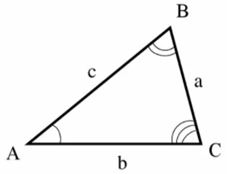Рис. 1. Теорема синусов

Вспомним, что биссектрисой треугольника называют отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Также вспомним теорему синусов: стороны треугольника пропорциональны синусам противолежащих углов (рис. 1), т.е.

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ .

Следующая теорема является свойством биссектрисы треугольника.

Теорема

Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам.

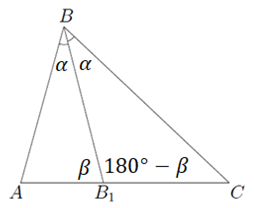Рис. 2. Теорема о биссектрисе треугольника

Рассмотрим треугольник $A B C$ , где $B B_{1}$ - биссектриса (рис. 2).

Введем обозначения. Так как $B B_{1}$ - биссектриса, то $∠ A B B_{1} = ∠ C B B_{1}$ . Обозначим их градусные меры $α$ . Углы $∠ A B_{1} B$ и $∠ C B_{1} B$ смежные, тогда пусть $∠ A B_{1} B = β$ , $∠ C B_{1} B = 180 ° - β$ .

По теореме синусов в треугольнике $A B B_{1}$

$\frac{A B_{1}}{s i n α} = \frac{A B}{s i n β}$ , $\frac{A B_{1}}{A B} = \frac{\sin α}{s i n β}$ .

Аналогично, в треугольнике $C B B_{1}$ получим

$\frac{C B_{1}}{s i n α} = \frac{C B}{s i n (180 ° - β)}$ , $\frac{C B_{1}}{C B} = \frac{\sin α}{s i n (180 ° - β)}$ .

Так как синусы смежных углов равны, то имеем, что $\sin β = \sin (180 ° - β)$ .

Тогда можем приравнять левые части полученных соотношений для треугольников $A B B_{1}$ и $C B B_{1}$ :

$\frac{A B_{1}}{A B} = \frac{C B_{1}}{C B}$ ,

откуда

$\frac{A B_{1}}{C B_{1}} = \frac{A B}{C B}$ .

Пример 1

В треугольнике $A B C$ проведена биссектриса $A D$ (рис. 3). Найдите периметр треугольника $A B C$ , если $А С = 4$ , $D C = 2$ , $B D = 3$ .

Решение

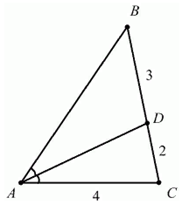Рис. 3. Треугольник ABC

Периметр треугольника – это сумма длин всех его сторон.

Используя соотношение из теоремы о биссектрисе треугольника, найдем длину стороны $A B$ :

$\frac{D C}{D B} = \frac{A C}{A B}$ ,

$A B = \frac{A C \cdot D B}{D C} = \frac{4 \cdot 3}{2} = 6$ .

Тогда

$P_{A B C} = 4 + 6 + (2 + 3) = 15$ .

Ответ: 15.

Упражнение 1

В треугольнике $A B C$ проведена биссектриса $A D$ . Найдите периметр треугольника $A B C$ , если $А С = 6$ , $D C = 3$ , $B D = 4$ .

Следствие из теоремы

Раз биссектриса делит сторону на части, пропорциональные другим сторонам, то длины этих частей можно найти, зная стороны треугольника.

Вернемся к треугольнику $A B C$ (рис. 2). Нам известно, что

$\frac{A B_{1}}{C B_{1}} = \frac{A B}{C B}$

или

$A B_{1} \cdot C B = A B \cdot C B_{1}$ .

С другой стороны, $A B_{1} + C B_{1} = A C$ . Выразим из этих двух равенств $A B_{1}$ , получим

$(A C - C B_{1}) \cdot C B = A B \cdot C B_{1}$ ,

$C B_{1} = \frac{A C \cdot C B}{A B + C B}$ .

Аналогично можно получить, что

$A B_{1} = \frac{A C \cdot A B}{A B + C B}$ .

Таким образом, мы выразили длины отрезков, на которые биссектриса делит сторону, через длины сторон треугольника.

Следствие

В треугольнике $A B C$ со сторонами $A B = c, A C = b, B C = a$ и биссектрисой $B B_{1}$ имеют место равенства:

$C B_{1} = \frac{a b}{a + c}$ , $A B_{1} = \frac{b c}{a + c}$ .

Формула длины биссектрисы

Биссектриса является отрезком треугольника, значит, её длину можно найти, зная длины сторон треугольника.

На самом деле длина биссектрисы выражается через стороны, образующие угол, и через длины отрезков, на которые биссектриса делит оставшуюся сторону.

В треугольнике $A B C$ со сторонами $A B = c, B C = a$ длину биссектрисы $B B_{1}$ можно вычислить по формуле:

$B B_{1}^{2} = a c - A B_{1} \cdot C B_{1}$ .

Пример 2

Стороны треугольника равны 5, 7 и 10. Найдите длину биссектрисы, проведенную к большей стороне.

Решение

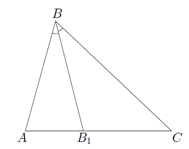Рис. 4. Треугольник ABC

Рассмотрим треугольник $A B C$ (рис. 4). Пусть $A B = 5$ , $B C = 7$ , и $A C = 10$ .

Найдем длины отрезков $A B_{1}$ и $B_{1} C$ :

$A B_{1} = \frac{A C \cdot A B}{A B + B C} = \frac{10 \cdot 5}{5 + 7} = \frac{25}{6}$ ,

$B_{1} C = A C - A B_{1} = \frac{35}{6}$ .

Найдем длину биссектрисы:

$B B_{1} = \sqrt{A B \cdot B C - A B_{1} \cdot C B_{1}} = \sqrt{5 \cdot 7 - \frac{25}{6} \cdot \frac{35}{6}} = \sqrt{\frac{385}{6}}$ .

Ответ: $\sqrt{\frac{385}{6}}$ .

Упражнение 2

Стороны треугольника равны 4, 7, 9. Найти длину биссектрисы, проведенной к меньшей стороне.

Контрольные вопросы

1. Сформулируйте теорему о биссектрисе треугольника.

2. Как найти длину биссектрисы треугольника?

Ответы

Упражнение 1

21.

Упражнение 2

$\frac{3 \sqrt{105}}{4}$ .

Конспект урока: Теорема о биссектрисе треугольника

Треугольники

Теорема о биссектрисе треугольника

Следствие из теоремы

Формула длины биссектрисы