- Закон всемирного тяготения
- Примеры решения задач
- знать понятия: гравитационные силы, первая космическая скорость; формулировку закона всемирного тяготения
- уметь объяснять, от каких величин зависит сила притяжения; использовать второй закон Ньютона для расчёта описания характера движения планет вокруг Солнца, спутников вокруг Земли
- Действие какой силы обуславливает движение Земли вокруг Солнца?
- Как направлена равнодействующая сил, действующих на Землю, в системе отсчёта, связанной с Солнцем?
- Как направлена мгновенная скорость планет при их движении вокруг Солнца?
Закон всемирного тяготения
Известно, что Земля притягивает к себе все тела, находящиеся на её поверхности с силой тяжести . Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести
.
В 1685 г. Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
Исследования характера движения планет вокруг Солнца позволили Ньютону определить зависимость между силой, с которой притягиваются все тела во Вселенной, их массой и расстоянием и в 1687 г. сформулировать закон всемирного тяготения:
,
F [Н] — сила тяготения между двумя телами;
G = 6,67 ∙ 10-11 Н ∙ м2/кг2 — гравитационная постоянная;
m1 и m2 [кг] — массы первого и второго тела соответственно;
R [м] — расстояние между телами.
Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
Гравитационная постоянная G — это коэффициент, одинаковый для любой пары взаимодействующих тел. Более чем через сто лет после открытия Ньютоном закона всемирного тяготения английский физик Генри Кавендиш смог экспериментально измерить значение гравитационной постоянной G. Опытным путём Каведиш получил то же значение гравитационной постоянной, что и Ньютон: G = 6,67 ∙ 10-11 Н ∙ м2/кг2.
Закон всемирного тяготения применим только к телам, расстояние между которыми во много раз больше размеров самих тел. Для тел, имеющих форму шара, величина R соответствует расстоянию между центрами данных шаров. Для тел иной формы закон всемирного тяготения также применим, но требует более сложных математических расчётов.
Для описания характера движения спутников планет систему отсчёта связывают с планетой, вокруг которой вращается спутник. Например, при рассмотрении Луны удобно использовать геоцентрическую систему отсчёта, она тоже является инерциальной. Началом отсчёта геоцентрической системы является центр Земли. Луна движется по эллиптической орбите, но при решении задач также можно принять допущение, что спутник равномерно движется по окружности вокруг планеты. Аналогично для описания характера движения планет вокруг Солнца систему отсчёта связывают с центром звезды — используют гелиоцентрическую систему отсчёта. Рассмотрим несколько примеров задач.
Примеры решения задач
Пример 1
Известно, что период обращения Венеры вокруг Солнца равен T = 0,62 земного года, а среднее расстояние до Солнца 0,7 а. е. На основании этих данных рассчитайте массу Солнца.
Решение
1. Расстояние между Венерой и Солнцем во много раз больше размеров рассматриваемых небесных тел, поэтому их можно принять за материальные точки.
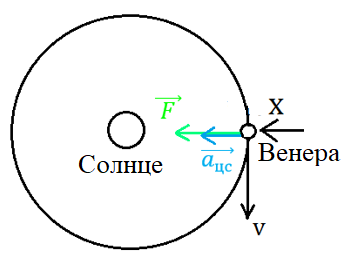 Рис. 1. Направление скорости и ускорения Венеры в системе отсчёта, связанной с Солнцем
Рис. 1. Направление скорости и ускорения Венеры в системе отсчёта, связанной с Солнцем
2. В качестве тела отсчёта выберем Солнце. Координатная ось ОХ направлена к центру звезды (рис. 1).
На Венеру действует только сила притяжения F со стороны Солнца, скорость спутника направлена по касательной, центростремительное ускорение — к центру звезды.
3. Второй закон Ньютона в векторной форме для планеты имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на ось ОХ:
.
5. Используем формулы для расчёта силы притяжения Земли и центростремительного ускорения:
.
где R — среднее расстояние между центрами Венеры и Солнца (средний радиус орбиты планеты).
Учтём, что период движения тела по окружности вычисляется по формуле:
.
Выразим из формулы выше скорость движения планеты:
.
Подставим это выражение для скорости в формулу .
Сократим обе части на массу Венеры mВ и средний радиус орбиты R. Из полученного выражения выразим искомую массу Солнца:
;
.
Заметим, что по условию задачи расстояние между Венерой и Солнцем указано в а. е. — астрономической единице. Астрономическая
единица — это среднее расстояние от Земли до Солнца, равное примерно м.
.
Ответ: .
Преобразуем выражение:
.
Из этого соотношения следует, что отношение куба радиуса орбиты планеты к квадрату периода её обращения вокруг Солнца не зависит от массы самой планеты, а зависит только от массы звезды. Следовательно, отношение справедливо для всех планет Солнечной системы.
Данное соотношение было получено немецким астрономом Иоганном Кеплером (1571–1630) ещё до открытия закона всемирного тяготения. Полученное учёным соотношение называется третьим законом Кеплера.
Пример 2
Рассчитайте скорость и период обращения Луны в системе отсчёта, связанной с Землёй.
Решение
1. Расстояние между Луной и Землёй во много раз больше размеров рассматриваемых небесных тел, поэтому их можно принять за материальные точки.
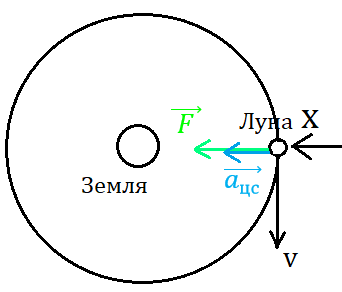 Рис. 2. Направление скорости и ускорения Луны в системе отсчёта, связанной с Землёй
Рис. 2. Направление скорости и ускорения Луны в системе отсчёта, связанной с Землёй
2. В качестве тела отсчёта выберем Землю. Координатная ось ОХ направлена к центру планеты (рис. 2). На Луну действует только сила притяжения F со стороны Земли, скорость спутника направлена по касательной, центростремительное ускорение —
к центру Земли.
3. Второй закон Ньютона в векторной форме для Луны имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на ось ОХ:
.
5. Используем формулы для расчёта силы притяжения Земли и центростремительного ускорения:
,
где R — среднее расстояние между центрами Луны и Земли.
Выражаем искомую скорость:
.
Среднее расстояние между центрами Земли и Луны составляет 384,4 ∙ 106 м. Масса Земли равна 5,97 ∙ 1024 кг.
.
6. Находим период обращения Луны:
;
.
Ответ: ; .
Обратим внимание на формулы: ни скорость Луны при движении по орбите, ни период её обращения вокруг Земли не зависят от массы самого спутника.
Таким образом, на расстоянии R, равном расстоянию между центрами Земли и Луны, любое тело будет двигаться со скоростью = 1 км/с и периодом обращения
Т = 27 суток.
Скорость и период этого тела будут зависеть только от расстояния до Земли и её массы.
Таким образом, скорость движения спутника по орбите вокруг Земли не зависит от массы спутника, а определяется радиусом орбиты его вращения: чем больше высота над поверхностью Земли, на которой находится спутник, тем меньше скорость его обращения вокруг планеты. Чтобы запустить искусственный спутник на орбиту планеты, необходимо сообщить ему некоторую минимальную скорость, называемую первой космической скоростью. Первую космическую скорость можно вычислить по формуле
,
где m [кг] — масса планеты;
R [м] — радиус планеты.
Модуль скорости, которую необходимо сообщить телу, чтобы оно стало двигаться по круговой орбите вокруг Земли вблизи её поверхности только под действием силы притяжения Земли, называется первой космической скоростью : .
Рассчитаем первую космическую скорость для Земли:
.
Итоги
- Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
- Закон всемирного тяготения: две материальные точки массами и притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
- Минимальная горизонтальная скорость, которую необходимо придать телу, чтобы оно совершало движение по круговой орбите вокруг планеты, называется первой космической скоростью: .
- Первая космическая скорость Земли равна .
Упражнение 1
1. Как изменится центростремительное ускорение, скорость и период обращения спутника при его переходе на орбиту большего радиуса?
2. Рассчитайте первую космическую скорость Венеры. Масса Венеры равна кг, а средний радиус — км.
3. Определите период обращения Марса вокруг Солнца. Масса солнца равна кг, среднее расстояние от Марса до Солнца составляет
а. е.
Контрольные вопросы
1. Сформулируйте закон всемирного тяготения.
2. От чего зависит скорость движения спутника по орбите планеты?
3. Что такое первая космическая скорость?
Упражнение 1
1. Центростремительное ускорение уменьшится; скорость уменьшится; период обращения увеличится.
2. км/с
3. Т = 1,88 года
- Закон всемирного тяготения
- Примеры решения задач
- знать понятия: гравитационные силы, первая космическая скорость; формулировку закона всемирного тяготения
- уметь объяснять, от каких величин зависит сила притяжения; использовать второй закон Ньютона для расчёта описания характера движения планет вокруг Солнца, спутников вокруг Земли
- Действие какой силы обуславливает движение Земли вокруг Солнца?
- Как направлена равнодействующая сил, действующих на Землю, в системе отсчёта, связанной с Солнцем?
- Как направлена мгновенная скорость планет при их движении вокруг Солнца?
Закон всемирного тяготения
Известно, что Земля притягивает к себе все тела, находящиеся на её поверхности с силой тяжести . Согласно третьему закону Ньютона, тело, в свою очередь, тоже будет притягивать к себе Землю с силой, равной по модулю силе тяжести
.
В 1685 г. Исаак Ньютон предположил, что силы притяжения существуют между всеми телами во Вселенной.
Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
Исследования характера движения планет вокруг Солнца позволили Ньютону определить зависимость между силой, с которой притягиваются все тела во Вселенной, их массой и расстоянием и в 1687 г. сформулировать закон всемирного тяготения:
,
F [Н] — сила тяготения между двумя телами;
G = 6,67 ∙ 10-11 Н ∙ м2/кг2 — гравитационная постоянная;
m1 и m2 [кг] — массы первого и второго тела соответственно;
R [м] — расстояние между телами.
Закон всемирного тяготения: две материальные точки массами m1 и m2 притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
Гравитационная постоянная G — это коэффициент, одинаковый для любой пары взаимодействующих тел. Более чем через сто лет после открытия Ньютоном закона всемирного тяготения английский физик Генри Кавендиш смог экспериментально измерить значение гравитационной постоянной G. Опытным путём Каведиш получил то же значение гравитационной постоянной, что и Ньютон: G = 6,67 ∙ 10-11 Н ∙ м2/кг2.
Закон всемирного тяготения применим только к телам, расстояние между которыми во много раз больше размеров самих тел. Для тел, имеющих форму шара, величина R соответствует расстоянию между центрами данных шаров. Для тел иной формы закон всемирного тяготения также применим, но требует более сложных математических расчётов.
Для описания характера движения спутников планет систему отсчёта связывают с планетой, вокруг которой вращается спутник. Например, при рассмотрении Луны удобно использовать геоцентрическую систему отсчёта, она тоже является инерциальной. Началом отсчёта геоцентрической системы является центр Земли. Луна движется по эллиптической орбите, но при решении задач также можно принять допущение, что спутник равномерно движется по окружности вокруг планеты. Аналогично для описания характера движения планет вокруг Солнца систему отсчёта связывают с центром звезды — используют гелиоцентрическую систему отсчёта. Рассмотрим несколько примеров задач.
Примеры решения задач
Пример 1
Известно, что период обращения Венеры вокруг Солнца равен T = 0,62 земного года, а среднее расстояние до Солнца 0,7 а. е. На основании этих данных рассчитайте массу Солнца.
Решение
1. Расстояние между Венерой и Солнцем во много раз больше размеров рассматриваемых небесных тел, поэтому их можно принять за материальные точки.
 Рис. 1. Направление скорости и ускорения Венеры в системе отсчёта, связанной с Солнцем
Рис. 1. Направление скорости и ускорения Венеры в системе отсчёта, связанной с Солнцем
2. В качестве тела отсчёта выберем Солнце. Координатная ось ОХ направлена к центру звезды (рис. 1).
На Венеру действует только сила притяжения F со стороны Солнца, скорость спутника направлена по касательной, центростремительное ускорение — к центру звезды.
3. Второй закон Ньютона в векторной форме для планеты имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на ось ОХ:
.
5. Используем формулы для расчёта силы притяжения Земли и центростремительного ускорения:
.
где R — среднее расстояние между центрами Венеры и Солнца (средний радиус орбиты планеты).
Учтём, что период движения тела по окружности вычисляется по формуле:
.
Выразим из формулы выше скорость движения планеты:
.
Подставим это выражение для скорости в формулу .
Сократим обе части на массу Венеры mВ и средний радиус орбиты R. Из полученного выражения выразим искомую массу Солнца:
;
.
Заметим, что по условию задачи расстояние между Венерой и Солнцем указано в а. е. — астрономической единице. Астрономическая
единица — это среднее расстояние от Земли до Солнца, равное примерно м.
.
Ответ: .
Преобразуем выражение:
.
Из этого соотношения следует, что отношение куба радиуса орбиты планеты к квадрату периода её обращения вокруг Солнца не зависит от массы самой планеты, а зависит только от массы звезды. Следовательно, отношение справедливо для всех планет Солнечной системы.
Данное соотношение было получено немецким астрономом Иоганном Кеплером (1571–1630) ещё до открытия закона всемирного тяготения. Полученное учёным соотношение называется третьим законом Кеплера.
Пример 2
Рассчитайте скорость и период обращения Луны в системе отсчёта, связанной с Землёй.
Решение
1. Расстояние между Луной и Землёй во много раз больше размеров рассматриваемых небесных тел, поэтому их можно принять за материальные точки.
 Рис. 2. Направление скорости и ускорения Луны в системе отсчёта, связанной с Землёй
Рис. 2. Направление скорости и ускорения Луны в системе отсчёта, связанной с Землёй
2. В качестве тела отсчёта выберем Землю. Координатная ось ОХ направлена к центру планеты (рис. 2). На Луну действует только сила притяжения F со стороны Земли, скорость спутника направлена по касательной, центростремительное ускорение —
к центру Земли.
3. Второй закон Ньютона в векторной форме для Луны имеет следующий вид:
.
4. Запишем второй закон Ньютона в проекциях на ось ОХ:
.
5. Используем формулы для расчёта силы притяжения Земли и центростремительного ускорения:
,
где R — среднее расстояние между центрами Луны и Земли.
Выражаем искомую скорость:
.
Среднее расстояние между центрами Земли и Луны составляет 384,4 ∙ 106 м. Масса Земли равна 5,97 ∙ 1024 кг.
.
6. Находим период обращения Луны:
;
.
Ответ: ; .
Обратим внимание на формулы: ни скорость Луны при движении по орбите, ни период её обращения вокруг Земли не зависят от массы самого спутника.
Таким образом, на расстоянии R, равном расстоянию между центрами Земли и Луны, любое тело будет двигаться со скоростью = 1 км/с и периодом обращения
Т = 27 суток.
Скорость и период этого тела будут зависеть только от расстояния до Земли и её массы.
Таким образом, скорость движения спутника по орбите вокруг Земли не зависит от массы спутника, а определяется радиусом орбиты его вращения: чем больше высота над поверхностью Земли, на которой находится спутник, тем меньше скорость его обращения вокруг планеты. Чтобы запустить искусственный спутник на орбиту планеты, необходимо сообщить ему некоторую минимальную скорость, называемую первой космической скоростью. Первую космическую скорость можно вычислить по формуле
,
где m [кг] — масса планеты;
R [м] — радиус планеты.
Модуль скорости, которую необходимо сообщить телу, чтобы оно стало двигаться по круговой орбите вокруг Земли вблизи её поверхности только под действием силы притяжения Земли, называется первой космической скоростью : .
Рассчитаем первую космическую скорость для Земли:
.
Итоги
- Все тела во Вселенной притягиваются друг к другу с силами, которые называются силами всемирного тяготения или гравитационными силами.
- Закон всемирного тяготения: две материальные точки массами и притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: .
- Минимальная горизонтальная скорость, которую необходимо придать телу, чтобы оно совершало движение по круговой орбите вокруг планеты, называется первой космической скоростью: .
- Первая космическая скорость Земли равна .
Упражнение 1
1. Как изменится центростремительное ускорение, скорость и период обращения спутника при его переходе на орбиту большего радиуса?
2. Рассчитайте первую космическую скорость Венеры. Масса Венеры равна кг, а средний радиус — км.
3. Определите период обращения Марса вокруг Солнца. Масса солнца равна кг, среднее расстояние от Марса до Солнца составляет
а. е.
Контрольные вопросы
1. Сформулируйте закон всемирного тяготения.
2. От чего зависит скорость движения спутника по орбите планеты?
3. Что такое первая космическая скорость?
Упражнение 1
1. Центростремительное ускорение уменьшится; скорость уменьшится; период обращения увеличится.
2. км/с
3. Т = 1,88 года



