- Принцип относительности Галилея. Инерциальные и неинерциальные системы отсчёта
- знать формулировку принципа относительности Галилея; понятия: инерциальная и неинерциальная системы отсчёта, сила инерции
- уметь отличать инерциальные и неинерциальные системы отсчёта; описывать движение тела в неинерциальной системе отсчёта; объяснять физические явления с учётом существования сил инерции
- Сформулируйте закон сложения скоростей.
- Что такое сила инерции?
- Как описать движение тела в неинерциальной системе отсчёта?
Принцип относительности Галилея. Инерциальные и неинерциальные системы отсчёта
В предыдущих параграфах мы описывали характер движения тел относительно лабораторных систем отсчёта, связанных с Землей, то есть относительно инерциальных систем отсчёта. В данном параграфе мы рассмотрим, как описывается характер движения тела в неинерциальных системах отсчёта и выясним, применимы ли законы динамики в этом случае.
Пусть некоторое тело движется как в подвижной системе отсчёта, так и в неподвижной. Относительно ИСО скорость тела постоянна и равна . Относительно подвижной системы отсчёта данное тело движется со скоростью
, скорость подвижной системы отсчёта относительно ИСО равна . Тогда согласно закону сложения скоростей, изученному нами ранее, скорость тела в ИСО . Отсюда получаем, что скорость рассматриваемого тела относительно подвижной системы отсчёта . Из полученной разности следует, что подвижная система отсчёта также будет инерциальной.
Любая система, которая движется относительно данной инерциальной системы отсчёта равномерно и прямолинейно, является инерциальной.
Галилей установил, что характер движения и взаимодействия тел при рассмотрении в различных ИСО не изменяется. Это значит, что равномерное движение относительно Земли не влияет на протекание механических явлений. Представим ситуацию: вы находитесь в вагоне поезда, движущегося равномерно прямолинейно, никаких вибраций и тряски нет. Если в таких условиях подбросить мяч вверх или под углом к горизонту, он будет двигаться точно также, как если проделать эти действия на Земле. Если окна вагона зашторены, невозможно определить, движется ли поезд или находится в состоянии покоя относительно Земли. Результаты подобных экспериментов позволили сформулировать фундаментальный закон природы — принцип относительности Галилея.
Принцип относительности Галилея: при одинаковых начальных условиях все механические процессы протекают одинаково во всех инерциальных системах отсчёта.
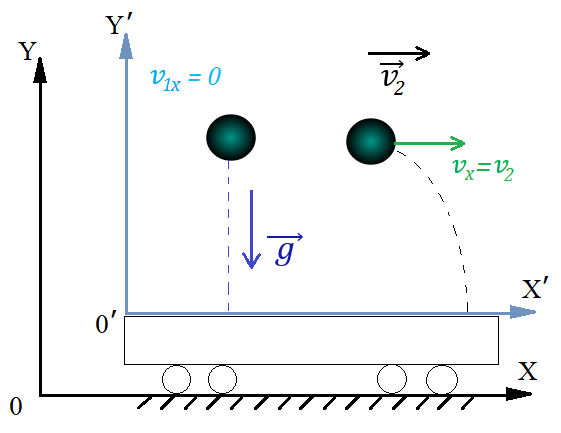 Рис. 1. Движение мячика в ИСО и НИСО
Рис. 1. Движение мячика в ИСО и НИСО
Иначе говоря, законы динамики имеют одинаковый вид во всех ИСО. Следует понимать, что иметь один и тот же вид будут только законы динамики, так как координаты и скорости тел относительно разных систем отсчёта различны, законы движения тел будут отличаться.
Например, находясь в вагоне поезда, движущегося равномерно прямолинейно относительно Земли, отпустим из рук удерживаемый на некоторой высоте мячик.
Вагон представляет собой подвижную систему отсчёта 0’X’Y’ (рис. 1). Относительно вагона проекция скорости мячика на ось 0’X’ в начальный момент времени равна нулю = 0, поэтому в данной системе отсчёта мячик будет свободно падать вертикально вниз.
В то же время относительно неподвижной системы отсчёта 0XY, связанной с Землёй, начальная скорость мячика равна скорости подвижной системы
отсчёта — движущегося вагона поезда. Проекция начальной скорости тела на ось абсцисс в данной системе отсчёта . Траектория движения мячика будет соответствовать траектории тела, брошенного горизонтально, — будет иметь форму параболы.
Таким образом, в приведённом примере законы динамики, описывающие движение мячика, будут иметь одинаковый вид в обеих системах отсчёта, но законы движения будут различны.
Для описания движения тела в подобных случаях используют так называемое преобразование Галилея. Если в рассматриваемой ИСО закон движения материальной точки имеет вид , то в другой ИСО, движущейся поступательно со скоростью относительно данной ИСО, закон движения данной точки выглядит следующим образом:
.
Если в приведённом выше примере поезд приобретёт некоторое ускорение относительно Земли — начнёт разгоняться или тормозить, наблюдатель в вагоне поезда сможет заметить это по изменениям в характере движения окружающих его тел. Так, при торможении поезда тела, находящиеся в вагоне, приобретут ускорение относительно вагона: например, находящиеся на столе предметы придут в движение относительно стола, несмотря на отсутствие действия на них других тел. Следовательно, если движущаяся относительно Земли система отсчёта приобретает ускорение, она перестаёт быть инерциальной и становится неинерциальной.
В неинерциальных системах отсчёта (НИСО) тела приобретают ускорение в отсутствие действия на них других тел.
В НИСО сумма всех сил , действующих на материальную точку, не равна произведению её массы m на ускорение в данной НИСО.
Тот факт, что в НИСО не выполняется равенство , позволяет отличать НИСО от ИСО экспериментально. Например, установлено, что в Южном полушарии нашей планеты у текущих в направлении меридиана рек левый берег выше правого, так как левый берег сильнее подмывается течением. Данное явление получило название закон Бэра в честь учёного, описавшего его в работе под названием «О всеобщем законе образования речных русел». Бэр объяснил асимметрию склонов речных долин вращением Земли вокруг своей оси. Отсюда следует вывод, что лабораторная система отсчёта, связанная с Землёй, является инерциальной лишь приближённо.
Рассмотрим, как записываются уравнения движения в НИСО в случае, если НИСО движется поступательно прямолинейно с ускорением относительно ИСО.
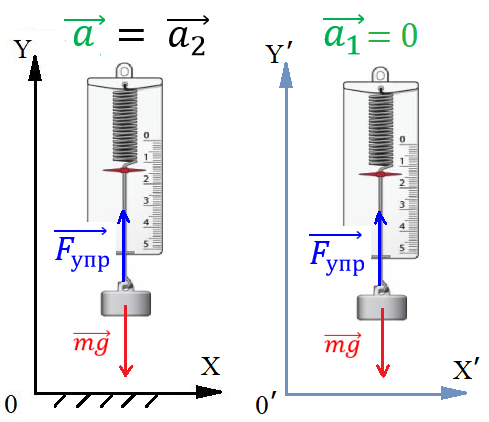 Рис. 2. Ускорение тела в ИСО и в НИСО
Рис. 2. Ускорение тела в ИСО и в НИСО
Пусть на динамометре висит груз массой m, а динамометр закреплён на потолке лифта. Лифт поднимается в шахте с ускорением (рис. 2).
Опишем движение груза в ИСО, связанной с неподвижной шахтой лифта, и в НИСО, связанной с ускоряющимся относительно шахты лифтом.
В системе отсчёта, связанной с шахтой, груз движется вверх вместе с лифтом с ускорением, равным ускорению лифта . На груз действуют сила тяжести , направленная вертикально вниз, и сила упругости , направленная вертикально вверх. Второй закон Ньютона в данной системе отсчёта выглядит следующим образом:
.
Запишем второй закон Ньютона в проекциях на ось ординат:
.
Динамометр показывает значение, равное модулю силы упругости: . Таким образом, модуль силы упругости превышает модуль силы тяжести на величину, равную .
Примем, что в НИСО силы и , действующие на груз, не изменились. Следовательно, сумма этих сил не равна нулю . Несмотря на это, в системе отсчёта, связанной с лифтом, груз покоится . Получается, что равнодействующая сил и не равна произведению массы тела на ускорение .
Перезапишем уравнение в следующем виде:
.
Обозначим произведение как . Учтём, что ускорение тела в системе отсчёта, связанной с лифтом, равно нулю, тогда выражение выше можно записать в следующем виде:
.
Полученное уравнение называется уравнением движения тела в НИСО.
Векторная величина , равная произведению массы тела m на ускорение НИСО относительно ИСО, взятому со знаком «минус», называется силой инерции: .
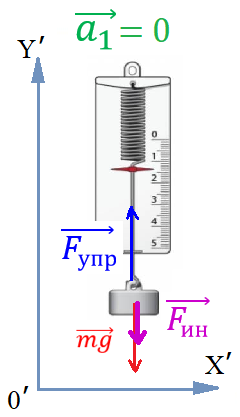 Рис. 3. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением лифте
Рис. 3. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением лифте
Сила инерции направлена в сторону, противоположную направлению ускорения НИСО относительно ИСО (рис. 3). В приведённом примере сила инерции уравновешивает в НИСО действие суммы сил и , благодаря чему в НИСО ускорение груза равно нулю , хотя в ИСО тот же груз движется с ускорением .
Заметим, что невозможно указать тело, со стороны которого действует сила инерции , поэтому не является силой действия одного тела на другое. Использование позволяет записывать уравнение движения тела в НИСО в стандартном виде.
Действие силы инерции в НИСО позволяет объяснять различные физические явления с привычной точки зрения.
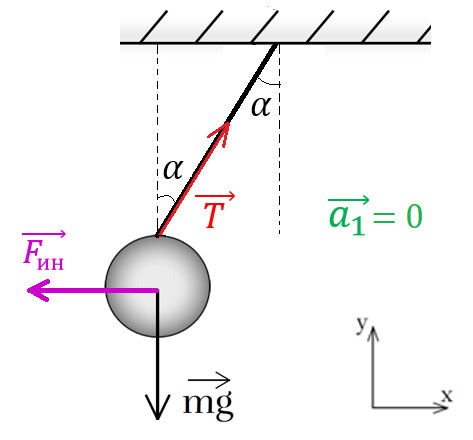 Рис. 4. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением вагоне поезда
Рис. 4. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением вагоне поезда
Например, вспомним задачу, в которой грузик закреплён на нити на потолке вагона (рис. 4). При увеличении скорости вагона относительно Земли — появлении
ускорения — грузик на нити отклонится от вертикали на некоторой угол .
Опишем движение грузика в НИСО, связанной с вагоном.
В НИСО на грузик, помимо прочих, действует сила инерции, направленная горизонтально влево и равная взятому со знаком «−» произведению массы груза m на ускорение вагона в ИСО, связанной с Землёй: .
Именно сила инерции заставляет грузик отклониться от вертикали. Сумма всех сил, действующих на грузик, равна нулю: , поэтому в системе отсчёта, связанной с вагоном, грузик покоится .
Таким образом, в НИСО уравнение движения грузика имеет следующий вид:
.
Заметим, что, если в какой-либо системе отсчёта действует сила инерции, такая система отсчёта является неинерциальной.
Сила прямо пропорциональна массе тела, действие силы инерции аналогично действию гравитационных сил. Так, космонавт, будучи внутри космического корабля, не может определить находится ли его корабль на поверхности Земли или движется с ускорением, равным ускорению свободного падения в космическом пространстве. Благодаря этому силы инерции могут быть использованы для создания «искусственной» гравитации на космических кораблях.
Итоги
- Любая система, которая движется относительно данной инерциальной системы отсчёта равномерно и прямолинейно, является инерциальной.
- Принцип относительности Галилея: при одинаковых начальных условиях все механические процессы протекают одинаково во всех инерциальных системах отсчёта.
- В неинерциальных системах отсчёта (НИСО) тела приобретают ускорение в отсутствие действия на них других тел. В НИСО сумма всех сил , действующих на материальную точку, не равна произведению её массы на ускорение в данной НИСО.
- Векторная величина , равная произведению массы тела на ускорение НИСО относительно ИСО, взятому со знаком «−», называется силой инерции: .
Контрольные вопросы
1. Какие системы отсчёта называются неинерциальными?
2. Сформулируйте принцип относительности Галилея.
3. Дайте определение силы инерции.
- Принцип относительности Галилея. Инерциальные и неинерциальные системы отсчёта
- знать формулировку принципа относительности Галилея; понятия: инерциальная и неинерциальная системы отсчёта, сила инерции
- уметь отличать инерциальные и неинерциальные системы отсчёта; описывать движение тела в неинерциальной системе отсчёта; объяснять физические явления с учётом существования сил инерции
- Сформулируйте закон сложения скоростей.
- Что такое сила инерции?
- Как описать движение тела в неинерциальной системе отсчёта?
Принцип относительности Галилея. Инерциальные и неинерциальные системы отсчёта
В предыдущих параграфах мы описывали характер движения тел относительно лабораторных систем отсчёта, связанных с Землей, то есть относительно инерциальных систем отсчёта. В данном параграфе мы рассмотрим, как описывается характер движения тела в неинерциальных системах отсчёта и выясним, применимы ли законы динамики в этом случае.
Пусть некоторое тело движется как в подвижной системе отсчёта, так и в неподвижной. Относительно ИСО скорость тела постоянна и равна . Относительно подвижной системы отсчёта данное тело движется со скоростью
, скорость подвижной системы отсчёта относительно ИСО равна . Тогда согласно закону сложения скоростей, изученному нами ранее, скорость тела в ИСО . Отсюда получаем, что скорость рассматриваемого тела относительно подвижной системы отсчёта . Из полученной разности следует, что подвижная система отсчёта также будет инерциальной.
Любая система, которая движется относительно данной инерциальной системы отсчёта равномерно и прямолинейно, является инерциальной.
Галилей установил, что характер движения и взаимодействия тел при рассмотрении в различных ИСО не изменяется. Это значит, что равномерное движение относительно Земли не влияет на протекание механических явлений. Представим ситуацию: вы находитесь в вагоне поезда, движущегося равномерно прямолинейно, никаких вибраций и тряски нет. Если в таких условиях подбросить мяч вверх или под углом к горизонту, он будет двигаться точно также, как если проделать эти действия на Земле. Если окна вагона зашторены, невозможно определить, движется ли поезд или находится в состоянии покоя относительно Земли. Результаты подобных экспериментов позволили сформулировать фундаментальный закон природы — принцип относительности Галилея.
Принцип относительности Галилея: при одинаковых начальных условиях все механические процессы протекают одинаково во всех инерциальных системах отсчёта.
 Рис. 1. Движение мячика в ИСО и НИСО
Рис. 1. Движение мячика в ИСО и НИСО
Иначе говоря, законы динамики имеют одинаковый вид во всех ИСО. Следует понимать, что иметь один и тот же вид будут только законы динамики, так как координаты и скорости тел относительно разных систем отсчёта различны, законы движения тел будут отличаться.
Например, находясь в вагоне поезда, движущегося равномерно прямолинейно относительно Земли, отпустим из рук удерживаемый на некоторой высоте мячик.
Вагон представляет собой подвижную систему отсчёта 0’X’Y’ (рис. 1). Относительно вагона проекция скорости мячика на ось 0’X’ в начальный момент времени равна нулю = 0, поэтому в данной системе отсчёта мячик будет свободно падать вертикально вниз.
В то же время относительно неподвижной системы отсчёта 0XY, связанной с Землёй, начальная скорость мячика равна скорости подвижной системы
отсчёта — движущегося вагона поезда. Проекция начальной скорости тела на ось абсцисс в данной системе отсчёта . Траектория движения мячика будет соответствовать траектории тела, брошенного горизонтально, — будет иметь форму параболы.
Таким образом, в приведённом примере законы динамики, описывающие движение мячика, будут иметь одинаковый вид в обеих системах отсчёта, но законы движения будут различны.
Для описания движения тела в подобных случаях используют так называемое преобразование Галилея. Если в рассматриваемой ИСО закон движения материальной точки имеет вид , то в другой ИСО, движущейся поступательно со скоростью относительно данной ИСО, закон движения данной точки выглядит следующим образом:
.
Если в приведённом выше примере поезд приобретёт некоторое ускорение относительно Земли — начнёт разгоняться или тормозить, наблюдатель в вагоне поезда сможет заметить это по изменениям в характере движения окружающих его тел. Так, при торможении поезда тела, находящиеся в вагоне, приобретут ускорение относительно вагона: например, находящиеся на столе предметы придут в движение относительно стола, несмотря на отсутствие действия на них других тел. Следовательно, если движущаяся относительно Земли система отсчёта приобретает ускорение, она перестаёт быть инерциальной и становится неинерциальной.
В неинерциальных системах отсчёта (НИСО) тела приобретают ускорение в отсутствие действия на них других тел.
В НИСО сумма всех сил , действующих на материальную точку, не равна произведению её массы m на ускорение в данной НИСО.
Тот факт, что в НИСО не выполняется равенство , позволяет отличать НИСО от ИСО экспериментально. Например, установлено, что в Южном полушарии нашей планеты у текущих в направлении меридиана рек левый берег выше правого, так как левый берег сильнее подмывается течением. Данное явление получило название закон Бэра в честь учёного, описавшего его в работе под названием «О всеобщем законе образования речных русел». Бэр объяснил асимметрию склонов речных долин вращением Земли вокруг своей оси. Отсюда следует вывод, что лабораторная система отсчёта, связанная с Землёй, является инерциальной лишь приближённо.
Рассмотрим, как записываются уравнения движения в НИСО в случае, если НИСО движется поступательно прямолинейно с ускорением относительно ИСО.
 Рис. 2. Ускорение тела в ИСО и в НИСО
Рис. 2. Ускорение тела в ИСО и в НИСО
Пусть на динамометре висит груз массой m, а динамометр закреплён на потолке лифта. Лифт поднимается в шахте с ускорением (рис. 2).
Опишем движение груза в ИСО, связанной с неподвижной шахтой лифта, и в НИСО, связанной с ускоряющимся относительно шахты лифтом.
В системе отсчёта, связанной с шахтой, груз движется вверх вместе с лифтом с ускорением, равным ускорению лифта . На груз действуют сила тяжести , направленная вертикально вниз, и сила упругости , направленная вертикально вверх. Второй закон Ньютона в данной системе отсчёта выглядит следующим образом:
.
Запишем второй закон Ньютона в проекциях на ось ординат:
.
Динамометр показывает значение, равное модулю силы упругости: . Таким образом, модуль силы упругости превышает модуль силы тяжести на величину, равную .
Примем, что в НИСО силы и , действующие на груз, не изменились. Следовательно, сумма этих сил не равна нулю . Несмотря на это, в системе отсчёта, связанной с лифтом, груз покоится . Получается, что равнодействующая сил и не равна произведению массы тела на ускорение .
Перезапишем уравнение в следующем виде:
.
Обозначим произведение как . Учтём, что ускорение тела в системе отсчёта, связанной с лифтом, равно нулю, тогда выражение выше можно записать в следующем виде:
.
Полученное уравнение называется уравнением движения тела в НИСО.
Векторная величина , равная произведению массы тела m на ускорение НИСО относительно ИСО, взятому со знаком «минус», называется силой инерции: .
 Рис. 3. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением лифте
Рис. 3. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением лифте
Сила инерции направлена в сторону, противоположную направлению ускорения НИСО относительно ИСО (рис. 3). В приведённом примере сила инерции уравновешивает в НИСО действие суммы сил и , благодаря чему в НИСО ускорение груза равно нулю , хотя в ИСО тот же груз движется с ускорением .
Заметим, что невозможно указать тело, со стороны которого действует сила инерции , поэтому не является силой действия одного тела на другое. Использование позволяет записывать уравнение движения тела в НИСО в стандартном виде.
Действие силы инерции в НИСО позволяет объяснять различные физические явления с привычной точки зрения.
 Рис. 4. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением вагоне поезда
Рис. 4. Направление силы инерции, действующей на груз, подвешенный в движущемся с ускорением вагоне поезда
Например, вспомним задачу, в которой грузик закреплён на нити на потолке вагона (рис. 4). При увеличении скорости вагона относительно Земли — появлении
ускорения — грузик на нити отклонится от вертикали на некоторой угол .
Опишем движение грузика в НИСО, связанной с вагоном.
В НИСО на грузик, помимо прочих, действует сила инерции, направленная горизонтально влево и равная взятому со знаком «−» произведению массы груза m на ускорение вагона в ИСО, связанной с Землёй: .
Именно сила инерции заставляет грузик отклониться от вертикали. Сумма всех сил, действующих на грузик, равна нулю: , поэтому в системе отсчёта, связанной с вагоном, грузик покоится .
Таким образом, в НИСО уравнение движения грузика имеет следующий вид:
.
Заметим, что, если в какой-либо системе отсчёта действует сила инерции, такая система отсчёта является неинерциальной.
Сила прямо пропорциональна массе тела, действие силы инерции аналогично действию гравитационных сил. Так, космонавт, будучи внутри космического корабля, не может определить находится ли его корабль на поверхности Земли или движется с ускорением, равным ускорению свободного падения в космическом пространстве. Благодаря этому силы инерции могут быть использованы для создания «искусственной» гравитации на космических кораблях.
Итоги
- Любая система, которая движется относительно данной инерциальной системы отсчёта равномерно и прямолинейно, является инерциальной.
- Принцип относительности Галилея: при одинаковых начальных условиях все механические процессы протекают одинаково во всех инерциальных системах отсчёта.
- В неинерциальных системах отсчёта (НИСО) тела приобретают ускорение в отсутствие действия на них других тел. В НИСО сумма всех сил , действующих на материальную точку, не равна произведению её массы на ускорение в данной НИСО.
- Векторная величина , равная произведению массы тела на ускорение НИСО относительно ИСО, взятому со знаком «−», называется силой инерции: .
Контрольные вопросы
1. Какие системы отсчёта называются неинерциальными?
2. Сформулируйте принцип относительности Галилея.
3. Дайте определение силы инерции.



