Цифровая библиотека

Интернет-библиотека по школьным предметам от «Онлайн-школы». Библиотека поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Например: формулы сокращенного умножения

Выбери класс

Выбери все классы

Все предметы
10 класс
Физика
Динамика равномерного движения материальной точки по окружности

Физика 10 класс Физика 10 класс

Конспект урока: Динамика равномерного движения материальной точки по окружности

Динамика

08.05.2025

3443

Динамика равномерного движения материальной точки по окружности

План урока

Динамика равномерного движения материальной точки по окружности
Примеры решения задач

Цели урока

знать направление и формулу мгновенной скорости при движении по окружности; направление и формулу центростремительного ускорения
уметь находить линейную скорость и центростремительное ускорение тела, движущегося по окружности; применять второй и третий законы Ньютона для решения задач на равномерное движение тела по окружности

Разминка

Как направлена мгновенная скорость тела, движущегося по окружности?
Куда направлена сила трения, действующая на тело, движущееся по окружности?
Как направлена равнодействующая сил тела, движущегося по окружности?

Динамика равномерного движения материальной точки по окружности

Вам уже известно, что материальная точка движется по окружности с постоянной по модулю линейной скоростью $v$ , при этом направление вектора скорости постоянной меняется и в любой момент времени направлено по касательной к окружности, по которой движется тело (рис. 1).

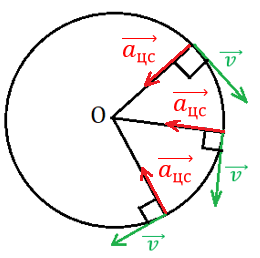Рис. 1. Направление скорости и ускорения тела, движущегося по окружности

Благодаря изменению направления вектора скорости $\vec{v}$ тело, движущееся по окружности, обладает центростремительным ускорением, которое в любой момент времени направлено к центру окружности и вычисляется по следующей формуле:

$a_{цс} = \frac{v^{2}}{R} = ω^{2} \cdot R$ .

По второму закону Ньютона сумма всех сил, действующих на тело, равна произведению массы этого тела на его ускорение: $\vec{F} = m \cdot \vec{a}$ .

Тогда сумма сил, действующих на движущееся по окружности тело, вычисляется по следующей формуле:

$\vec{F} = m \cdot {\vec{a}}_{цс}$ .

В инерциальной системе отсчёта сумма всех сил, действующих на движущееся по окружности тело, равна произведению его массы на центростремительное ускорение: $\vec{F} = m \cdot {\vec{a}}_{цс}$ .

Из соотношения выше следует два важных вывода.

Во-первых, равнодействующая сил, действующих на тело, равномерно движущееся по окружности, в любой момент времени направлена к центру окружности.

Во-вторых, модуль суммы сил может быть рассчитан по следующим формулам:

$F = m \cdot a_{цс} = \frac{m \cdot v^{2}}{R} = m \cdot ω^{2} \cdot R$ .

При решении задач на движение материальной точки по окружности рекомендуется придерживаться следующих правил:

началом отсчёта является центр окружности;
координатную ось проводят через начало отсчёта и точку на окружности, в которой в данный момент находится тело;
положительное направление оси ОХ совпадает с направлением равнодействующей, то есть ось направлена к центру.

Такой выбор системы отсчёта не случаен: проекции центростремительного ускорения и суммы всех сил на ось ОХ в данном случае будут положительны, благодаря чему будет справедливо следующее равенство:

$F = F_{x} = m \cdot a_{цс}$ .

Проекции равнодействующей и ускорения на другие координатные оси в данной системе отсчёта будут равны нулю.

Примеры решения задач

Пример 1

Автомобиль, двигаясь с постоянной скоростью v = 72 км/ч, входит поворот так, что траектория его движения представляет собой дугу окружности радиусом R. При каком минимальном значении радиуса автомобиль не будет соскальзывать с дороги, если коэффициент трения автомобильных шин о дорогу 0,4?

Решение

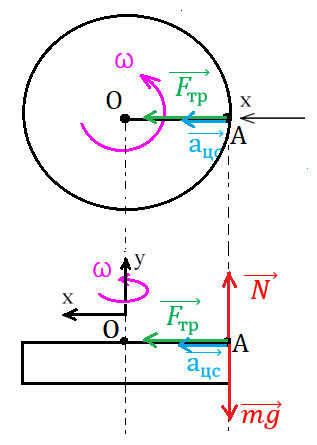Рис. 2. Иллюстрация к примеру 1

1. Автомобиль движется поступательно, следовательно, его можно принять за материальную точку.

2. В качестве тела отсчёта выберем поверхность Земли. Ось ОХ проводим через центр окружности и точку А, в которой в начальный момент находится автомобиль (рис. 2). Координатная ось ОХ направлена к центру окружности. Ось ОY направлена перпендикулярно поверхности Земли.

На тело действует сила трения, направленная к центру вдоль оси ОХ, сила тяжести и сила реакции опоры, действующие вдоль оси OY.

3. Запишем второй закон Ньютона в векторной форме для автомобиля:

${\vec{F}}_{тр} + m \cdot \vec{g} + \vec{N} = m \cdot {\vec{a}}_{цс}$ .

4. Запишем второй закон Ньютона в проекциях на координатные оси:

$OX : F_{тр} = m \cdot a_{цс}$ ;

$OY : N - m \cdot g = 0$ .

5. По условию автомобиль не должен соскальзывать, тогда $F_{т р}$ — это сила трения покоя, поэтому её модуль $F_{тр} \leq μ \cdot N$ .

6. Формула для центростремительного ускорения:

$a_{цс} = \frac{v^{2}}{R}$ .

7. Объединяя пункты выше, получаем систему, состоящую из двух уравнений и одного неравенства:

$\{\begin{matrix} F_{т р} = m \cdot \frac{v^{2}}{R} \\ N - m \cdot g = 0 \\ F_{т р} \leq μ \cdot N \end{matrix}$ .

8. Решая систему, получаем

$m \cdot \frac{v^{2}}{R} \leq μ \cdot m \cdot g$ .

9. Выразим радиус $R$ : $R \geq \frac{v^{2}}{μ g}$ . В задаче просят найти минимальное значение радиуса, тогда в последнем неравенстве следует положить знак «равно»:

$R = \frac{v^{2}}{μ \cdot g} = \frac{20^{2}}{0, 4 \cdot 10} = 100 м$ .

Ответ: $R = 100 м$ .

Пример 2

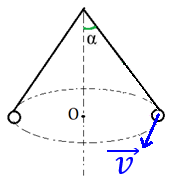Рис. 3. Иллюстрация к примеру 2

Тело, подвешенное на нити, вращается в плоскости, параллельной поверхности Земли (рис. 3). Найти силу натяжения нити и радиус окружности, по которой движется тело, если масса тела m = 200 г, скорость движения $v$ = 4 м/с, а угол $α$ = 30°.

Решение

1. Тело движется поступательно, следовательно, его можно принять за материальную точку.

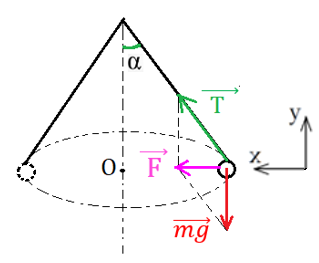Рис. 4. Силы, действующие на тело, вращающееся на нити

2. В качестве тела отсчёта выберем поверхность Земли. Ось ОХ проводим через центр окружности и точку, в которой в начальный момент находится рассматриваемое тело (рис. 4). Координатная ось ОХ направлена к центру окружности, по которой вращается тело. Ось ОY направлена перпендикулярно поверхности Земли.

На тело действует сила натяжения нити и сила тяжести. В данном случае центростремительное ускорение является следствием действия равнодействующей $\vec{F}$ силы тяжести и силы натяжения нити.

3. Запишем второй закон Ньютона в векторной форме:

$m \cdot \vec{g} + \vec{T} = m \cdot {\vec{a}}_{цс}$ .

4. Запишем второй закон Ньютона в проекциях на координатные оси:

$OX : \sin (α) \cdot T = m \cdot a_{цс}$ ;

$OY : \cos (α) \cdot T - m \cdot g = 0$ .

5. Запишем формулу центростремительного ускорения:

$a_{цс} = \frac{v^{2}}{R}$ .

С учётом формулы выше получаем следующую систему уравнений:

$\{\begin{cases} \sin (α) \cdot T = m \cdot \frac{v^{2}}{R} \\ \cos (α) \cdot T = m \cdot g \end{cases}$ .

Из уравнения $\cos (α) \cdot T - m \cdot g = 0$ находим силу натяжения нити:

$T = \frac{m \cdot g}{\cos (α)} = \frac{0, 2 \cdot 10}{\cos (30 °)} \approx 2, 3 Н$ .

Подставляем полученное значение в формулу $\sin (α) \cdot T = m \cdot a_{цс}$ и находим радиус окружности:

$R = \frac{m \cdot v^{2}}{\sin (α) \cdot T} = \frac{0, 2 \cdot 4^{2}}{\sin (30 °) \cdot 2, 3} \approx 2, 8 м$ .

Ответ: $T \approx 2, 3 Н$ ; $R \approx 2, 8 м$ .

Упражнение 1

1. С какой максимальной скоростью может ехать велосипедист по горизонтальной плоскости, описывая дугу радиусом 45 м, если коэффициент трения резины о дорогу 0,5.

2. Автомобиль массой 1,5 т проезжает по выпуклому мосту радиусом 200 м со скоростью 72 км/ч. Найти вес автомобиля в наивысшей точке моста.

Ответы

Упражнение 1

1. $v$ = 15 м/с

2. Р = 12 кН

Динамика равномерного движения материальной точки по окружности

План урока

Динамика равномерного движения материальной точки по окружности
Примеры решения задач

Цели урока

знать направление и формулу мгновенной скорости при движении по окружности; направление и формулу центростремительного ускорения
уметь находить линейную скорость и центростремительное ускорение тела, движущегося по окружности; применять второй и третий законы Ньютона для решения задач на равномерное движение тела по окружности

Разминка

Как направлена мгновенная скорость тела, движущегося по окружности?
Куда направлена сила трения, действующая на тело, движущееся по окружности?
Как направлена равнодействующая сил тела, движущегося по окружности?

Динамика равномерного движения материальной точки по окружности

Рис. 1. Направление скорости и ускорения тела, движущегося по окружности

$a_{цс} = \frac{v^{2}}{R} = ω^{2} \cdot R$ .

Тогда сумма сил, действующих на движущееся по окружности тело, вычисляется по следующей формуле:

$\vec{F} = m \cdot {\vec{a}}_{цс}$ .

Из соотношения выше следует два важных вывода.

Во-вторых, модуль суммы сил может быть рассчитан по следующим формулам:

$F = m \cdot a_{цс} = \frac{m \cdot v^{2}}{R} = m \cdot ω^{2} \cdot R$ .

началом отсчёта является центр окружности;
координатную ось проводят через начало отсчёта и точку на окружности, в которой в данный момент находится тело;
положительное направление оси ОХ совпадает с направлением равнодействующей, то есть ось направлена к центру.

$F = F_{x} = m \cdot a_{цс}$ .

Проекции равнодействующей и ускорения на другие координатные оси в данной системе отсчёта будут равны нулю.

Примеры решения задач

Пример 1

Решение

Рис. 2. Иллюстрация к примеру 1

1. Автомобиль движется поступательно, следовательно, его можно принять за материальную точку.

3. Запишем второй закон Ньютона в векторной форме для автомобиля:

${\vec{F}}_{тр} + m \cdot \vec{g} + \vec{N} = m \cdot {\vec{a}}_{цс}$ .

4. Запишем второй закон Ньютона в проекциях на координатные оси:

$OX : F_{тр} = m \cdot a_{цс}$ ;

$OY : N - m \cdot g = 0$ .

6. Формула для центростремительного ускорения:

$a_{цс} = \frac{v^{2}}{R}$ .

7. Объединяя пункты выше, получаем систему, состоящую из двух уравнений и одного неравенства:

$\{\begin{matrix} F_{т р} = m \cdot \frac{v^{2}}{R} \\ N - m \cdot g = 0 \\ F_{т р} \leq μ \cdot N \end{matrix}$ .

8. Решая систему, получаем

$m \cdot \frac{v^{2}}{R} \leq μ \cdot m \cdot g$ .

$R = \frac{v^{2}}{μ \cdot g} = \frac{20^{2}}{0, 4 \cdot 10} = 100 м$ .

Ответ: $R = 100 м$ .

Пример 2

Рис. 3. Иллюстрация к примеру 2

Решение

1. Тело движется поступательно, следовательно, его можно принять за материальную точку.

Рис. 4. Силы, действующие на тело, вращающееся на нити

3. Запишем второй закон Ньютона в векторной форме:

$m \cdot \vec{g} + \vec{T} = m \cdot {\vec{a}}_{цс}$ .

4. Запишем второй закон Ньютона в проекциях на координатные оси:

$OX : \sin (α) \cdot T = m \cdot a_{цс}$ ;

$OY : \cos (α) \cdot T - m \cdot g = 0$ .

5. Запишем формулу центростремительного ускорения:

$a_{цс} = \frac{v^{2}}{R}$ .

С учётом формулы выше получаем следующую систему уравнений:

$\{\begin{cases} \sin (α) \cdot T = m \cdot \frac{v^{2}}{R} \\ \cos (α) \cdot T = m \cdot g \end{cases}$ .

Из уравнения $\cos (α) \cdot T - m \cdot g = 0$ находим силу натяжения нити:

$T = \frac{m \cdot g}{\cos (α)} = \frac{0, 2 \cdot 10}{\cos (30 °)} \approx 2, 3 Н$ .

Подставляем полученное значение в формулу $\sin (α) \cdot T = m \cdot a_{цс}$ и находим радиус окружности:

$R = \frac{m \cdot v^{2}}{\sin (α) \cdot T} = \frac{0, 2 \cdot 4^{2}}{\sin (30 °) \cdot 2, 3} \approx 2, 8 м$ .

Ответ: $T \approx 2, 3 Н$ ; $R \approx 2, 8 м$ .

Упражнение 1

Ответы

Упражнение 1

1. $v$ = 15 м/с

2. Р = 12 кН

Предыдущий урок

Решение задач о движении взаимодействующих тел

Динамика

Следующий урок

Динамика. Закон инерции. Инерциальные системы отсчета. Первый закон Ньютона. Сила. Измерение сил

Динамика

Урок подготовил(а)

Андрей Михайлович

Учитель физики

Опыт работы: 12 лет

Объектные местоимения

Английский язык
Ориентирование на местности

Окружающий мир
Устройство Римской республики

История

Зарегистрируйся, чтобы присоединиться к обсуждению урока

Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.

Отзывы об уроке:

Пока никто не оставил отзыв об этом уроке