- Третий закон Ньютона. Сила реакции опоры. Вес тела
- знать формулировку третьего закона Ньютона; физический смысл и направление силы реакции опоры и веса тела; понятие «невесомость»
- уметь объяснять, как взаимодействуют два тела; объяснять, при каких условиях вес тела больше или меньше силы тяжести, действующей на тело
- Сформулируйте второй закон Ньютона.
- Почему тела могут покоиться на горизонтальной поверхности, несмотря на действие силы тяжести?
- В каком случае тело находится в состоянии невесомости?
Третий закон Ньютона. Сила реакции опоры. Вес тела
Вам уже известно, что, если одно тело действует на другое с некоторой силой, второе тело также будет действовать на первое с некоторой силой.
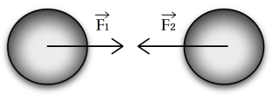 Рис. 1. Взаимное притяжение двух тел
Рис. 1. Взаимное притяжение двух тел
Так, если Земля притягивает к себе тело, расположенное на её поверхности, то и данное тело тоже будет притягивать к себе Землю (рис. 1). Взаимодействие двух тел описывается третьим законом Ньютона.
Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
Отметим, что силы, с которыми взаимодействуют два тела, приложены к разным телам: сила , с которой Земля притягивает человека, приложена к человеку; сила , с которой человек притягивает Землю, — к Земле. В связи с этим силы и не уравновешивают друг друга.
Совместное использование второго и третьего законов Ньютона позволяет решать задачи о движении взаимодействующих тел.
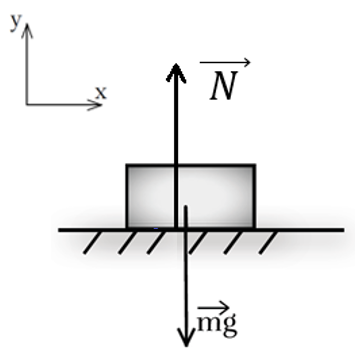 Рис. 2. Силы, действующие на покоящееся относительно поверхности тело
Рис. 2. Силы, действующие на покоящееся относительно поверхности тело
Рассмотрим простой пример. На горизонтальной поверхности, неподвижной относительно Земли, покоится тело массой m (рис. 2). Известно, что на любое тело вблизи поверхности Земли действует сила тяжести .
В ИСО тело находится в состоянии покоя, в этом случае ускорение тела равно нулю. Согласно второму закону Ньютона, равнодействующая сил равна произведению массы на ускорение, следовательно, сумма сил, действующих на данное тело, равна нулю.
Это возможно только в том случае, если сила тяжести уравновешена другой силой, действующей со стороны поверхности на тело, — эта сила называется силой реакции опоры . Запишем второй закон Ньютона для рассматриваемого тела в векторном виде:
.
Учтём, что в рассматриваемом случае ускорение тела равно нулю:
.
 Рис. 3. Направление сил, действующих на тело
Рис. 3. Направление сил, действующих на тело
Это соотношение показывает, что в рассматриваемом случае сила реакции опоры по модулю равна силе тяжести и направлена в противоположную сторону — вертикально вверх. В проекциях на координатную ось второй закон Ньютона будет выглядеть следующим образом:
.
Отметим, что сила реакции опоры не всегда равна силе тяжести, но всегда направлена перпендикулярно поверхности (рис. 3).
Сила реакции опоры — это сила упругости, действующая на тело со стороны опоры перпендикулярно её поверхности.
Если поверхность действует на тело с силой , то тело, согласно третьему закону Ньютона, должно действовать на поверхность с силой, равной по модулю и противоположной по направлению, — эта сила называется весом тела :
.
Вес тела — это сила, с которой тело действует на опору (или подвес), находясь в неподвижном состоянии относительно этой опоры (или подвеса).
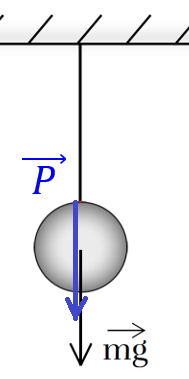 Рис. 4. Направление веса тела
Рис. 4. Направление веса тела
На рисунке 3 показано направление силы тяжести, силы реакции опоры и веса тела в случае, когда тело лежит на наклонной плоскости.
В случае, когда тело находится в состоянии покоя на горизонтальной опоре, вес тела равен силе тяжести . Данное равенство будет справедливо также в случае, когда тело покоится на подвесе (рис. 4).
Вес тела приложен к поверхности, на которой находится тело, сила реакции опоры — к телу, поэтому данные силы приложены к разным телам и не уравновешивают друг друга.
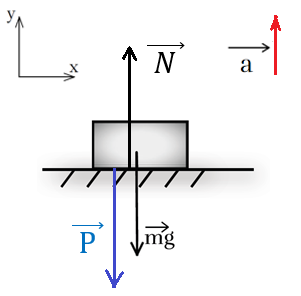 Рис. 5. Движение тела в лифте с ускорением, направленным вверх
Рис. 5. Движение тела в лифте с ускорением, направленным вверх
Рассмотрим другой пример. Пусть на горизонтальном полу лифта лежит ящик массой m. Лифт начинает подниматься на верхний этаж с ускорением (рис. 5).
Второй закон Ньютона в векторной форме для ящика имеет следующий вид:
.
Направим координатные оси так, как показано на рисунке 5, и запишем второй закон Ньютона в проекциях на координатные оси: в данном случае проекции сил и ускорения на ось ОХ равны нулю, поэтому достаточно записать проекцию на ось ординат:
.
Ящик действует на поверхность лифта с силой, равной его весу, поверхность —
с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
С учётом выражения вес ящика при движении лифта вверх будет равен
.
Если тело и опора движутся вместе относительно Земли с ускорением, направленным вверх, то модуль веса тела больше модуля действующей на него силы тяжести.
Такое явление называется перегрузкой. Для количественной оценки перегрузки вводится специальная физическая величина — коэффициент перегрузки, равная отношению модуля веса тела к модулю силы тяжести, действующей на данное тело.
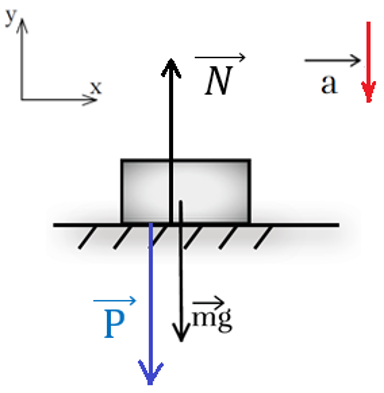 Рис. 6. Движение тела в лифте с ускорением, направленным вниз
Рис. 6. Движение тела в лифте с ускорением, направленным вниз
Рассмотрим обратную ситуацию: тело находится на горизонтальном полу лифта, движущегося вниз с некоторым ускорением (рис. 6).
Второй закон Ньютона в векторной форме для ящика остаётся в прежнем виде:
.
Направим координатные оси так, как показано на рисунке 6, и запишем второй закон Ньютона в проекциях на координатные оси:
.
Ящик действует на поверхность лифта с силой, равной его весу, поверхность —
с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
С учётом выражения вес ящика при движении лифта вниз будет равен
.
Если тело и опора движутся вместе относительно Земли с ускорением, направленным вниз, то модуль веса тела меньше модуля действующей на него силы тяжести.
 a > g тело окажется прижатым к потолку лифта" loading="lazy" />
Рис. 7. При a > g тело окажется прижатым к потолку лифта
a > g тело окажется прижатым к потолку лифта" loading="lazy" />
Рис. 7. При a > g тело окажется прижатым к потолку лифта
В случае, если при движении лифта вниз его ускорение окажется больше ускорения свободного падения, ящик будет прижат к потолку лифта и давить на потолок. Вес тела будет направлен вертикально вверх, а сила реакции опоры — вертикально вниз (рис. 7).
Из уравнения выше следует, что при движении лифта вниз с ускорением, равным по модулю ускорению свободного падения, вес тела, как и сила реакции опоры, окажется равным нулю .
Состояние, при котором вес тела равен нулю , называется невесомостью.
Итоги
- Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
- Сила реакции опоры — это сила упругости, действующая на тело со стороны опоры перпендикулярно её поверхности.
- Вес тела — это сила, с которой тело действует на опору (или подвес), находясь в неподвижном состоянии относительно этой опоры (или подвеса).
- Если тело и опора движутся вместе относительно Земли с ускорением, направленным вверх, то модуль веса тела больше модуля действующей на него силы тяжести. В противном случае, если ускорение лифта направлено вниз, модуль веса тела меньше модуля действующей на него силы тяжести.
- Состояние, при котором вес тела равен нулю , называется невесомостью.
Контрольные вопросы
1. Сформулируйте третий закон Ньютона.
2. В каком случае вес тела больше действующей на него силы тяжести?
3. Почему сила реакции опоры и вес не уравновешивают друг друга?
- Третий закон Ньютона. Сила реакции опоры. Вес тела
- знать формулировку третьего закона Ньютона; физический смысл и направление силы реакции опоры и веса тела; понятие «невесомость»
- уметь объяснять, как взаимодействуют два тела; объяснять, при каких условиях вес тела больше или меньше силы тяжести, действующей на тело
- Сформулируйте второй закон Ньютона.
- Почему тела могут покоиться на горизонтальной поверхности, несмотря на действие силы тяжести?
- В каком случае тело находится в состоянии невесомости?
Третий закон Ньютона. Сила реакции опоры. Вес тела
Вам уже известно, что, если одно тело действует на другое с некоторой силой, второе тело также будет действовать на первое с некоторой силой.
 Рис. 1. Взаимное притяжение двух тел
Рис. 1. Взаимное притяжение двух тел
Так, если Земля притягивает к себе тело, расположенное на её поверхности, то и данное тело тоже будет притягивать к себе Землю (рис. 1). Взаимодействие двух тел описывается третьим законом Ньютона.
Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
Отметим, что силы, с которыми взаимодействуют два тела, приложены к разным телам: сила , с которой Земля притягивает человека, приложена к человеку; сила , с которой человек притягивает Землю, — к Земле. В связи с этим силы и не уравновешивают друг друга.
Совместное использование второго и третьего законов Ньютона позволяет решать задачи о движении взаимодействующих тел.
 Рис. 2. Силы, действующие на покоящееся относительно поверхности тело
Рис. 2. Силы, действующие на покоящееся относительно поверхности тело
Рассмотрим простой пример. На горизонтальной поверхности, неподвижной относительно Земли, покоится тело массой m (рис. 2). Известно, что на любое тело вблизи поверхности Земли действует сила тяжести .
В ИСО тело находится в состоянии покоя, в этом случае ускорение тела равно нулю. Согласно второму закону Ньютона, равнодействующая сил равна произведению массы на ускорение, следовательно, сумма сил, действующих на данное тело, равна нулю.
Это возможно только в том случае, если сила тяжести уравновешена другой силой, действующей со стороны поверхности на тело, — эта сила называется силой реакции опоры . Запишем второй закон Ньютона для рассматриваемого тела в векторном виде:
.
Учтём, что в рассматриваемом случае ускорение тела равно нулю:
.
 Рис. 3. Направление сил, действующих на тело
Рис. 3. Направление сил, действующих на тело
Это соотношение показывает, что в рассматриваемом случае сила реакции опоры по модулю равна силе тяжести и направлена в противоположную сторону — вертикально вверх. В проекциях на координатную ось второй закон Ньютона будет выглядеть следующим образом:
.
Отметим, что сила реакции опоры не всегда равна силе тяжести, но всегда направлена перпендикулярно поверхности (рис. 3).
Сила реакции опоры — это сила упругости, действующая на тело со стороны опоры перпендикулярно её поверхности.
Если поверхность действует на тело с силой , то тело, согласно третьему закону Ньютона, должно действовать на поверхность с силой, равной по модулю и противоположной по направлению, — эта сила называется весом тела :
.
Вес тела — это сила, с которой тело действует на опору (или подвес), находясь в неподвижном состоянии относительно этой опоры (или подвеса).
 Рис. 4. Направление веса тела
Рис. 4. Направление веса тела
На рисунке 3 показано направление силы тяжести, силы реакции опоры и веса тела в случае, когда тело лежит на наклонной плоскости.
В случае, когда тело находится в состоянии покоя на горизонтальной опоре, вес тела равен силе тяжести . Данное равенство будет справедливо также в случае, когда тело покоится на подвесе (рис. 4).
Вес тела приложен к поверхности, на которой находится тело, сила реакции опоры — к телу, поэтому данные силы приложены к разным телам и не уравновешивают друг друга.
 Рис. 5. Движение тела в лифте с ускорением, направленным вверх
Рис. 5. Движение тела в лифте с ускорением, направленным вверх
Рассмотрим другой пример. Пусть на горизонтальном полу лифта лежит ящик массой m. Лифт начинает подниматься на верхний этаж с ускорением (рис. 5).
Второй закон Ньютона в векторной форме для ящика имеет следующий вид:
.
Направим координатные оси так, как показано на рисунке 5, и запишем второй закон Ньютона в проекциях на координатные оси: в данном случае проекции сил и ускорения на ось ОХ равны нулю, поэтому достаточно записать проекцию на ось ординат:
.
Ящик действует на поверхность лифта с силой, равной его весу, поверхность —
с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
С учётом выражения вес ящика при движении лифта вверх будет равен
.
Если тело и опора движутся вместе относительно Земли с ускорением, направленным вверх, то модуль веса тела больше модуля действующей на него силы тяжести.
Такое явление называется перегрузкой. Для количественной оценки перегрузки вводится специальная физическая величина — коэффициент перегрузки, равная отношению модуля веса тела к модулю силы тяжести, действующей на данное тело.
 Рис. 6. Движение тела в лифте с ускорением, направленным вниз
Рис. 6. Движение тела в лифте с ускорением, направленным вниз
Рассмотрим обратную ситуацию: тело находится на горизонтальном полу лифта, движущегося вниз с некоторым ускорением (рис. 6).
Второй закон Ньютона в векторной форме для ящика остаётся в прежнем виде:
.
Направим координатные оси так, как показано на рисунке 6, и запишем второй закон Ньютона в проекциях на координатные оси:
.
Ящик действует на поверхность лифта с силой, равной его весу, поверхность —
с силой реакции опоры. По третьему закону Ньютона эти силы равны по модулю и противоположны по направлению:
.
С учётом выражения вес ящика при движении лифта вниз будет равен
.
Если тело и опора движутся вместе относительно Земли с ускорением, направленным вниз, то модуль веса тела меньше модуля действующей на него силы тяжести.
 a > g тело окажется прижатым к потолку лифта" loading="lazy" />
Рис. 7. При a > g тело окажется прижатым к потолку лифта
a > g тело окажется прижатым к потолку лифта" loading="lazy" />
Рис. 7. При a > g тело окажется прижатым к потолку лифта
В случае, если при движении лифта вниз его ускорение окажется больше ускорения свободного падения, ящик будет прижат к потолку лифта и давить на потолок. Вес тела будет направлен вертикально вверх, а сила реакции опоры — вертикально вниз (рис. 7).
Из уравнения выше следует, что при движении лифта вниз с ускорением, равным по модулю ускорению свободного падения, вес тела, как и сила реакции опоры, окажется равным нулю .
Состояние, при котором вес тела равен нулю , называется невесомостью.
Итоги
- Третий закон Ньютона: в инерциальной системе отсчёта два тела взаимодействуют с силами и , равными по модулю, противоположными по направлению и лежащими вдоль одной прямой: .
- Сила реакции опоры — это сила упругости, действующая на тело со стороны опоры перпендикулярно её поверхности.
- Вес тела — это сила, с которой тело действует на опору (или подвес), находясь в неподвижном состоянии относительно этой опоры (или подвеса).
- Если тело и опора движутся вместе относительно Земли с ускорением, направленным вверх, то модуль веса тела больше модуля действующей на него силы тяжести. В противном случае, если ускорение лифта направлено вниз, модуль веса тела меньше модуля действующей на него силы тяжести.
- Состояние, при котором вес тела равен нулю , называется невесомостью.
Контрольные вопросы
1. Сформулируйте третий закон Ньютона.
2. В каком случае вес тела больше действующей на него силы тяжести?
3. Почему сила реакции опоры и вес не уравновешивают друг друга?



