- Наклонная плоскость
- Рычаг
- Блок
- Коэффициент полезного действия
- знать, для чего и как используется наклонная плоскость
- знать, для чего и как используется рычаг
- знать, для чего и как используется блок
- уметь находить коэффициент полезного действия
- Что такое механическая работа?
- Чему равна сила трения?
- Чему равен момент силы?
Наклонная плоскость
Ещё из древних времён известно, что основными помощниками человека являлись простые механизмы, например, наклонная плоскость, рычаги, блоки, колёса, шестерёнки. Главной задачей простых механизмов является упрощение процесса выполняемой работы.
Простые механизмы — приспособления, служащие для преобразования силы.
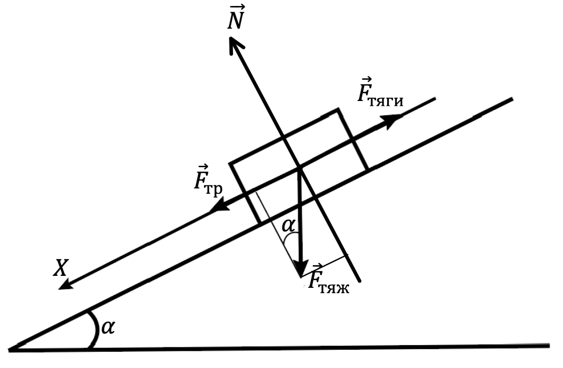 Рис. 1. Наклонная плоскость
Рис. 1. Наклонная плоскость
В Древнем Египте было распространено использование наклонной плоскости, которая применялась для того, чтобы тела большой массы можно было перемещать на высоту под действием силы, значительно меньшей веса тела, тем самым получая выигрыш в силе. Давайте определим, какой выигрыш в силе даёт наклонная плоскость. Рассмотрим рисунок 1 и найдём, какую силу надо приложить к телу, чтобы двигаться вверх по наклонной плоскости. В проекциях на ось OX, направленную вдоль наклонной плоскости:
.
Если силами трения можно пренебречь, то отношение модуля силы , обеспечивающей движение тела по наклонной плоскости, к модулю силы тяжести равно
.
Мы получили, что при отсутствии трения применение наклонной плоскости позволяет уменьшить значение силы, необходимой для перемещения тела по наклонной плоскости, во столько раз, во сколько высота наклонной плоскости меньше её длины .
Заметим, что выигрыша в работе наклонная плоскость не даёт, так как путь увеличивается во столько раз, во сколько уменьшается модуль действующей силы:
.
Такая же работа совершается при вертикальном подъёме тела на высоту. Этот результат является следствием закона сохранения механической энергии, так как работа силы тяжести не зависит от формы пути и равна изменению потенциальной энергии.
Рычаг
Рычаг используется для подъёма тяжёлых предметов, а также является элементом многих современных орудий труда: ножниц, плоскогубцев, ручного тормоза, стрел подъёмного крана. Рычаг находится в равновесии, если момент сил, вращающих его в направлении по часовой стрелке, равен по модулю моменту сил, вращающих его против часовой стрелки.
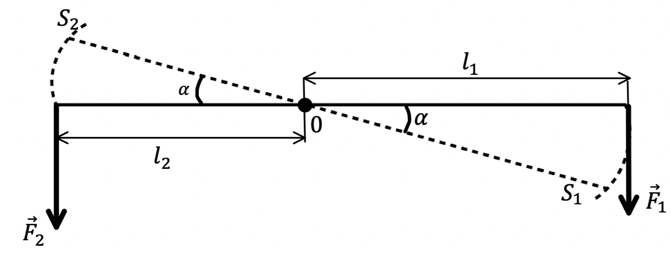 Рис. 2. Рычаг
Рис. 2. Рычаг
Если направления векторов и перпендикулярны кратчайшим прямым, соединяющим точки приложения сил и ось вращения, и лежат в одной плоскости, то условие равенства моментов принимает следующий вид:
,
где и — расстояния от точек приложения сил до точки опоры рычага, то есть оси вращения (см. рис. 2). Если , то рычаг может дать выигрыш в силе в раз:
.
Получение с помощью рычага выигрыша в силе не означает выигрыша в работе. При повороте рычага вокруг точки опоры на угол сила совершает работу
,
сила совершает работу
.
Так как , то работа , совершённая силой , равна работе , соверш`нной силой :
.
Равенство работ и есть следствие закона сохранения механической энергии. Во сколько раз рычаг даёт выигрыш в силе, во столько раз даёт проигрыш в расстоянии.
Блок
Принято различать два вида блоков: подвижный и неподвижный. Небольшое колесо, закреплённое на неподвижной оси, используется в качестве неподвижного блока. Неподвижный блок позволяет только изменять направление действия силы. Плечи сил, приложенных к разным точкам неподвижного блока (точки A и B), одинаковы, поэтому неподвижный блок не даёт выигрыша в силе (рис. 3, а).
 Рис. 3. Блок: a) неподвижный; b) подвижный
Рис. 3. Блок: a) неподвижный; b) подвижный
При подъёме груза массой с помощью подвижного блока получается выигрыш в силе в два раза, так как плечо OA силы в два раза меньше плеча OB силы натяжения троса (рис. 3, b). Заметим, что при вытягивании троса или верёвки на длину груз поднимается лишь на высоту ; следовательно, и подвижный блок не даёт выигрыша в работе.
Неподвижный блок изменяет направление действия силы и является рычагом с равными плечами.
и
При этом нет выигрыша в силе.
Подвижный блок не изменяет направления действия силы и является рычагом с соотношением . Следовательно, такой блок даёт выигрыш в силе:
,
но при этом получаем проигрыш в перемещении!
Рассмотрение простых механизмов показало, что, выигрывая в силе, мы сразу же проигрываем в перемещении, тем самым выигрыша в работе мы не получаем. Таким образом, можно сформулировать одно из основных правил механики, которое именуется «золотым».
Золотое правило механики
Простые механизмы не дают выигрыша в работе: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
Коэффициент полезного действия
Каждый вид энергии может превратиться полностью в любой другой вид энергии. Однако не так всё радужно, как кажется, так как для всех реальных энергетических машин имеет место потеря энергии. Основной источник потерь энергии всем хорошо известен — это трение. Чем меньше общих потерь энергии, тем совершеннее получается машина. Степень совершенства машины характеризуется коэффициентом полезного действия (КПД).
Коэффициентом полезного действия машины называется отношение полезно используемой энергии к энергии , подводимой к данной машине:
.
Для определения КПД справедливы альтернативные формулы:
,
где — полезная работа, — вся затраченная работа.
,
где — полезная мощность, — вся затраченная мощность.
Пример 1
Найти КПД наклонной плоскости длиной 12 м и высотой 5 м, если коэффициент трения при равномерном движении по ней тела равен 0,33.
Решение
1. Запишем исходные данные:
.
2. Сделаем схематический рисунок с указанием всех сил и применим второй закон Ньютона.
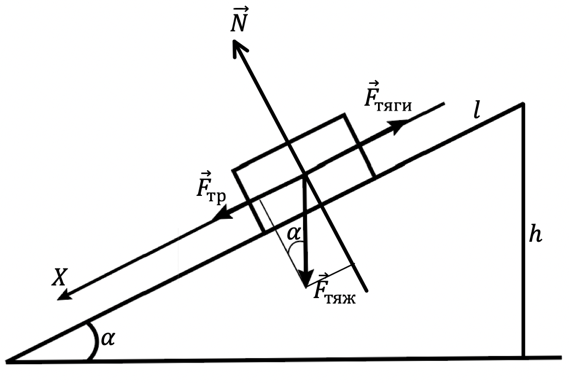
.
Спроецируем на оси:
;
;
.
Так как угол нам неизвестен, выразим его через длину и высоту, используя теорему Пифагора:
,
.
3. Полезной работой в данной задаче мы назовём приращение потенциальной энергии. То есть основной задачей является подъём тела на высоту , но, помимо этого, мы затратим дополнительную работу против сил трения
.
Полная работа совершается силой тяги:
.
4. Найдём КПД:
;
.
Ответ: .
Упражнение 1
1. Какую наименьшую работу надо совершить, чтобы по плоскости с углом наклона 30° на высоту 2 м втащить груз, прикладывая силу, совпадающую по направлению с перемещением? Масса груза 400 кг, коэффициент трения 0,3. Каков при этом КПД?
Контрольные вопросы
1. Даёт ли наклонная плоскость выигрыш в силе? А в работе?
2. Какой выигрыш в силе даёт рычаг?
3. Почему неподвижный блок не даёт выигрыша в силе?
4. Даёт ли выигрыш в работе блок, рычаг?
5. Что такое коэффициент полезного действия и как его найти?
Упражнение 1
1. 12 кДж; 66 %
- Наклонная плоскость
- Рычаг
- Блок
- Коэффициент полезного действия
- знать, для чего и как используется наклонная плоскость
- знать, для чего и как используется рычаг
- знать, для чего и как используется блок
- уметь находить коэффициент полезного действия
- Что такое механическая работа?
- Чему равна сила трения?
- Чему равен момент силы?
Наклонная плоскость
Ещё из древних времён известно, что основными помощниками человека являлись простые механизмы, например, наклонная плоскость, рычаги, блоки, колёса, шестерёнки. Главной задачей простых механизмов является упрощение процесса выполняемой работы.
Простые механизмы — приспособления, служащие для преобразования силы.
 Рис. 1. Наклонная плоскость
Рис. 1. Наклонная плоскость
В Древнем Египте было распространено использование наклонной плоскости, которая применялась для того, чтобы тела большой массы можно было перемещать на высоту под действием силы, значительно меньшей веса тела, тем самым получая выигрыш в силе. Давайте определим, какой выигрыш в силе даёт наклонная плоскость. Рассмотрим рисунок 1 и найдём, какую силу надо приложить к телу, чтобы двигаться вверх по наклонной плоскости. В проекциях на ось OX, направленную вдоль наклонной плоскости:
.
Если силами трения можно пренебречь, то отношение модуля силы , обеспечивающей движение тела по наклонной плоскости, к модулю силы тяжести равно
.
Мы получили, что при отсутствии трения применение наклонной плоскости позволяет уменьшить значение силы, необходимой для перемещения тела по наклонной плоскости, во столько раз, во сколько высота наклонной плоскости меньше её длины .
Заметим, что выигрыша в работе наклонная плоскость не даёт, так как путь увеличивается во столько раз, во сколько уменьшается модуль действующей силы:
.
Такая же работа совершается при вертикальном подъёме тела на высоту. Этот результат является следствием закона сохранения механической энергии, так как работа силы тяжести не зависит от формы пути и равна изменению потенциальной энергии.
Рычаг
Рычаг используется для подъёма тяжёлых предметов, а также является элементом многих современных орудий труда: ножниц, плоскогубцев, ручного тормоза, стрел подъёмного крана. Рычаг находится в равновесии, если момент сил, вращающих его в направлении по часовой стрелке, равен по модулю моменту сил, вращающих его против часовой стрелки.
 Рис. 2. Рычаг
Рис. 2. Рычаг
Если направления векторов и перпендикулярны кратчайшим прямым, соединяющим точки приложения сил и ось вращения, и лежат в одной плоскости, то условие равенства моментов принимает следующий вид:
,
где и — расстояния от точек приложения сил до точки опоры рычага, то есть оси вращения (см. рис. 2). Если , то рычаг может дать выигрыш в силе в раз:
.
Получение с помощью рычага выигрыша в силе не означает выигрыша в работе. При повороте рычага вокруг точки опоры на угол сила совершает работу
,
сила совершает работу
.
Так как , то работа , совершённая силой , равна работе , соверш`нной силой :
.
Равенство работ и есть следствие закона сохранения механической энергии. Во сколько раз рычаг даёт выигрыш в силе, во столько раз даёт проигрыш в расстоянии.
Блок
Принято различать два вида блоков: подвижный и неподвижный. Небольшое колесо, закреплённое на неподвижной оси, используется в качестве неподвижного блока. Неподвижный блок позволяет только изменять направление действия силы. Плечи сил, приложенных к разным точкам неподвижного блока (точки A и B), одинаковы, поэтому неподвижный блок не даёт выигрыша в силе (рис. 3, а).
 Рис. 3. Блок: a) неподвижный; b) подвижный
Рис. 3. Блок: a) неподвижный; b) подвижный
При подъёме груза массой с помощью подвижного блока получается выигрыш в силе в два раза, так как плечо OA силы в два раза меньше плеча OB силы натяжения троса (рис. 3, b). Заметим, что при вытягивании троса или верёвки на длину груз поднимается лишь на высоту ; следовательно, и подвижный блок не даёт выигрыша в работе.
Неподвижный блок изменяет направление действия силы и является рычагом с равными плечами.
и
При этом нет выигрыша в силе.
Подвижный блок не изменяет направления действия силы и является рычагом с соотношением . Следовательно, такой блок даёт выигрыш в силе:
,
но при этом получаем проигрыш в перемещении!
Рассмотрение простых механизмов показало, что, выигрывая в силе, мы сразу же проигрываем в перемещении, тем самым выигрыша в работе мы не получаем. Таким образом, можно сформулировать одно из основных правил механики, которое именуется «золотым».
Золотое правило механики
Простые механизмы не дают выигрыша в работе: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
Коэффициент полезного действия
Каждый вид энергии может превратиться полностью в любой другой вид энергии. Однако не так всё радужно, как кажется, так как для всех реальных энергетических машин имеет место потеря энергии. Основной источник потерь энергии всем хорошо известен — это трение. Чем меньше общих потерь энергии, тем совершеннее получается машина. Степень совершенства машины характеризуется коэффициентом полезного действия (КПД).
Коэффициентом полезного действия машины называется отношение полезно используемой энергии к энергии , подводимой к данной машине:
.
Для определения КПД справедливы альтернативные формулы:
,
где — полезная работа, — вся затраченная работа.
,
где — полезная мощность, — вся затраченная мощность.
Пример 1
Найти КПД наклонной плоскости длиной 12 м и высотой 5 м, если коэффициент трения при равномерном движении по ней тела равен 0,33.
Решение
1. Запишем исходные данные:
.
2. Сделаем схематический рисунок с указанием всех сил и применим второй закон Ньютона.

.
Спроецируем на оси:
;
;
.
Так как угол нам неизвестен, выразим его через длину и высоту, используя теорему Пифагора:
,
.
3. Полезной работой в данной задаче мы назовём приращение потенциальной энергии. То есть основной задачей является подъём тела на высоту , но, помимо этого, мы затратим дополнительную работу против сил трения
.
Полная работа совершается силой тяги:
.
4. Найдём КПД:
;
.
Ответ: .
Упражнение 1
1. Какую наименьшую работу надо совершить, чтобы по плоскости с углом наклона 30° на высоту 2 м втащить груз, прикладывая силу, совпадающую по направлению с перемещением? Масса груза 400 кг, коэффициент трения 0,3. Каков при этом КПД?
Контрольные вопросы
1. Даёт ли наклонная плоскость выигрыш в силе? А в работе?
2. Какой выигрыш в силе даёт рычаг?
3. Почему неподвижный блок не даёт выигрыша в силе?
4. Даёт ли выигрыш в работе блок, рычаг?
5. Что такое коэффициент полезного действия и как его найти?
Упражнение 1
1. 12 кДж; 66 %



