- Определение потенциальной энергии
- Потенциальная энергия взаимодействия тела с Землёй. Работа силы тяжести
- Потенциальная энергия деформированной пружины
- знать формулы для расчёта потенциальной энергии взаимодействия тела с Землёй и потенциальной энергии упруго деформированной пружины; связь между работой внутренних сил и изменением потенциальной энергии тела
- уметь выводить формулы для расчёта потенциальной энергии взаимодействия тела с Землей и потенциальной энергии упруго деформированной пружины
- По какой формуле рассчитывается работа силы?
- Как связаны работа и кинетическая энергия тела?
- Какие тела обладают потенциальной энергией?
Определение потенциальной энергии
Из курса физики 7 класса вам уже известно, что пружина, растянутая (или сжатая) на величину , способна совершить работу, равную: , а тело, поднятое над Землёй на высоту h, работу .
В обоих случаях при совершении работы изменяется потенциальная энергия тел, участвующих во взаимодействии.
Потенциальная энергия тела Eпот — это энергия взаимодействия системы тел или частей одного тела друг с другом.
Потенциальной энергией обладают пружина в деформированном состоянии (растянутая или сжатая), тело, поднятое над Землёй на некоторую высоту и заряженные тела.
Потенциальная энергия системы тел равна работе, которую совершают потенциальные силы взаимодействия её тел при переходе системы из данного состояния в состояние, потенциальная энергия которого равна нулю.
Потенциальная энергия взаимодействия тела с Землёй. Работа силы тяжести
Пусть тело массой m находится на некоторой высоте h над поверхностью Земли, потенциальная энергия рассматриваемого тела на данной высоте равна .
Потенциальная энергия тела в поле тяжести Земли вычисляется по формуле .
На поверхности Земли, где h = 0, потенциальная энергия взаимодействия тела и Земли равна нулю Eпот = 0.
Тогда при падении тела с высоты h на Землю силой тяжести будет совершена работа, численно равная начальной потенциальной энергии тела:
.
Рассмотрим другой пример. Пусть тело перемещается из точки А в точку В, направление вектора перемещения тела составляет угол с вектором силы тяжести (рис. 1). В начальный момент времени тело находится на высоте h0, в конце рассматриваемого промежутка времени — на высоте h.
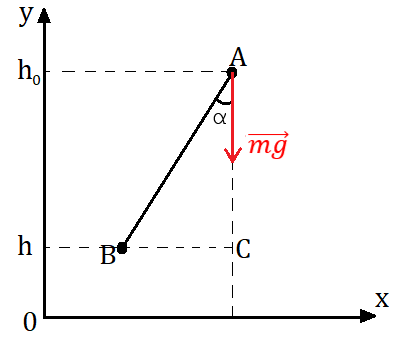 Рис. 1. Расчёт работы силы тяжести при перемещении тела по прямолинейной траектории
Рис. 1. Расчёт работы силы тяжести при перемещении тела по прямолинейной траектории
Тогда начальная и конечная потенциальные энергии тела равны соответственно
и .
В этом случае работа силы тяжести по перемещению тела из точки А в точку В равна:
.
Учтём, что произведение , тогда справедлива следующая запись:
.
Это выражение говорит о том, что работа силы тяжести зависит только от начальной и конечной координаты тела и не зависит от траектории движения тела. Чтобы подтвердить данное утверждение, рассмотрим ещё один пример.
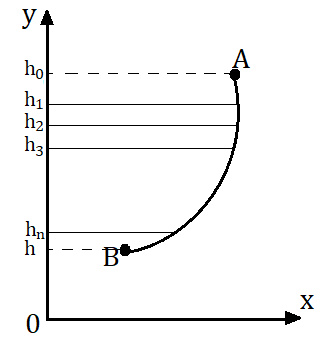 Рис. 2. Расчёт работы силы тяжести при перемещении тела по криволинейной траектории
Рис. 2. Расчёт работы силы тяжести при перемещении тела по криволинейной траектории
Пусть материальная точка движется по криволинейной траектории АВ (рис. 2). Чтобы найти работу силы тяжести в данном случае, необходимо разбить траекторию движения на достаточно малые промежутки, такие, что движение на них можно будет считать прямолинейным. Тогда работа силы тяжести по перемещению тела из точки А в точку В будет равна сумме работ на достаточно малых участках траектории:
.
Если раскрыть скобки и привести подобные, работа силы тяжести окажется равной разности потенциальных энергий:
.
Работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
Потенциальными или консервативными являются те силы, работа которых не зависит от формы траектории данного тела, а определяется лишь начальным и конечным положениями. Сила тяжести, сила упругости и электростатические силы являются примерами потенциальных сил.
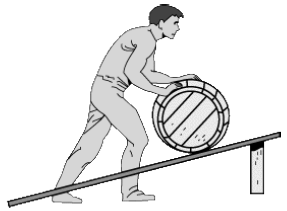 Рис. 3. Наклонная плоскость
Рис. 3. Наклонная плоскость
Вспомним один из знакомых нам простых
механизмов — наклонную плоскость (рис. 3). Наклонная плоскость даёт выигрыш в силе: при подъёме груза вдоль наклонной плоскости требуется меньшая сила, чем если поднимать данное тело вертикально, однако модуль перемещения в первом случае будет больше. Таким образом, наклонная плоскость не даёт выигрыша в работе: как при подъёме вдоль наклонной плоскости, так и при вертикальном подъёме будет совершена одинаковая работа, равная изменению потенциальной энергии груза.
Отметим, что, согласно теореме о кинетической энергии, работа равна разности конечной и начальной кинетической энергии:
.
В случае изменения потенциальной энергии работа равна разности начальной и конечной потенциальной энергии тела:
или .
Работа внутренних сил системы равна изменению потенциальной энергии системы, взятому со знаком «−»: .
Из формулы выше следует, что если потенциальная энергия системы возрастает Eпот > Eпот0, работа внутренних сил системы имеет отрицательное значение. Например, тело поднимают на некоторую высоту: потенциальная энергия камня увеличивается, сила тяжести совершает отрицательную работу.
Чтобы поднять камень, необходимо приложить некоторую силу. Таким образом, на камень действуют внешние силы, направление которых совпадает с направлением перемещения камня — внешние силы совершают положительную работу.
Потенциальная энергия деформированной пружины
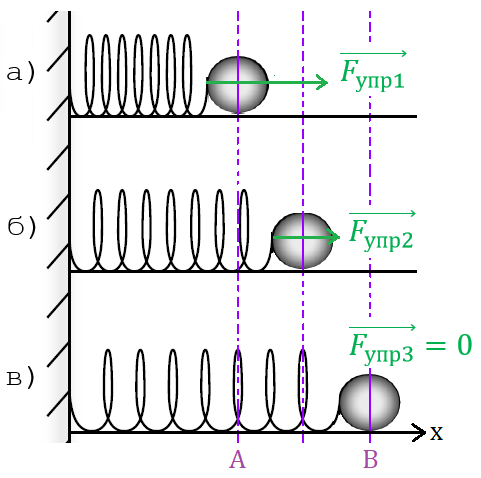 Рис. 4. Сила упругости совершает положительную работу
Рис. 4. Сила упругости совершает положительную работу
Пусть пружину жёсткостью k сжали на величину (рис. 4). Тогда на шарик, прикреплённый к пружине, действует сила , равная по модулю .
Под действием силы упругости пружина вернётся в недеформированное состояние — точку В. Сила упругости при этом совершит работу А. Пусть начальная потенциальная энергия Eпот0, конечная — Eпот. Тогда работа силы упругости равна
.
Потенциальная энергия недеформированной пружины равна нулю Eпот = 0, тогда работа силы упругости равна
.
Сила упругости, возникающая в пружине, прямо пропорциональна величине , следовательно, по мере движения шарика от точки А к точке В модуль силы упругости будет уменьшаться пропорционально её деформации от максимального значения вплоть до нуля .
На рисунке 5 показана зависимость модуля силы упругости от величины деформации пружины.
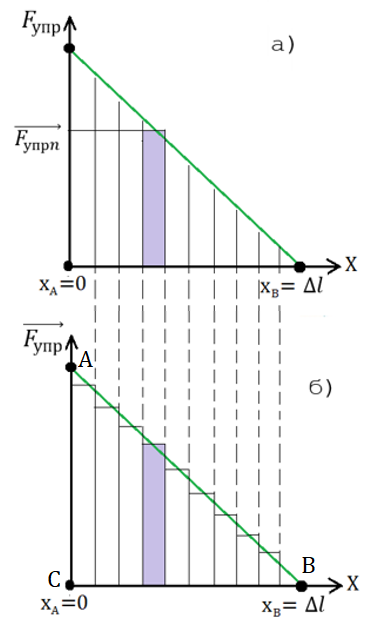 Рис. 5. Зависимость модуля силы упругости от величины деформации пружины
Рис. 5. Зависимость модуля силы упругости от величины деформации пружины
Нам уже известно, что, если сила, действующая на тело, изменяется с течением времени, для вычисления работы такой силы перемещение необходимо разбить на достаточно малые промежутки времени, на каждом из которых силу можно считать величиной постоянной.
Пусть отрезок АВ представляет собой совокупность достаточно малых отрезков Δх0, Δх1, Δх2 … и т. д. (рис. 5, а). Тогда модуль силы упругости Fупрn на отрезке от хn до хn + Δxn можно считать неизменным во времени.
Работа силы упругости на рассматриваемом участке равна . Из рисунка видно, что работа равна площади заштрихованного прямоугольника .
Очевидно, что на каждом достаточно малом участке работа силы упругости будет равна площади соответствующего прямоугольника (рис. 5, б).
Общая работа равна сумме работ на достаточно малых промежутках, следовательно, общая работа равна сумме площадей полученных прямоугольников A = S1 + S2 + … + Sn. Чем больше вводится элементарных отрезков, тем точнее будет вычислена работа силы упругости. При разбиении на достаточно малые промежутки отрезка АВ сумма площадей всех прямоугольников будет приблизительно равна площади прямоугольного треугольника АВС:
.
Учитывая соотношение, получаем, что потенциальная энергия деформированной пружины равна
,
где Eпот0 [Дж] — потенциальная энергия деформированной пружины;
k [Н/м] — жёсткость пружины;
[м] — величина деформации (удлинение пружины).
Потенциальная энергия деформированной пружины вычисляется по формуле .
Пример 1
Камень массой 5 кг свободно падает вертикально вниз с высоты
см. Определите, какую работу совершила сила тяжести к моменту времени, когда камень находился на высоте см.
Решение
 Рис. 6. К примеру 1
Рис. 6. К примеру 1
1. Сделаем схематический рисунок, при этом примем рассматриваемое тело за материальную точку. Систему отсчёта свяжем с поверхностью Земли.
2. Запишем выражение для работы силы тяжести:
.
3. Подставляя исходные данные задачи в формулу для расчёта работы, получим окончательный ответ:
Дж.
4. Заметим, что тот же результат можно было получить, используя общее определение механической работы. Сила, совершающая работу, направлена вертикально вниз, туда же направлено и перемещение тела, тогда
Дж.
Ответ: А=7 Дж.
Итоги
- Потенциальная энергия тела — это энергия взаимодействия системы тел или частей одного тела друг с другом.
- Потенциальная энергия системы тел равна работе, которую совершают потенциальные силы взаимодействия её тел при переходе системы из данного состояния в состояние, потенциальная энергия которого равна нулю.
- Потенциальная энергия тела в поле тяжести Земли вычисляется по формуле .
- Работа внутренних сил системы равна изменению потенциальной энергии системы, взятому со знаком «−»: .
- Потенциальная энергия деформированной пружины вычисляется по формуле .
Упражнение 1
1. Определите потенциальную энергию:
а) тела массой 1,8 кг, поднятого над землёй на высоту 7 м;
б) деформированной пружины жёсткостью 600 Н/м, растянутой на 24 см от положения равновесия.
2. Пружину сжали на см от положения равновесия и отпустили. Какую работу совершила сила упругости к моменту времени, когда смещение от положения равновесия составляло см? Жёсткость пружины равна 400 Н/м.
Контрольные вопросы
1. В чём физический смысл потенциальной энергии?
2. Как связаны работа внутренних сил и потенциальная энергия тела?
3. По какой формуле вычисляется потенциальная энергия упруго деформированной пружины?
Упражнение 1
1. а) 126 Дж; б) 17,28 Дж
2. 4 Дж
- Определение потенциальной энергии
- Потенциальная энергия взаимодействия тела с Землёй. Работа силы тяжести
- Потенциальная энергия деформированной пружины
- знать формулы для расчёта потенциальной энергии взаимодействия тела с Землёй и потенциальной энергии упруго деформированной пружины; связь между работой внутренних сил и изменением потенциальной энергии тела
- уметь выводить формулы для расчёта потенциальной энергии взаимодействия тела с Землей и потенциальной энергии упруго деформированной пружины
- По какой формуле рассчитывается работа силы?
- Как связаны работа и кинетическая энергия тела?
- Какие тела обладают потенциальной энергией?
Определение потенциальной энергии
Из курса физики 7 класса вам уже известно, что пружина, растянутая (или сжатая) на величину , способна совершить работу, равную: , а тело, поднятое над Землёй на высоту h, работу .
В обоих случаях при совершении работы изменяется потенциальная энергия тел, участвующих во взаимодействии.
Потенциальная энергия тела Eпот — это энергия взаимодействия системы тел или частей одного тела друг с другом.
Потенциальной энергией обладают пружина в деформированном состоянии (растянутая или сжатая), тело, поднятое над Землёй на некоторую высоту и заряженные тела.
Потенциальная энергия системы тел равна работе, которую совершают потенциальные силы взаимодействия её тел при переходе системы из данного состояния в состояние, потенциальная энергия которого равна нулю.
Потенциальная энергия взаимодействия тела с Землёй. Работа силы тяжести
Пусть тело массой m находится на некоторой высоте h над поверхностью Земли, потенциальная энергия рассматриваемого тела на данной высоте равна .
Потенциальная энергия тела в поле тяжести Земли вычисляется по формуле .
На поверхности Земли, где h = 0, потенциальная энергия взаимодействия тела и Земли равна нулю Eпот = 0.
Тогда при падении тела с высоты h на Землю силой тяжести будет совершена работа, численно равная начальной потенциальной энергии тела:
.
Рассмотрим другой пример. Пусть тело перемещается из точки А в точку В, направление вектора перемещения тела составляет угол с вектором силы тяжести (рис. 1). В начальный момент времени тело находится на высоте h0, в конце рассматриваемого промежутка времени — на высоте h.
 Рис. 1. Расчёт работы силы тяжести при перемещении тела по прямолинейной траектории
Рис. 1. Расчёт работы силы тяжести при перемещении тела по прямолинейной траектории
Тогда начальная и конечная потенциальные энергии тела равны соответственно
и .
В этом случае работа силы тяжести по перемещению тела из точки А в точку В равна:
.
Учтём, что произведение , тогда справедлива следующая запись:
.
Это выражение говорит о том, что работа силы тяжести зависит только от начальной и конечной координаты тела и не зависит от траектории движения тела. Чтобы подтвердить данное утверждение, рассмотрим ещё один пример.
 Рис. 2. Расчёт работы силы тяжести при перемещении тела по криволинейной траектории
Рис. 2. Расчёт работы силы тяжести при перемещении тела по криволинейной траектории
Пусть материальная точка движется по криволинейной траектории АВ (рис. 2). Чтобы найти работу силы тяжести в данном случае, необходимо разбить траекторию движения на достаточно малые промежутки, такие, что движение на них можно будет считать прямолинейным. Тогда работа силы тяжести по перемещению тела из точки А в точку В будет равна сумме работ на достаточно малых участках траектории:
.
Если раскрыть скобки и привести подобные, работа силы тяжести окажется равной разности потенциальных энергий:
.
Работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
Потенциальными или консервативными являются те силы, работа которых не зависит от формы траектории данного тела, а определяется лишь начальным и конечным положениями. Сила тяжести, сила упругости и электростатические силы являются примерами потенциальных сил.
 Рис. 3. Наклонная плоскость
Рис. 3. Наклонная плоскость
Вспомним один из знакомых нам простых
механизмов — наклонную плоскость (рис. 3). Наклонная плоскость даёт выигрыш в силе: при подъёме груза вдоль наклонной плоскости требуется меньшая сила, чем если поднимать данное тело вертикально, однако модуль перемещения в первом случае будет больше. Таким образом, наклонная плоскость не даёт выигрыша в работе: как при подъёме вдоль наклонной плоскости, так и при вертикальном подъёме будет совершена одинаковая работа, равная изменению потенциальной энергии груза.
Отметим, что, согласно теореме о кинетической энергии, работа равна разности конечной и начальной кинетической энергии:
.
В случае изменения потенциальной энергии работа равна разности начальной и конечной потенциальной энергии тела:
или .
Работа внутренних сил системы равна изменению потенциальной энергии системы, взятому со знаком «−»: .
Из формулы выше следует, что если потенциальная энергия системы возрастает Eпот > Eпот0, работа внутренних сил системы имеет отрицательное значение. Например, тело поднимают на некоторую высоту: потенциальная энергия камня увеличивается, сила тяжести совершает отрицательную работу.
Чтобы поднять камень, необходимо приложить некоторую силу. Таким образом, на камень действуют внешние силы, направление которых совпадает с направлением перемещения камня — внешние силы совершают положительную работу.
Потенциальная энергия деформированной пружины
 Рис. 4. Сила упругости совершает положительную работу
Рис. 4. Сила упругости совершает положительную работу
Пусть пружину жёсткостью k сжали на величину (рис. 4). Тогда на шарик, прикреплённый к пружине, действует сила , равная по модулю .
Под действием силы упругости пружина вернётся в недеформированное состояние — точку В. Сила упругости при этом совершит работу А. Пусть начальная потенциальная энергия Eпот0, конечная — Eпот. Тогда работа силы упругости равна
.
Потенциальная энергия недеформированной пружины равна нулю Eпот = 0, тогда работа силы упругости равна
.
Сила упругости, возникающая в пружине, прямо пропорциональна величине , следовательно, по мере движения шарика от точки А к точке В модуль силы упругости будет уменьшаться пропорционально её деформации от максимального значения вплоть до нуля .
На рисунке 5 показана зависимость модуля силы упругости от величины деформации пружины.
 Рис. 5. Зависимость модуля силы упругости от величины деформации пружины
Рис. 5. Зависимость модуля силы упругости от величины деформации пружины
Нам уже известно, что, если сила, действующая на тело, изменяется с течением времени, для вычисления работы такой силы перемещение необходимо разбить на достаточно малые промежутки времени, на каждом из которых силу можно считать величиной постоянной.
Пусть отрезок АВ представляет собой совокупность достаточно малых отрезков Δх0, Δх1, Δх2 … и т. д. (рис. 5, а). Тогда модуль силы упругости Fупрn на отрезке от хn до хn + Δxn можно считать неизменным во времени.
Работа силы упругости на рассматриваемом участке равна . Из рисунка видно, что работа равна площади заштрихованного прямоугольника .
Очевидно, что на каждом достаточно малом участке работа силы упругости будет равна площади соответствующего прямоугольника (рис. 5, б).
Общая работа равна сумме работ на достаточно малых промежутках, следовательно, общая работа равна сумме площадей полученных прямоугольников A = S1 + S2 + … + Sn. Чем больше вводится элементарных отрезков, тем точнее будет вычислена работа силы упругости. При разбиении на достаточно малые промежутки отрезка АВ сумма площадей всех прямоугольников будет приблизительно равна площади прямоугольного треугольника АВС:
.
Учитывая соотношение, получаем, что потенциальная энергия деформированной пружины равна
,
где Eпот0 [Дж] — потенциальная энергия деформированной пружины;
k [Н/м] — жёсткость пружины;
[м] — величина деформации (удлинение пружины).
Потенциальная энергия деформированной пружины вычисляется по формуле .
Пример 1
Камень массой 5 кг свободно падает вертикально вниз с высоты
см. Определите, какую работу совершила сила тяжести к моменту времени, когда камень находился на высоте см.
Решение
 Рис. 6. К примеру 1
Рис. 6. К примеру 1
1. Сделаем схематический рисунок, при этом примем рассматриваемое тело за материальную точку. Систему отсчёта свяжем с поверхностью Земли.
2. Запишем выражение для работы силы тяжести:
.
3. Подставляя исходные данные задачи в формулу для расчёта работы, получим окончательный ответ:
Дж.
4. Заметим, что тот же результат можно было получить, используя общее определение механической работы. Сила, совершающая работу, направлена вертикально вниз, туда же направлено и перемещение тела, тогда
Дж.
Ответ: А=7 Дж.
Итоги
- Потенциальная энергия тела — это энергия взаимодействия системы тел или частей одного тела друг с другом.
- Потенциальная энергия системы тел равна работе, которую совершают потенциальные силы взаимодействия её тел при переходе системы из данного состояния в состояние, потенциальная энергия которого равна нулю.
- Потенциальная энергия тела в поле тяжести Земли вычисляется по формуле .
- Работа внутренних сил системы равна изменению потенциальной энергии системы, взятому со знаком «−»: .
- Потенциальная энергия деформированной пружины вычисляется по формуле .
Упражнение 1
1. Определите потенциальную энергию:
а) тела массой 1,8 кг, поднятого над землёй на высоту 7 м;
б) деформированной пружины жёсткостью 600 Н/м, растянутой на 24 см от положения равновесия.
2. Пружину сжали на см от положения равновесия и отпустили. Какую работу совершила сила упругости к моменту времени, когда смещение от положения равновесия составляло см? Жёсткость пружины равна 400 Н/м.
Контрольные вопросы
1. В чём физический смысл потенциальной энергии?
2. Как связаны работа внутренних сил и потенциальная энергия тела?
3. По какой формуле вычисляется потенциальная энергия упруго деформированной пружины?
Упражнение 1
1. а) 126 Дж; б) 17,28 Дж
2. 4 Дж



