- Механическая энергия системы тел. Закон изменения механической энергии
- Закон сохранения механической энергии
- Примеры решения задач
- знать понятие «механическая энергия системы тел»; законы сохранения и изменения механической энергии системы
- уметь применять законы сохранения и изменения механической энергии системы при решении задач
- По какой формуле рассчитывается кинетическая энергия?
- По какой формуле рассчитывается потенциальная энергия тела в поле тяжести Земли?
- Какой энергией обладает тело, брошенное вертикально вверх в наивысшей точке траектории?
Механическая энергия системы тел. Закон изменения механической энергии
Тело, брошенное под углом к горизонту, на протяжении своего пути будет обладать и кинетической, и потенциальной энергией взаимодействия с Землёй.
Аналогично пружина, пришедшая в движении в результате деформации, обладает и кинетической, и потенциальной энергией деформированной пружины. Сумма двух видов энергий называется механической энергией системы Eмех:
.
Eмех [Дж] — механическая энергия тела;
Eпот [Дж] — потенциальная энергия тела;
Eкин [Дж] — кинетическая энергия тела.
Механическая энергия системы тел (тела) Eмех — это сумма кинетической и потенциальной энергии системы (тела): .
Пусть работа всех сил, действующих на материальную точку, равна А. Тогда в соответствии с теоремой о кинетической энергии справедливо следующее выражение:
,
где работа А всех сил представляет собой сумму работы внутренних потенциальных сил Aп, работы внутренних сил трения Aтр и работы внешних сил Aex:
.
С учётом выражения выше формула принимает следующий вид:
.
Работа потенциальных сил равна изменению потенциальной энергии системы, взятой со знаком минус:
.
Подставим это уравнение в формулу выше:
.
Запишем полученное выражение иначе:
.
Механическая энергия системы — это сумма кинетической и потенциальной энергии системы, начальная и конечная механические энергии системы соответственно равны:
и .
Тогда выражение можно записать в следующем виде:
.
Формула выше говорит о том, что механическая энергия системы изменится при совершении работы внутренними силами трения и в случае совершения работы над телами системы внешними силами.
Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения Aтр и внешних сил над телами системы Aex: .
Закон сохранения механической энергии
Закон сохранения механической энергии является следствием закона изменения механической энергии.
Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения Aтр и внешних сил над телами системы Aex равна нулю, то механическая энергия системы не изменяется: , при .
Закон сохранения энергии можно записать иначе:
.
Законы сохранения и изменения энергии позволяют облегчить решение задач кинематики и динамики.
Например, необходимо найти максимальную высоту H, на которую поднимется тело, брошенное под углом к горизонту.
Известно, что начальная скорость тела равна , скорость в наивысшей точке траектории — .
В начальный момент времени тело находится на Земле, следовательно, его потенциальная энергия равна нулю , начальная кинетическая энергия тела равна .
В наивысшей точке траектории потенциальная энергия тела равна , а кинетическая энергия .
Воспользуемся законом сохранения энергии:
.
Сократим обе части этого уравнения на массу и выразим искомую высоту:
.
Примеры решения задач
Пример 1
С крыши многоэтажного дома высотой 100 м бросили камень под углом 30° к горизонту с начальной скоростью 5 м/с. Найти модуль конечной скорости камня при его приземлении на Землю. Потерями энергии пренебречь.
Решение
1. Будем считать камень материальной точкой. Систему отсчёта свяжем с Землёй.
2. По условию задачи потерями энергии в процессе движения камня можно пренебречь, поэтому можно воспользоваться законом сохранения энергии:
.
3. Определим значения кинетической и потенциальной энергии камня в начальный и конечный моменты времени.
Камень бросают с высоты h = 100 м, следовательно, его начальная потенциальная энергия равна . Начальную скорость обозначим , тогда начальная кинетическая энергия равна
.
В момент приземления на Землю потенциальная энергия тела равна нулю , а кинетическая энергия равна .
4. Подставляем выражения, полученные для кинетических и потенциальных энергий, в формулу закона сохранения энергии и выражаем конечную скорость камня:
;
.
Ответ: .
Пример 2
После удара клюшкой шайба массой 200 г въезжает на наклонную ледяную плоскость с начальной скоростью 20 м/с. Угол наклона плоскости составляет 45° с горизонтом, коэффициент трения шайбы о лёд равен 0,4. Найти максимальную высоту, на которую поднимется шайба до полной потери скорости.
Решение
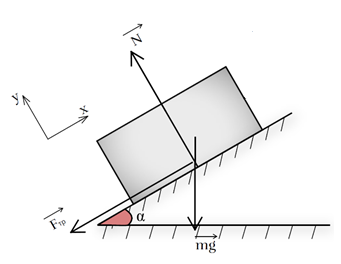 Рис. 1. Иллюстрация к примеру 2
Рис. 1. Иллюстрация к примеру 2
1. Будем считать шайбу материальной точкой. Систему отсчёта свяжем с Землёй, ось ОХ направим вдоль наклонной плоскости в направлении движения шайбы (рис. 1).
Изобразим силы, действующие на шайбу: сила трения, сила тяжести и сила реакции опоры.
2. На шайбу не действуют внешние силы, но есть потери механической энергии на трение. Закон изменения механической энергии будет иметь следующий вид:
или
.
3. Найдём работу силы трения:
.
Перемещение тела вдоль наклонной плоскости Δх можно найти через синус угла и высоту h, на которую поднимется шайба:
;
.
Силу трения можно найти по следующей формуле:
,
тогда с учётом формул выше работа силы трения равна:
.
4. Определим значения кинетической и потенциальной энергии шайбы в начальный и конечный моменты времени.
У основания наклонной плоскости потенциальная энергия шайбы равна нулю . Начальная кинетическая энергия шайбы равна .
В наивысшей точке подъёма скорость шайбы равна нулю , потенциальная энергия равна .
5. Подставляем выражения, полученные для кинетических и потенциальных энергий, а также соотношение выше в формулу и выражаем искомую высоту:
;
.
Ответ: .
Итоги
- Механическая энергия системы тел — это сумма кинетической и потенциальной энергии системы (тела): .
- Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
- Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения и внешних сил над телами системы Aex равна нулю, то механическая энергия системы не изменяется: , при .
Упражнение 1
1. Тело массой 5 кг свободно падает с высоты 10 м. Найти потенциальную и кинетическую энергию тела на высоте 4 м от поверхности Земли. Потерями энергии в процессе движения пренебречь.
2. При подготовке пружинного пистолета к выстрелу пружину жёсткостью 2 кН/м сжали на 2 см. Какую скорость приобретёт пуля массой 200 г в момент выстрела? Потерями энергии пренебречь.
3. Санки с человеком общей массой 70 кг скатываются с горы высотой
10 м и длиной 80 м. Найти силу трения, действующую на санки, если в конце спуска они развили скорость 5 м/с, а на вершине горы их скорость была равна нулю.
Контрольные вопросы
1. Что такое механическая энергия системы тел?
2. Сформулируйте закон изменения механической энергии.
3. Сформулируйте закон сохранения механической энергии.
Упражнение 1
1. Eпот = 200 Дж; Eкин = 300 Дж
2. = 2 м/с
3. Fтр = 76,6 Н
- Механическая энергия системы тел. Закон изменения механической энергии
- Закон сохранения механической энергии
- Примеры решения задач
- знать понятие «механическая энергия системы тел»; законы сохранения и изменения механической энергии системы
- уметь применять законы сохранения и изменения механической энергии системы при решении задач
- По какой формуле рассчитывается кинетическая энергия?
- По какой формуле рассчитывается потенциальная энергия тела в поле тяжести Земли?
- Какой энергией обладает тело, брошенное вертикально вверх в наивысшей точке траектории?
Механическая энергия системы тел. Закон изменения механической энергии
Тело, брошенное под углом к горизонту, на протяжении своего пути будет обладать и кинетической, и потенциальной энергией взаимодействия с Землёй.
Аналогично пружина, пришедшая в движении в результате деформации, обладает и кинетической, и потенциальной энергией деформированной пружины. Сумма двух видов энергий называется механической энергией системы Eмех:
.
Eмех [Дж] — механическая энергия тела;
Eпот [Дж] — потенциальная энергия тела;
Eкин [Дж] — кинетическая энергия тела.
Механическая энергия системы тел (тела) Eмех — это сумма кинетической и потенциальной энергии системы (тела): .
Пусть работа всех сил, действующих на материальную точку, равна А. Тогда в соответствии с теоремой о кинетической энергии справедливо следующее выражение:
,
где работа А всех сил представляет собой сумму работы внутренних потенциальных сил Aп, работы внутренних сил трения Aтр и работы внешних сил Aex:
.
С учётом выражения выше формула принимает следующий вид:
.
Работа потенциальных сил равна изменению потенциальной энергии системы, взятой со знаком минус:
.
Подставим это уравнение в формулу выше:
.
Запишем полученное выражение иначе:
.
Механическая энергия системы — это сумма кинетической и потенциальной энергии системы, начальная и конечная механические энергии системы соответственно равны:
и .
Тогда выражение можно записать в следующем виде:
.
Формула выше говорит о том, что механическая энергия системы изменится при совершении работы внутренними силами трения и в случае совершения работы над телами системы внешними силами.
Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения Aтр и внешних сил над телами системы Aex: .
Закон сохранения механической энергии
Закон сохранения механической энергии является следствием закона изменения механической энергии.
Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения Aтр и внешних сил над телами системы Aex равна нулю, то механическая энергия системы не изменяется: , при .
Закон сохранения энергии можно записать иначе:
.
Законы сохранения и изменения энергии позволяют облегчить решение задач кинематики и динамики.
Например, необходимо найти максимальную высоту H, на которую поднимется тело, брошенное под углом к горизонту.
Известно, что начальная скорость тела равна , скорость в наивысшей точке траектории — .
В начальный момент времени тело находится на Земле, следовательно, его потенциальная энергия равна нулю , начальная кинетическая энергия тела равна .
В наивысшей точке траектории потенциальная энергия тела равна , а кинетическая энергия .
Воспользуемся законом сохранения энергии:
.
Сократим обе части этого уравнения на массу и выразим искомую высоту:
.
Примеры решения задач
Пример 1
С крыши многоэтажного дома высотой 100 м бросили камень под углом 30° к горизонту с начальной скоростью 5 м/с. Найти модуль конечной скорости камня при его приземлении на Землю. Потерями энергии пренебречь.
Решение
1. Будем считать камень материальной точкой. Систему отсчёта свяжем с Землёй.
2. По условию задачи потерями энергии в процессе движения камня можно пренебречь, поэтому можно воспользоваться законом сохранения энергии:
.
3. Определим значения кинетической и потенциальной энергии камня в начальный и конечный моменты времени.
Камень бросают с высоты h = 100 м, следовательно, его начальная потенциальная энергия равна . Начальную скорость обозначим , тогда начальная кинетическая энергия равна
.
В момент приземления на Землю потенциальная энергия тела равна нулю , а кинетическая энергия равна .
4. Подставляем выражения, полученные для кинетических и потенциальных энергий, в формулу закона сохранения энергии и выражаем конечную скорость камня:
;
.
Ответ: .
Пример 2
После удара клюшкой шайба массой 200 г въезжает на наклонную ледяную плоскость с начальной скоростью 20 м/с. Угол наклона плоскости составляет 45° с горизонтом, коэффициент трения шайбы о лёд равен 0,4. Найти максимальную высоту, на которую поднимется шайба до полной потери скорости.
Решение
 Рис. 1. Иллюстрация к примеру 2
Рис. 1. Иллюстрация к примеру 2
1. Будем считать шайбу материальной точкой. Систему отсчёта свяжем с Землёй, ось ОХ направим вдоль наклонной плоскости в направлении движения шайбы (рис. 1).
Изобразим силы, действующие на шайбу: сила трения, сила тяжести и сила реакции опоры.
2. На шайбу не действуют внешние силы, но есть потери механической энергии на трение. Закон изменения механической энергии будет иметь следующий вид:
или
.
3. Найдём работу силы трения:
.
Перемещение тела вдоль наклонной плоскости Δх можно найти через синус угла и высоту h, на которую поднимется шайба:
;
.
Силу трения можно найти по следующей формуле:
,
тогда с учётом формул выше работа силы трения равна:
.
4. Определим значения кинетической и потенциальной энергии шайбы в начальный и конечный моменты времени.
У основания наклонной плоскости потенциальная энергия шайбы равна нулю . Начальная кинетическая энергия шайбы равна .
В наивысшей точке подъёма скорость шайбы равна нулю , потенциальная энергия равна .
5. Подставляем выражения, полученные для кинетических и потенциальных энергий, а также соотношение выше в формулу и выражаем искомую высоту:
;
.
Ответ: .
Итоги
- Механическая энергия системы тел — это сумма кинетической и потенциальной энергии системы (тела): .
- Закон изменения механической энергии системы тел: изменение механической энергии системы тел равно сумме работ внутренних сил трения и внешних сил над телами системы : .
- Закон сохранения механической энергии системы тел: если сумма работ внутренних сил трения и внешних сил над телами системы Aex равна нулю, то механическая энергия системы не изменяется: , при .
Упражнение 1
1. Тело массой 5 кг свободно падает с высоты 10 м. Найти потенциальную и кинетическую энергию тела на высоте 4 м от поверхности Земли. Потерями энергии в процессе движения пренебречь.
2. При подготовке пружинного пистолета к выстрелу пружину жёсткостью 2 кН/м сжали на 2 см. Какую скорость приобретёт пуля массой 200 г в момент выстрела? Потерями энергии пренебречь.
3. Санки с человеком общей массой 70 кг скатываются с горы высотой
10 м и длиной 80 м. Найти силу трения, действующую на санки, если в конце спуска они развили скорость 5 м/с, а на вершине горы их скорость была равна нулю.
Контрольные вопросы
1. Что такое механическая энергия системы тел?
2. Сформулируйте закон изменения механической энергии.
3. Сформулируйте закон сохранения механической энергии.
Упражнение 1
1. Eпот = 200 Дж; Eкин = 300 Дж
2. = 2 м/с
3. Fтр = 76,6 Н

