Конспект урока: Кинетическая энергия

Кинетическая энергия

Нам уже известно, что при совершении положительной работы над материальной точкой её скорость увеличивается, при совершении отрицательной работы — уменьшается. Определим математическую связь между работой и изменением скорости тела.

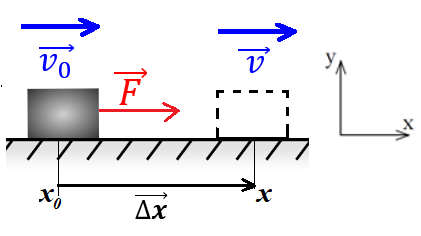Рис. 1. Сила F совершает положительную работу над телом

Пусть тело массой m движется в положительном направлении оси ОХ (рис. 1). Начальная скорость тела равна ${\overrightarrow{v}}_0$. На тело начинает действовать постоянная сила $\overrightarrow{F}$, сонаправленная с вектором перемещения $∆\overrightarrow{x}$. В данном случае сила совершает положительную работу, следовательно, тело приобретёт некоторое положительное ускорение, которое можно найти по второму закону Ньютона:

$a=\frac{F}{m}$.

Скорость тела через время t можно найти по закону изменения скорости для равноускоренного движения:
 

$\overrightarrow{v}={\overrightarrow{v}}_0+\overrightarrow{a}·t$.
 

Запишем выражение в проекциях на ось ОХ:
 

$v=v_0+a·t$.
 

Проекция модуля перемещения тела на ось ОХ за время t равна:
 

$∆x=v_0·t+\frac{a·t^2}{2}$.
 

Выразим из формулы скорости время t и подставим полученное выражение в формулу выше:
 

$∆x=v_0·\left(\frac{v-v_0}{a}\right)+\frac{a·{\left(v-v_0\right)}^2}{2a^2}=\frac{v_0·2a·\left(v-v_0\right)}{2a^2}+\frac{a·{\left(v-v_0\right)}^2}{2a^2}=\frac{v^2-{v_0}^2}{2a}$.
 

Умножим обе части уравнения на F и учтём, что по второму закону Ньютона $F=m·a$:

$F·∆x=F·\frac{v^2-{v_0}^2}{2a}\iff A=m·a·\frac{v^2-{v_0}^2}{2a}\iff A=\frac{m·v^2}{2}-\frac{m·{v_0}^2}{2}$.

Физическая величина, равная $\frac{m·v^2}{2}$, называется кинетической энергией тела E_кин:

$E_{\mathrm{кин}}=\frac{m·v^2}{2}$,

где $E_{кин} \left[Дж\right]$ — кинетическая энергия тела;
$m \left[кг\right]$ — масса тела;
$v \left[\raisebox{1ex}{$м$}\!\left/ \!\raisebox{-1ex}{$с$}\right.\right]$ — скорость тела в инерциальной системе отсчёта.

Таким образом, работа, совершённая над телом, равна изменению его кинетической энергии в инерциальной системе отсчёта:
 

$A=E_{\mathrm{кин}}-E_{\mathrm{кин}0}=∆E_{\mathrm{кин}}$.
 

Выражение выше можно записать иначе:
 

$E_{\mathrm{кин}0}+A=E_{\mathrm{кин}}$.
 

Из этого соотношения видно, что от знака работы зависит увеличение кинетической энергии тела или уменьшение: если над телом совершена положительная работа А > 0, то конечная кинетическая энергия тела увеличится E_кин > E_кин0, скорость тела возрастёт. Напротив, если над телом совершить отрицательную работу, скорость тела снизится.

Будет ли справедливо выражение выше в случае, когда между вектором силы $\overrightarrow{F}$ и вектором перемещения $∆\overrightarrow{x}$ есть некоторый угол $\alpha$, отличный от нуля?

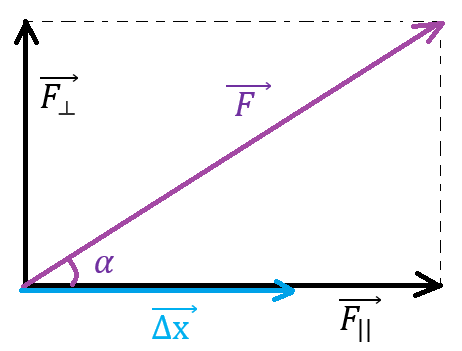Рис. 2. Сила F || равна проекции силы F на вектор перемещения

Рассмотрим действие такой силы (рис. 2).

Любую силу $\overrightarrow{F}$, действующую на тело, можно представить как сумму двух взаимно перпендикулярных векторов ${\overrightarrow{F}}_{\parallel }$ и ${\overrightarrow{F}}_{\perp }$, один из которых ${\overrightarrow{F}}_{\parallel }$ сонаправлен с вектором перемещения $∆\overrightarrow{r}$, а второй ${\overrightarrow{F}}_{\perp }$ — перпендикулярен ему.

Работа силы $\overrightarrow{F}$ равна $A=F·∆x·\cos \left(\alpha \right)$, работа силы ${\overrightarrow{F}}_{\parallel }$ равна $A=F_{\parallel }·∆x$. Понятно, что $F_{\parallel }$ есть проекция силы F на вектор перемещения $F_{\parallel }=F·\cos \left(\alpha \right)$, следовательно, работы сил ${\overrightarrow{F}}_{\parallel }$ и $\overrightarrow{F}$ равны. Получается, именно сила ${\overrightarrow{F}}_{\parallel }$ обуславливает изменение кинетической энергии тела.
 

С другой стороны, работа силы ${\overrightarrow{F}}_{\perp }$ равна нулю: $A=F_{\perp }·∆x·\cos (90°)=0$. Следовательно, сила ${\overrightarrow{F}}_{\perp }$ не влияет ни на модуль скорости, ни на кинетическую энергию тела.

Выясним, в чём заключается физический смысл кинетической энергии.
 

Пусть материальная точка покоится в инерциальной системе отсчёта. В этом случае её начальная кинетическая энергия также равна нулю Е_кин0 = 0. При совершении над материальной точкой работы А её кинетическая энергия будет равна совершённой работе:

$A=E_{\mathrm{кин}}-E_{\mathrm{кин}0}=E_{\mathrm{кин}}=\frac{m·v^2}{2}$.

Справедливо и обратное утверждение. Если в инерциальной системе отсчёта материальная точка имеет некоторую скорость $v$, то при совершении над точкой отрицательной работы А, равной её начальной кинетической энергии, конечная кинетическая энергия данной точки станет равна нулю. В процессе торможения материальная точка совершит положительную работу, равную по модулю работе тормозящих сил.

Рассмотрим систему материальных точек, имеющих скорости, отличные от нуля. Кинетические энергии точек равны соответственно $E_{\mathrm{кин}1}=\frac{m_1·{v_1}^2}{2}$, $E_{\mathrm{кин}2}=\frac{m_2·{v_2}^2}{2}$ … $E_{\mathrm{кин}n}=\frac{m_n·{v_n}^2}{2}$. Каждая из этих точек при уменьшении своей скорости до нуля сможет совершить работу, равную её кинетической энергии: А₁ = Е_кин1, А₂ = Е_кин2 …, А_n = Е_кинn. Тогда система материальных точек совершит работу, равную $A=A_1+A_2+...+A_n=E_{\mathrm{кин}1}+E_{\mathrm{кин}2}+...+E_{\mathrm{кин}n}$. Таким образом, работа системы материальных точек равна сумме кинетических энергий всех точек системы.

Пример решения задачи

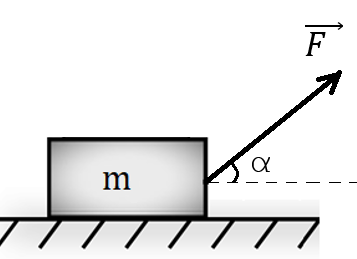Рис. 3. Иллюстрация к примеру

К телу, расположенному на гладкой горизонтальной поверхности приложена сила F, направленная под углом 60° к горизонту (рис. 3). Масса тела равна 40 кг. Определить модуль силы F, если известно, что после перемещения тела на 5 м модуль скорости тела увеличился от 2 до 12 м/с.

Итоги

• Кинетическая энергия тела E_кин — это физическая величина, равная половине произведения массы тела на квадрат его скорости: $E_{\mathrm{кин}}=\frac{m·v^2}{2}$.
• Теорема о кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении: $A=∆E_{\mathrm{кин}}$.
• Кинетическая энергия материальной точки равна работе А, которую она может совершить над другими телами при уменьшении своей скорости до нуля.
• Кинетическая энергия системы материальных точек равна сумме их кинетических энергий: $E_{\mathrm{кин}}=E_{\mathrm{кин}1}+E_{\mathrm{кин}2}+...+E_{\mathrm{кин}n}$.