- Вклад в математику Герона Александрийского
- Формула Герона
- Примеры применения формулы Герона
- Знать формулу Герона
- Уметь применять формулу Герона для решения задач
- Как вычислить площадь треугольника?
- Выразите катет прямоугольного треугольника через гипотенузу и другой катет?
- Как разложить на множители разность квадратов?
Историческая справка
 Рис. 1. Герон Александрийский
Рис. 1. Герон Александрийский
Геро́н Александри́йский (др.-греч. Ἥρων ὁ Ἀλεξανδρεύς) — греческий математик и механик (Рис. 1).
Время жизни отнесено ко второй половине I века н. э. на том основании, что он приводит в качестве примера лунное затмение 13 марта 62 г. н. э. Подробности его жизни неизвестны.
Герона относят к величайшим инженерам за всю историю человечества. Он первым изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации, прибор для измерения протяжённости дорог (древний одометр) и др. Первым начал создавать программируемые устройства: вал со штырьками с намотанной на него верёвкой.
Занимался геометрией, механикой, гидростатикой, оптикой. Основные произведения: «Метрика», «Пневматика», «Автоматопоэтика», «Механика» (произведение сохранилось целиком в арабском переводе), «Катоптрика» (наука о зеркалах; сохранилась только в латинском переводе) и др. В 1814 году было найдено сочинение Герона «О диоптре», в котором изложены правила земельной съёмки, фактически основанные на использовании прямоугольных координат. Герон использовал достижения своих предшественников: Евклида, Архимеда, Стратона из Лампсака.
Многие из его книг безвозвратно утеряны (свитки содержались в Александрийской библиотеке). Одна из копий его книг, сделанная в XVI веке, содержится в Оксфордском Университете.
В средние века многие из его изобретений были отвергнуты, забыты или не представляли практического интереса.
«Метрика» (Μετρική) Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений:
- Целочисленные героновы треугольники.
- Формулы для площадей правильных многоугольников.
- Объёмы правильных многогранников, пирамиды, конуса, усечённого конуса, тора, шарового сегмента.
- Формула Герона для расчёта площади треугольника по длинам его сторон (открытая Архимедом).
- Правила численного решения квадратных уравнений.
- Алгоритмы извлечения квадратных и кубических корней.
В основном изложение в математических трудах Герона догматично: правила часто не выводятся, а только показываются на примерах.
Книга Герона «Определения» представляет собой обширный свод геометрических определений, по большей части совпадающих с определениями «Начал» Евклида.
Теорема (формула Герона)
Площадь треугольника со сторонами , , выражается формулой
,
где — полупериметр треугольника.
Доказательство
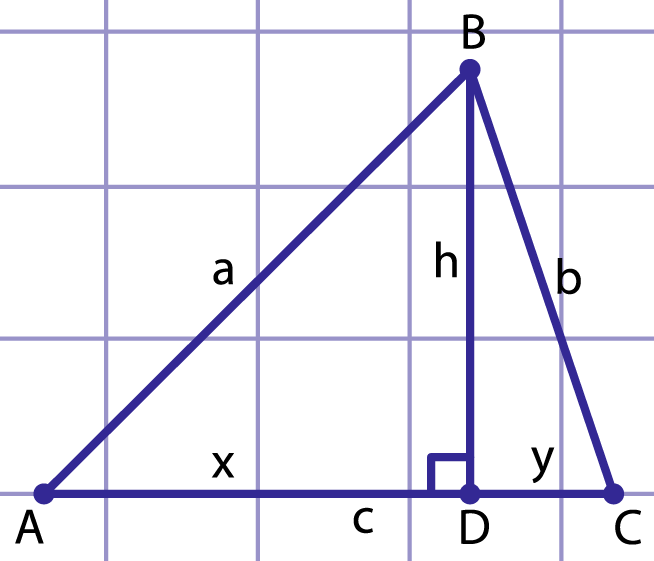 Рис. 2. К доказательству формулы Герона
Рис. 2. К доказательству формулы Герона
Рассмотрим треугольник , в котором , , , . Пусть углы и острые, проведем высоту из вершины большего угла треугольника.
Обозначим , (Рис. 2). По теореме Пифагора выразим высоту из прямоугольных треугольников и :
.
Следовательно, , откуда . Так как , то . Выразим , сложив два последних равенства и поделив на :
.
Тогда,
.
Поскольку
,
то и , , .
Тогда
.
Следовательно,
.
.
Теорема доказана.
Пример 1
Найдите площадь треугольника со сторонами , , .
Решение
Для вычисления площади используем формулу Герона:
.
.
Ответ: .
Пример 2
Найдите наименьшую высоту треугольника со сторонами , и .
Решение
Для решения задачи используем метод площадей: вычислим площадь треугольника, используя формулу Герона, а после, используя теорему о площади треугольника, вычислим высоту треугольника. Поскольку площадь треугольника величина постоянная, то меньшая высота проведена к большей стороне.
,
.
Обозначим искомую высоту :
, .
Ответ: .
Пример 3
Основания трапеции равны и , а боковые стороны — и . Найдите площадь трапеции.
Решение
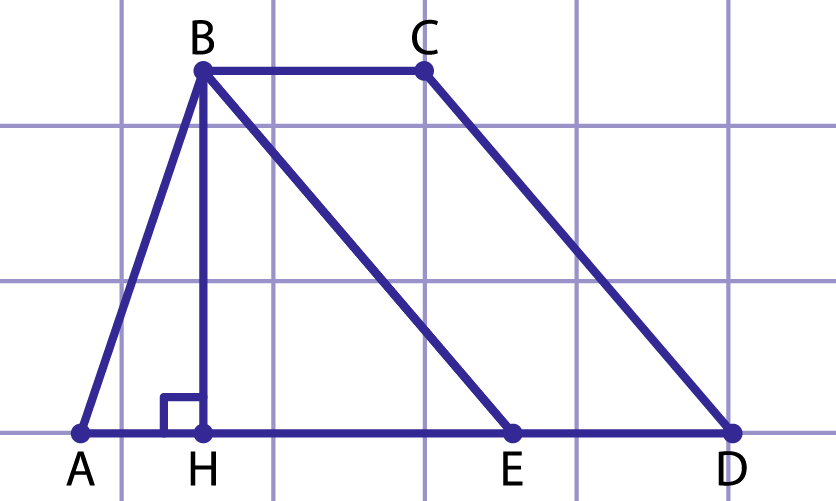 Рис. 3. К решению примера 3
Рис. 3. К решению примера 3
Рассмотрим трапецию , , , , (Рис. 3). Проведем прямую параллельную , по определению — параллелограмм, тогда , .
.
Высота треугольника совпадает с высотой трапеции . Вычислим высоту как показано в примере 2 с применением формулы Герона:
.
.
.
Зная высоту и длины оснований трапеции, вычислим площадь:
.
Ответ: .
Упражнения
1. Найдите площадь треугольника со сторонами , , .
2. Найдите наименьшую высоту треугольника со сторонами , и .
3. Вычислите площадь параллелограмма, стороны которого равны и , а одна из диагоналей равна .
Контрольные вопросы
1. Сформулируйте формулу Герона.
2. Приведите пример задачи, в которой площадь треугольника можно вычислить с помощью формулы Герона, но нельзя вычислить с помощью теоремы о площади треугольника.
1. .
2. .
3. .

