- Смежные и вертикальные углы;
- Перпендикулярные прямые;
- Построение прямых углов на местности.
- Знать определение смежных углов и свойство смежных углов;
- Знать определение вертикальных углов и их свойство;
- Знать определение перпендикулярных прямых;
- Уметь строить смежные углы, вертикальные углы, перпендикулярные прямые;
- Уметь применять свойства смежных углов, вертикальных углов, определение перпендикулярных прямых при решении задач.
- Назовите виды углов.
- Сколько общих точек имеют пересекающиеся прямые?
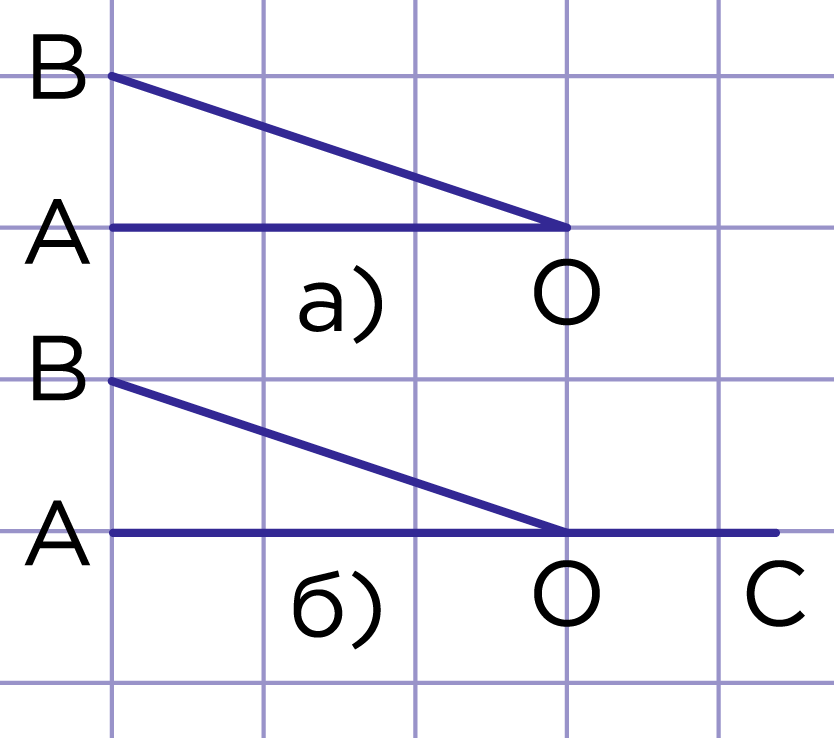Рис. 1. Луч ОС - продолжение луча ОА
Смежные и вертикальные углы
На рис. 1а изображён угол . Продолжим луч за точку .
На рис. 1б видим два угла: и , которые образуют развёрнутый : .
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными .
Сумма смежных углов равна .
На рисунке 1б углы и - смежные.
Пример 1
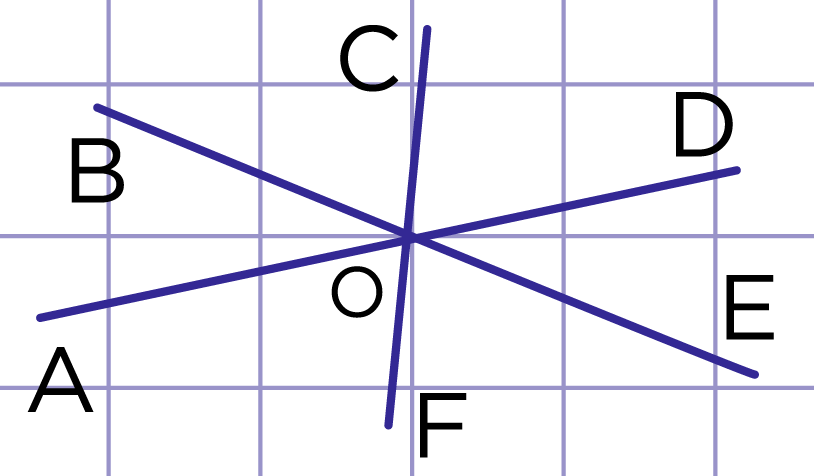Рис. 2. Пример 1
Назовите несколько пар смежных углов, изображённых на рисунке 2.
Решение
- и - смежные, т. к. – общая сторона, – продолжение ( - развёрнутый);
- и - смежные, т. к. – общая сторона, – продолжение ( - развёрнутый); и т. д.
Ответ: и ; и ; и т.д. (всего 6 пар смежных углов).
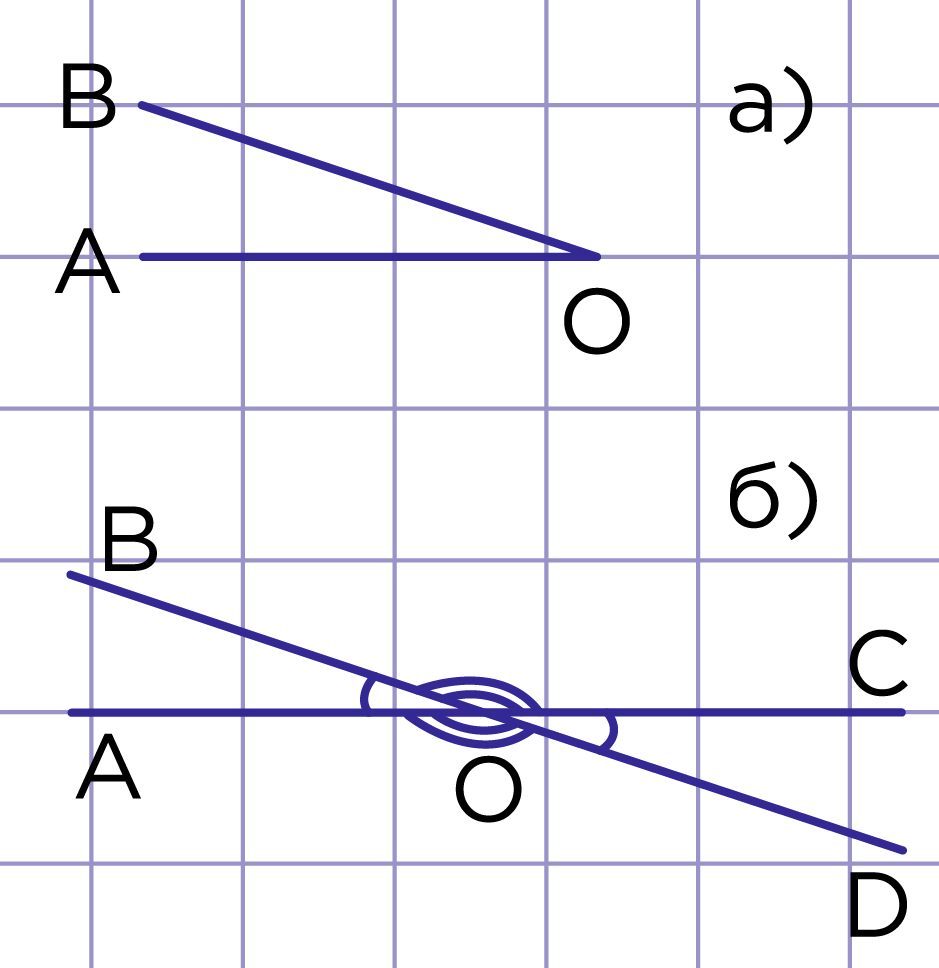Рис. 3. ОС – продолжение ОА, ОD – продолжение ОВ
Продолжим у заданного угла (рис. 3а) обе стороны: и луч , и луч за точку . Получим четыре неразвёрнутых угла: и (рис. 3б). Среди них выберем пары смежных углов:
, отсюда .
, отсюда . Тогда .
Если стороны одного угла являются продолжениями сторон другого, то такие углы называются вертикальными .
Вертикальные углы равны.
На рис. 3б и – вертикальные, и – вертикальные.
Пример 2
Найдите пару острых вертикальных углов и пару тупых вертикальных углов, изображённых на рисунке 2.
Ответ: и – острые вертикальные; и – тупые вертикальные углы.
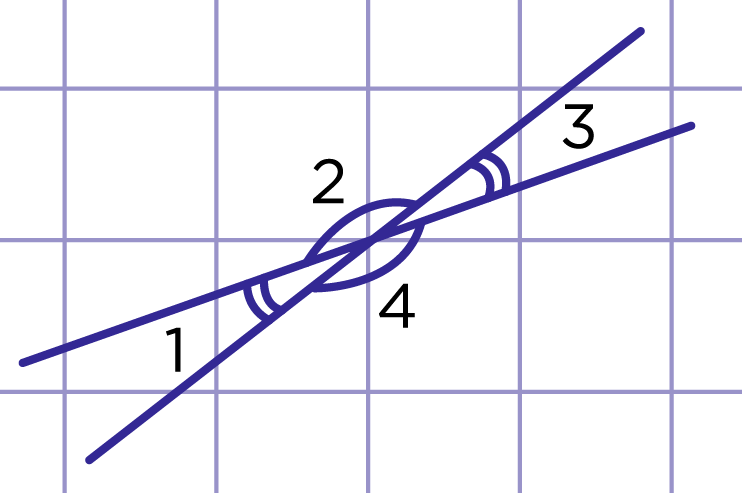Рис. 4. Углы при пересечении двух прямых
Перпендикулярные прямые
При пересечении двух прямых образуются четыре неразвёрнутых угла (рис. 4), среди которых можно отметить две пары вертикальных углов: и , и . Нетрудно проверить, что если один из них прямой, то и остальные углы – прямые
Две пересекающиеся прямые называются перпендикулярными , если они образуют четыре прямых угла.
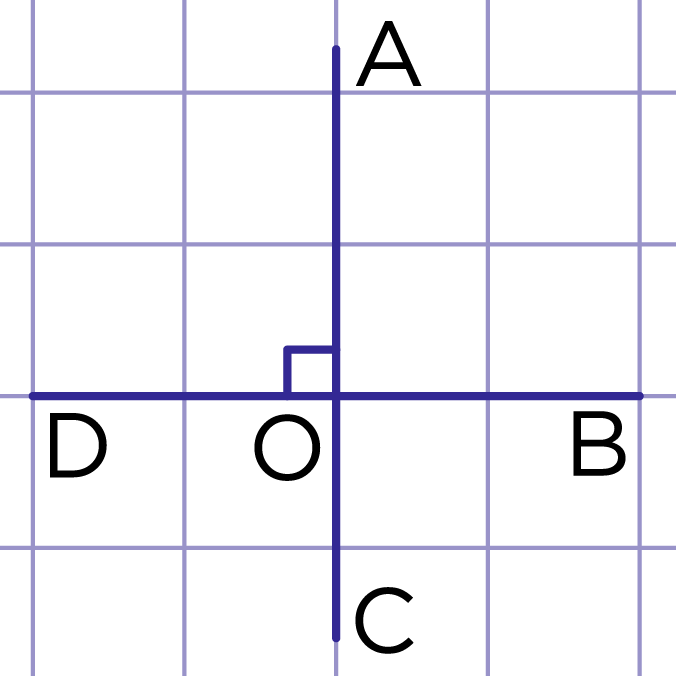Рис. 5. Перпендикулярные прямые
На рис. 5 прямые и перпендикулярны (пишут так: ). Запись читают так: "прямые и перпендикулярны или прямая перпендикулярна прямой ".
Отрезки (или лучи), лежащие на перпендикулярных прямых, будут перпендикулярны.
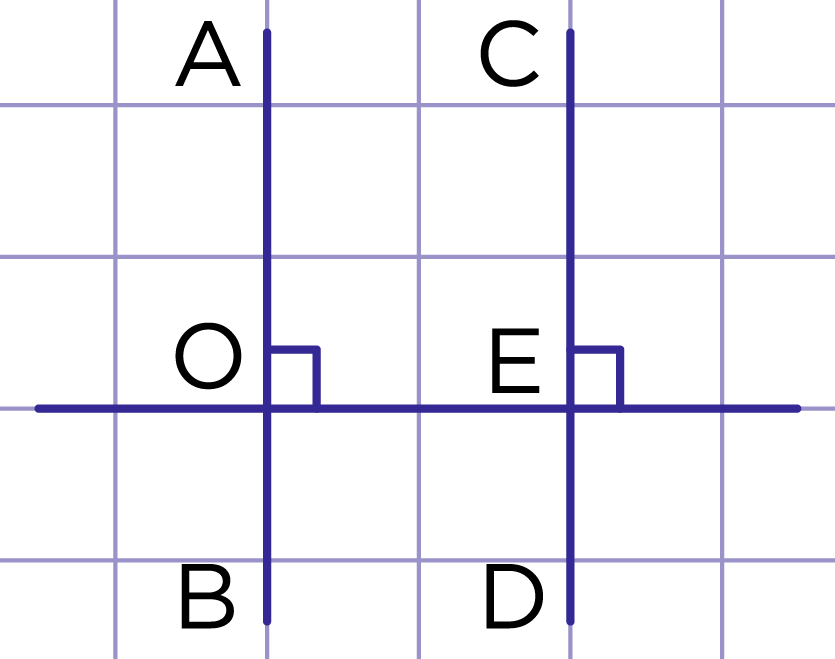Рис. 6. Две прямые, перпендикулярные к третьей прямой
Две прямые, перпендикулярные к третьей, не пересекаются (рис. 6).
Упражнение 1
1. Градусные меры углов и , изображённых на рис. 7, относятся как 1:5. Найдите эти углы.
2. На рис. 8 . – биссектриса . а) Найдите . б) Сравните углы и .
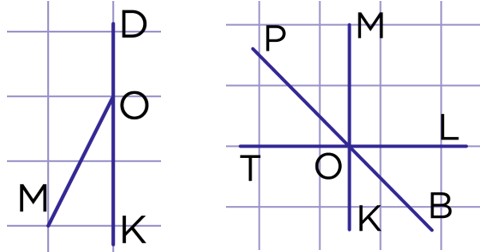Рис. 7. Рис 8.
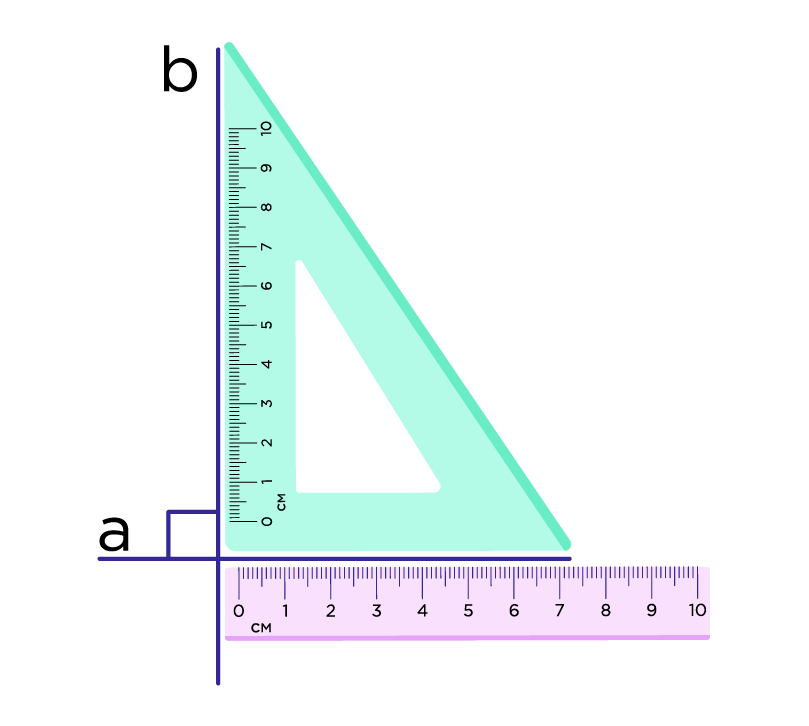Рис. 9. Построение перпендикулярных прямых
Построение прямых углов на местности
Для построения перпендикулярных прямых на бумаге используют чертёжный угольник и линейку.
Экер служит для построения прямых углов на местности.
Основная его часть – это бруски, закреплённые под прямым углом, на концах которых вбиты гвозди. Прямые, проходящие через гвозди, взаимно перпендикулярны.
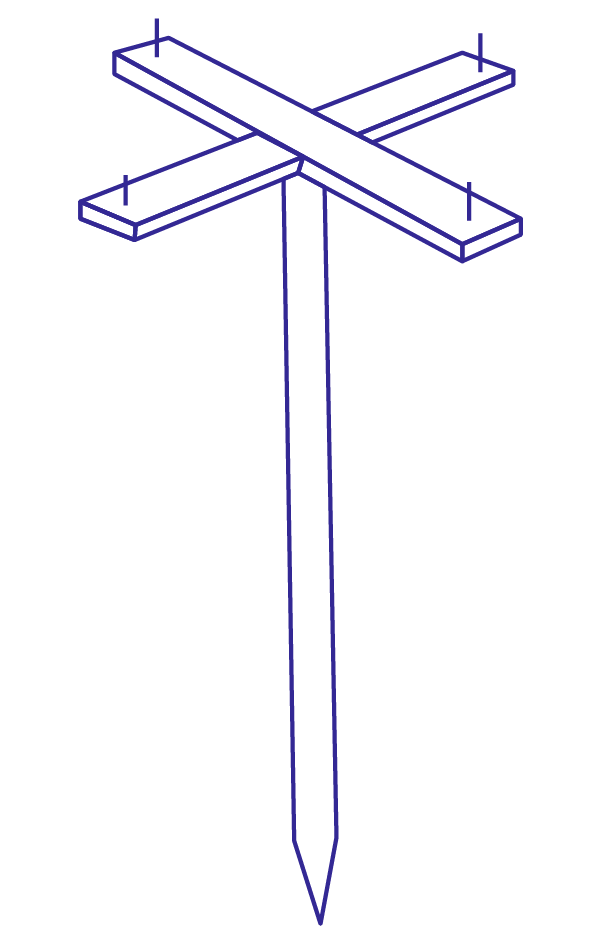Рис. 10. Экер
Прибор устанавливают в вершину угла. Направление луча на местности (одной из сторон угла, который надо построить), совмещают с направлением одного из брусков. Вторую сторону провешивают по направлению другого бруска.
Для построения прямых углов на местности существуют и более совершенные приборы, например теодолит .
Контрольные вопросы
1. Какие углы называются смежными?
2. Каким свойством они обладают?
3. Какие углы называются вертикальными?
4. Каким свойством они обладают?
5. Какие прямые называются перпендикулярными?
Упражнение 1
- а) ; б) равны.
