Теоремы об отрезках, связанных с окружностью. Углы с вершинами внутри и вне круга

План урока

Теоремы об отрезках, связанных с окружностью;
Углы с вершинами внутри и вне круга.

Цели урока

Знать формулировки теорем об отрезках, связанных с окружностью, и уметь их доказывать;
Знать, как выражаются углы с вершинами внутри и вне круга через заключённые внутри них дуги;
Уметь применять изученные теоремы при решении задач.

Разминка

Какую прямую называют секущей к окружности?
Какую прямую называют касательной к окружности?
Что такое хорда окружности?
Как связаны центральный и вписанный углы, опирающиеся на одну дугу окружности?

Теоремы об отрезках, связанных с окружностью

Сформулируем и докажем две теоремы.

Теорема 1

Произведение отрезков одной из двух пересекающихся хорд равно произведению отрезков другой хорды.

Доказательство

Рис. 1.

Известно, что некоторые хорды $M N$ и $E F$ пересекаются в точке $K$ (рис. 1). Требуется доказать, что $M K \cdot N K = E K \cdot F K$ .

Рассмотрим треугольники $M F K$ и $E N K$ .

$∠ 1 = ∠ 2$ (вертикальные), $∠ 3 = ∠ 4$ (опираются на одну и ту же дугу $N F$ ).

Следовательно, $∆ M F K ~ ∆ E N K$ по двум углам.

Тогда $\frac{M K}{E K} = \frac{F K}{N K} \Rightarrow M K \cdot N K = E K \cdot F K$ .

Теорема доказана.

Теорема 2

Если через точку $S$ проведены секущая, пересекающая окружность в точках $M$ и $N$ и касательная $S K$ ( $K$ – точка касания), то $S K^{2} = S M \cdot S N$ (рис. 2).

Доказательство

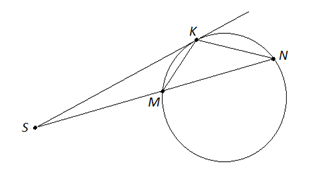Рис. 2.

Пусть из некоторой точки $S$ проведены секущая, пересекающая окружность в точках $M$ и $N$ , и касательная $S K$ ( $K$ – точка касания). Требуется доказать, что $S N \cdot S M = S K^{2}$ .

Рассмотрим треугольники $M K S$ и $K N S$ .

$∠ S$ – общий, $∠ M K S = ∠ K N S$ (каждый из них равен половине дуги $M K$ ) $\Rightarrow ∆ M K S ~ ∆ K N S$ по двум углам.

Тогда $\frac{S K}{S N} = \frac{S M}{S K} \Rightarrow S N \cdot S M = S K^{2}$ .

Теорема доказана.

Пример 1

Хорда $C D$ , перпендикулярная диаметру $A B$ , пересекает этот диаметр в точке $E$ (рис. 3). Найдите хорду $C D$ , если $A E = 9$ , $B E = 16$ .

Решение

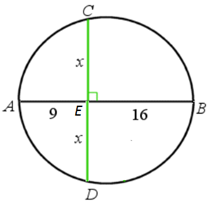Рис. 3.

По условию хорда $C D$ перпендикулярна диаметру $A B$ , тогда, опираясь на симметрию окружности относительно диаметра, можно сделать вывод, что $C E = D E$ . Обозначим $C E$ за $x$ .

Из теоремы об отрезках пересекающихся хорд (теорема 1) следует, что $C E \cdot D E = A E \cdot B E$ .

Тогда

$x^{2} = 9 \cdot 16$

$x = 3 \cdot 4$

$x = 12$

Таким образом, $C E = 12 \Rightarrow C D = 24$ .

Ответ: $24$ .

Пример 2

Через вершины $A$ и $С$ треугольника $A B C$ проходит окружность, пересекающая сторону $A B$ в точке $D$ и касающаяся стороны $B C$ . Найдите $A D$ , если $A C = 8$ , $B C = 6$ , $D C = 4, 8$ .

Решение

Рис. 4.

Так как окружность по условию задачи проходит через вершину $C$ и при этом касается стороны $B C$ , то это означает, что точка $C$ и является точкой касания окружности (рис. 4).

Треугольники $A B C$ и $C B D$ подобны по двум углам
( $∠ B$ – общий, $∠ C A B = ∠ D C B$ ). Из подобия этих треугольников следует

$\frac{B C}{B D} = \frac{A C}{D C} \Rightarrow B D = \frac{B C \cdot D C}{A C} = \frac{6 \cdot 4, 8}{8} = 3, 6$ .

Из теоремы о квадрате отрезка касательной (Теорема 2) следует

$A B \cdot B D = B C^{2} \Rightarrow A B = \frac{B C^{2}}{B D} = \frac{36}{3, 6} = 10$ .

$A D = 10 - 3, 6 = 6, 4$ .

Ответ: $6, 4$ .

Свойство секущих окружности

Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть.

Упражнение 1

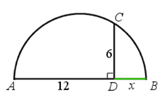Рис. 5.

На рисунке 5 изображена полуокружность с диаметром $A B$ . Найдите $x$ .
Через вершины $A$ и $C$ треугольника $A B C$ проходит окружность, пересекающая сторону $A B$ в точке $D$ и касающаяся стороны $B C$ . Найдите $A D$ , если $A C = 18$ , $B C = 18$ , $D C = 6 \sqrt{3}$ .

Углы с вершинами внутри и вне круга

Теорема 3

Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, заключённых между этими хордами.

Доказательство

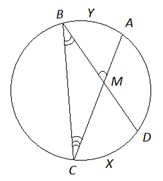Рис. 6.

Пусть хорды $A C$ и $B D$ пересекаются в точке $M$ (рис. 6).

Требуется доказать, что $∠ A M B = \frac{\overset{⏝}{C X D} + \overset{⏝}{A Y B}}{2}$ .

Угол $A M B$ – внешний угол треугольника $B M C$ . Следовательно $∠ A M B = ∠ M B C + ∠ M C B$ .

По теореме о вписанном угле $∠ M B C = \frac{\overset{⏝}{C X D}}{2}$ , $∠ M C B = \frac{\overset{⏝}{A Y B}}{2}$ .

Тогда $∠ A M B = ∠ M B C + ∠ M C B = \frac{\overset{⏝}{C X D} + \overset{⏝}{A Y B}}{2}$ .

Теорема доказана.

Теорема 4

Угол между двумя секущими, проведёнными из одной точки, равен полуразности заключённых внутри него дуг.

Доказательство

Рис. 7.

Пусть одна из секущих, проведённых из точки $M$ , пересекает окружность в точках $A$ и $B$ , а вторая секущая – в точках $C$ и $D$ (рис. 7).

Угол $B A D$ является внешним углом треугольника $A M D$ .

Поэтому

$∠ B A D = ∠ A M D + ∠ A D M \Rightarrow ∠ A M D = ∠ B A D - ∠ A D M .$

$∠ B A D = \frac{\overset{⏝}{B X D}}{2}$ , $∠ A D M = \frac{\overset{⏝}{A Y C}}{2} \Rightarrow ∠ A M D = \frac{\overset{⏝}{B X D}}{2} - \frac{\overset{⏝}{A Y C}}{2}$ .

Теорема доказана.

Сформулируем ещё две теоремы, доказательство которых аналогично доказательствам предыдущих теорем.

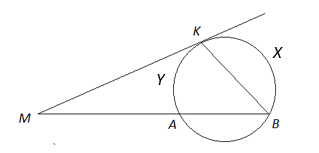Рис. 8.

Теорема 5

Угол между касательной и секущей, проведёнными из одной точки, равен полуразности заключённых внутри него дуг (рис. 8).

Применительно к рисунку 8, можно записать

$∠ M = \frac{\overset{⏝}{B X K} - \overset{⏝}{A Y K}}{2}$ .

Теорема 6

Угол между двумя касательными, проведёнными из одной точки, равен $180 °$ минус величина заключённой внутри него меньшей дуги (рис. 9).

Рис. 9.

Применительно к рисунку 9, можно записать

$∠ M = 180 ° - \overset{⏝}{A X B}$ .

Упражнение 2

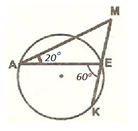Рис. 10.

Докажите теорему об угле между касательной и секущей (Теорема 5).
Докажите теорему об угле между двумя касательными (Теорема 6).
По данным, указанным на рисунке 10, найдите угол $M$ .

Контрольные вопросы

Сформулируйте теоремы об отрезках, связанных с окружностью
Сформулируйте теоремы об углах внутри и вне окружности.

Ответы

Упражнение 1

1. 3;

2. $12 \sqrt{3}$ .

Упражнение 2

3. $40 °$ .

Конспект урока: Теоремы об отрезках, связанных с окружностью. Углы с вершинами внутри и вне круга

Окружность

Теоремы об отрезках, связанных с окружностью

Углы с вершинами внутри и вне круга