Движения | Геометрия 11 класс

Движения

План урока

Центральная симметрия;
Осевая симметрия;
Зеркальная симметрия;
Параллельный перенос.

Цели урока

Знать определение движения;
Знать основные виды движений.

Разминка

Как вычислить расстояние между точками?
Какие фигуры называются равными?
Какие прямые называются параллельными?

Центральная симметрия

Определение 1

Движением называется преобразование, при котором сохраняется расстояние между точками.

При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскость – в плоскость. Можно доказать, что при движении сохраняются и углы между прямыми.

Определение 2

Центральная симметрия – это преобразование, при котором любая точка $M$ переходит в симметричную ей точку $M_{1}$ относительно данной точки $O$ . Точка $O$ при этом называется центром симметрии .

Докажем, что центральная симметрия является движением.

Пусть точка $O$ является центром симметрии. Введём прямоугольную систему координат $O x y z$ с началом в точке $O$ . При центральной симметрии с центром $O (0; 0; 0)$ , точка $M (x; y; z)$ перейдёт в симметричную ей точку $M_{1} (x_{1}; y_{1}; z_{1})$ . Если точки $M$ и $O$ не совпадают, то точка $O$ является срединой отрезка $M M_{1}$ .

По формулам координат середины отрезка, получаем

$\frac{x + x_{1}}{2} = 0$ , $\frac{y + y_{1}}{2} = 0$ , $\frac{z + z_{1}}{2} = 0$ .

Отсюда следует, что $x_{1} = - x$ , $y_{1} = - y$ , $z_{1} = - z$ .

Эти формулы верны и в случае, когда точки $M$ и $O$ совпадают (объясните самостоятельно почему). Таким образом, при центральной симметрии соответствующие координаты симметричных точек противоположны.

Рассмотрим теперь две произвольные точки $A (x_{1}; y_{1}; z_{1})$ и $B (x_{2}; y_{2}; z_{2})$ .

При центральной симметрии они перейдут соответственно в $A_{1} (- x_{1}; - y_{1}; - z_{1})$ и $B_{1} (- x_{2}; - y_{2}; - z_{2})$ . Докажем, что $A B = A_{1} B_{1}$ .

Найдем расстояния $A B$ и $A_{1} B_{1}$ .

$A B = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$

$A_{1} B_{1} = \sqrt{{(- x_{2} - (- x_{1}))}^{2} + {(- y_{2} - (- y_{1}))}^{2} + {(- z_{2} - (- z_{1}))}^{2}} =$

$= \sqrt{(- x_{2} + {x_{1}}^{2}) + {(- y_{2} + y_{1})}^{2} + {(- z_{2} + z_{1})}^{2}} = A B$ .

Таким образом, центральная симметрия является движением. Что и требовалось доказать.

Упражнение 1

1. Найдите координаты точек, в которые переходят точки $A (0; 3; 4)$ , $B (4; - 2; 5)$ , $C (2; 0; - 3)$ при центральной симметрии относительно начала координат.

2. Докажите, что при центральной симметрии:

а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую;

б) прямая, проходящая через центр симметрии, отображается на себя.

3. Докажите, что при центральной симметрии:

а) плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость;

б) плоскость, проходящая через центр симметрии, отображается на себя.

Осевая симметрия

Определение 3

Осевая симметрия с осью $a$ – это преобразование, при котором любая точка $M$ переходит в симметричную ей точку $M_{1}$ относительно оси $a$ .

Докажем, что осевая симметрия является движением .

Пусть в прямоугольной системе координат $O x y z$ ось $O z$ является осью симметрии. Тогда некоторая точка $M (x; y; z)$ перейдёт в симметричную относительно оси $O z$ точку $M_{1} (x_{1}; y_{1}; z_{1})$ . Если точка $M$ не лежит на оси $O z$ , то ось $O z$ проходит через середину отрезка $M M_{1}$ и перпендикулярна к нему. Из этого следует

$\frac{x + x_{1}}{2} = 0, \frac{y + y_{1}}{2} = 0, z_{1} = z \Rightarrow x_{1} = - x, y_{1} = - y, z_{1} = z$ .

Эти формулы верны и в случае, когда точка $M$ лежит на оси $O z$ (объясните самостоятельно почему).

Рассмотрим теперь две произвольные точки $A (x_{1}; y_{1}; z_{1})$ и $B (x_{2}; y_{2}; z_{2})$ .

При осевой симметрии они перейдут соответственно в

$A_{1} (- x_{1}; - y_{1}; z_{1})$ и $B_{1} (- x_{2}; - y_{2}; z_{2})$ . Найдем расстояния $A B$ и $A_{1} B_{1}$ .

$A B = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$

$A_{1} B_{1} = \sqrt{{(- x_{2} - (- x_{1}))}^{2} + {(- y_{2} - (- y_{1}))}^{2} + {(z_{2} - z_{1})}^{2}} =$

$= \sqrt{{(- x_{2} + x_{1})}^{2} + {(- y_{2} + y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$ .

Видим, что $A B = A_{1} B_{1}$ . Значит, осевая симметрия является движением. Что и требовалось доказать.

Упражнение 2

Найдите координаты точек, в которые переходят точки $A (0; 5; 2)$ , $B (7; - 4; 3)$ , $C (- 3; 0; - 2)$ при осевой симметрии относительно оси $O x$ .
Докажите, что при осевой симметрии прямая, параллельная оси симметрии, отображается на параллельную ей прямую.

Зеркальная симметрия

Определение 4

Зеркальной симметрией (симметрией относительно плоскости $α$ ) называется такое преобразование, при котором любая точка $M$ переходит в симметричную ей относительно плоскости $α$ точку $M_{1}$ .

Докажем, что зеркальная симметрия является движением.

Пусть в прямоугольной системе координат $O x y z$ плоскость $O x y$ является плоскостью симметрии. Тогда некоторая точка $M (x; y; z)$ перейдёт в симметричную относительно плоскости $O x y$ точку $M_{1} (x_{1}; y_{1}; z_{1})$ . Если точка $М$ не лежит в плоскости $O x y$ , то плоскость $O x y$ проходит через середину отрезка $M M_{1}$ и перпендикулярна к нему ( $M M_{1}$ параллелен оси $O z$ ). Из этого следует

$x_{1} = x, y_{1} = y, \frac{z + z_{1}}{2} = 0 \Rightarrow x_{1} = x, y_{1} = y, z_{1} = - z$ .

Полученные формулы верны и в случае, когда точка $М$ лежит в плоскости $O x y$ (объясните самостоятельно почему).

Рассмотрим теперь две произвольные точки $A (x_{1}; y_{1}; z_{1})$ и $B (x_{2}; y_{2}; z_{2})$ .

При зеркальной симметрии они перейдут соответственно в $A_{1} (x_{1}; y_{1}; - z_{1})$

и $B_{1} (x_{2}; y_{2}; - z_{2})$ . Найдем расстояния $A B$ и $A_{1} B_{1}$ .

$A B = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(z_{2} - z_{1})}^{2}}$

$A_{1} B_{1} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(- z_{2} - (- z_{1}))}^{2}} =$

$= \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2} + {(- z_{2} + z_{1})}^{2}}$ .

Получили, что $A B = A_{1} B_{1}$ . Значит, зеркальная симметрия является движением. Что и требовалось доказать.

Упражнение 3

Найдите координаты точек, в которые переходят точки $A (0; - 3; 5)$ , $B (- 7; 2; 8)$ , $C (4; 0; - 3)$ при зеркальной симметрии относительно плоскости $O y z$ .
Докажите, что при зеркальной симметрии прямая переходит в параллельную ей прямую.

Параллельный перенос

Определение 5

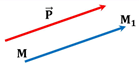Рис. 1.

Параллельным переносом на вектор $\vec{p}$ называется такое преобразование, при котором любая точка $М$ переходит в точку $M_{1}$ такую, что $\vec{M M_{1}} = \vec{p}$ (Рис. 1).

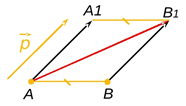Рис. 2.

Докажем, что параллельный перенос является движением .

Рассмотрим две произвольные точки $A$ и $B$ . При параллельном переносе на вектор $\vec{p}$ эти точки перейдут в точки $A_{1}$ и $B_{1}$ такие, что $\vec{A A_{1}} = \vec{p}$ , $\vec{B B_{1}} = \vec{p}$ (рис. 2).

По правилу треугольника $\vec{A B_{1}} = \vec{A A_{1}} + \vec{A_{1} B_{1}}$ и $\vec{A B_{1}} = \vec{A B} + \vec{B B_{1}}$ .

При этом $\vec{A A_{1}} = \vec{B B_{1}} \Rightarrow \vec{A_{1} B_{1}} = \vec{A B} \Rightarrow A_{1} B_{1} = A B$ . Таким образом, при параллельном переносе сохраняется между точками. Следовательно, параллельный перенос является движением. Что и требовалось доказать.

Упражнение 4

Найдите координаты точек, в которые переходят точки $A (0; - 3; 5)$ , $B (- 7; 2; 8)$ , $C (4; 0; - 3)$ при параллельном переносе на вектор $\vec{p} \{3; 4; - 2\}$ .

Контрольные вопросы

Сформулируйте определение движения.
Перечислите основные виды движений и дайте определения этих преобразований.

Ответы

Упражнение 1

1. $A_{1} (0; - 3; - 4)$ , $B_{1} (- 4; 2; - 5)$ , $C_{1} (- 2; 0; 3)$ .

Упражнение 2

1. $A_{1} (0; - 5; - 2)$ , $B_{1} (7; 4; - 3)$ , $C_{1} (- 3; 0; 2)$ .

Упражнение 3

1. $A_{1} (0; - 3; 5)$ , $B_{1} (7; 2; 8)$ , $C_{1} (- 4; 0; - 3)$ .

Упражнение 4

$A_{1} (3; 1; 3)$ , $B_{1} (- 4; 6; 6)$ , $C_{1} (7; 4; - 5)$ .

Конспект урока: Движения

Преобразования на плоскости и в пространстве

Центральная симметрия

Осевая симметрия

Зеркальная симметрия

Параллельный перенос