- Давление идеального газа
- Основное уравнение молекулярно-кинетической теории
- Среднеквадратичная скорость
- знать основное уравнение молекулярно-кинетической теории
- знать, что такое среднеквадратичная скорость
- знать взаимосвязь между давлением и средней кинетической энергией поступательного движения молекул
- Перечислите основные положения молекулярно-кинетической теории.
- Как выглядит уравнение Менделеева – Клапейрона?
- Какой процесс называют изохорным?
- Какой газ называют идеальным?
Давление идеального газа
Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда. Качественное объяснение давление газа заключается в том, что молекулы идеального газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. При столкновениях молекулы со стенкой сосуда проекция вектора скорости на ось , перпендикулярную стенке, изменяет свой знак на противоположный, но остаётся постоянной по модулю
(см. рис. 1). Поэтому в результате столкновения молекулы со стенкой проекция её импульса на ось изменяется от до .
Изменение импульса молекулы показывает, что на неё при столкновении действует сила , направленная от стенки. Изменение импульса молекулы равно импульсу силы :
.
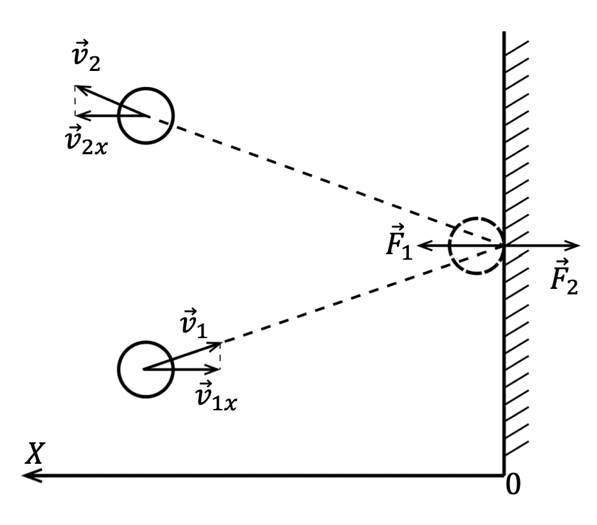 Рис. 1
Рис. 1
Во время столкновения молекула действует на стенку с силой , равной по третьему закону Ньютона силе по модулю и направленной противоположно. Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа.
Давление газа равно отношению модуля силы давления к площади стенки :
.
Основное уравнение молекулярно-кинетической теории
 Рис. 2. Движение молекулы вдоль оси X
Рис. 2. Движение молекулы вдоль оси X
Чтобы определить взаимосвязь между давлением молекул на стенки сосуда и их скоростью, рассмотрим следующую упрощённую модель. Во-первых, представим, что все молекулы газа обладают одинаковым по модулю значением скорости . Во-вторых, пусть каждая молекула газа двигается только вдоль одной из трёх координатных осей декартовой системы координат (рис. 2). Считая, что все направления движения молекул равновероятны, то по нашей моделе вдоль каждой из координатных осей будет двигаться одинаковое количество молекул. Если рассматривать, например, движение молекул на стенку вдоль положительного направления оси X, то количество приходящих молекул на стенку будет составлять 1/6 от их общего количества Чтобы лучше понять, откуда взялся коэффициент 1/6, можно представить сосуд в виде параллелепипеда, у которого 6 граней и любое движение молекул сводится к движению на одну из граней сосуда. За время до стенки площадью долетит лишь та часть молекул, которая в начальный момент времени находится на расстоянии от стенки, не превышающем значение . Таким образом, за время до стенки долетит только 1/6 часть молекул, находящихся в объёме . Значение количества приходящих на стенку молекул выразим через концентрацию .
Средняя концентрация молекул равна отношению количества молекул в рассматриваемом объёме на величину этого объёма :
, .
В конечном итоге на стенку площадью будет приходить молекул. Изменение импульса приходящих молекул вдоль оси X:
.
Таким образом, давление, вызванное силой, с которой молекулы действуют на стенку в результате упругих соударений, выглядит следующим образом:
.
На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяет вычислить давление газа, если известны масса молекулы газа, среднее значение квадрата скорости молекул и концентрация молекул .
Основное уравнение молекулярно-кинетической теории
Здесь — давление идеального газа, — масса одной молекулы,
— концентрация молекул, а величина является квадратом средней квадратичной скорости хаотического (теплового) движения молекул.
Пример 1
Какое давление на стенки сосуда оказывал бы идеальный газ с концентрацией 100 миллиардов молекул в кубическом миллиметре при средней квадратичной скорости движения молекул 1 км/с и массе молекулы 3 ∙ 10−27 кг?
Решение
1. Запишем исходные данные:
.
2. Для вычисления давления идеального газа используем основное уравнение молекулярно-кинетической теории:
.
3. Подставим значения величин и найдём давление:
.
Ответ: .
Упражнение 1
1. Считая воздух идеальным газом, оцените скорость теплового движения молекул газа при нормальных условиях (плотность воздуха при нормальных условиях равна ).
Среднеквадратичная скорость
При выводе основного уравнения молекулярно-кинетической теории было предположено, что все молекулы двигаются с одинаковой по модулю скоростью вдоль координатных осей. В реальности скорости молекул имеют различные значения, а движение происходит по всевозможным направлениям. Однако можно ввести среднее значение скорости хаотического движения молекул.
Среднеквадратичная скорость — это физическая величина, равная
,
где , … — модули скоростей всех молекул, а — их число.
Понятие скорости тесно связано с понятием кинетической энергии, поэтому введение понятия среднеквадратичной скорости позволяет записать выражение для средней кинетической энергии хаотического (теплового) поступательного движения, приходящейся на одну молекулу идеального газа:
.
Существует альтернативная запись основного уравнения молекулярно-кинетической теории через среднюю кинетическую энергию.
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объёма:
.
Пример 2
Кислород массой = 16 г при температуре = 112 °C занимает объём
= 1,6 дм3. Определите среднюю кинетическую энергию хаотического движения, приходящуюся на одну молекулу кислорода.
Решение
1. Запишем исходные данные:
.
2. Воспользуемся уравнениями Менделеева – Клапейрона и основным уравнением молекулярно-кинетической теории:
;
;
.
Приравняем правые части уравнений выше:
.
3. Из определения концентрация следует:
;
.
Запишем формулу для количества вещества:
;
.
Тогда
;
.
Ответ: .
Упражнение 2
1. В баллоне объёмом = 30 л под давлением = 200 кПа находится один моль аргона. Определите среднеквадратичную скорость хаотического движения молекул аргона, считая его идеальным газом.
Контрольные вопросы
1. Как выглядит основное уравнение молекулярно-кинетической теории?
2. Что называют среднеквадратичной скоростью?
3. Запишите основное уравнение молекулярно-кинетической теории через среднюю кинетическую энергию хаотического движения.
Упражнение 1
1. ≈ 480 м/с
Упражнение 2
1. ≈0,7 км/с
- Давление идеального газа
- Основное уравнение молекулярно-кинетической теории
- Среднеквадратичная скорость
- знать основное уравнение молекулярно-кинетической теории
- знать, что такое среднеквадратичная скорость
- знать взаимосвязь между давлением и средней кинетической энергией поступательного движения молекул
- Перечислите основные положения молекулярно-кинетической теории.
- Как выглядит уравнение Менделеева – Клапейрона?
- Какой процесс называют изохорным?
- Какой газ называют идеальным?
Давление идеального газа
Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение явления давления газа на стенки сосуда. Качественное объяснение давление газа заключается в том, что молекулы идеального газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. При столкновениях молекулы со стенкой сосуда проекция вектора скорости на ось , перпендикулярную стенке, изменяет свой знак на противоположный, но остаётся постоянной по модулю
(см. рис. 1). Поэтому в результате столкновения молекулы со стенкой проекция её импульса на ось изменяется от до .
Изменение импульса молекулы показывает, что на неё при столкновении действует сила , направленная от стенки. Изменение импульса молекулы равно импульсу силы :
.
 Рис. 1
Рис. 1
Во время столкновения молекула действует на стенку с силой , равной по третьему закону Ньютона силе по модулю и направленной противоположно. Молекул газа очень много, и удары их о стенку следуют один за другим с очень большой частотой. Среднее значение геометрической суммы сил, действующих со стороны отдельных молекул при их столкновениях со стенкой сосуда, и является силой давления газа.
Давление газа равно отношению модуля силы давления к площади стенки :
.
Основное уравнение молекулярно-кинетической теории
 Рис. 2. Движение молекулы вдоль оси X
Рис. 2. Движение молекулы вдоль оси X
Чтобы определить взаимосвязь между давлением молекул на стенки сосуда и их скоростью, рассмотрим следующую упрощённую модель. Во-первых, представим, что все молекулы газа обладают одинаковым по модулю значением скорости . Во-вторых, пусть каждая молекула газа двигается только вдоль одной из трёх координатных осей декартовой системы координат (рис. 2). Считая, что все направления движения молекул равновероятны, то по нашей моделе вдоль каждой из координатных осей будет двигаться одинаковое количество молекул. Если рассматривать, например, движение молекул на стенку вдоль положительного направления оси X, то количество приходящих молекул на стенку будет составлять 1/6 от их общего количества Чтобы лучше понять, откуда взялся коэффициент 1/6, можно представить сосуд в виде параллелепипеда, у которого 6 граней и любое движение молекул сводится к движению на одну из граней сосуда. За время до стенки площадью долетит лишь та часть молекул, которая в начальный момент времени находится на расстоянии от стенки, не превышающем значение . Таким образом, за время до стенки долетит только 1/6 часть молекул, находящихся в объёме . Значение количества приходящих на стенку молекул выразим через концентрацию .
Средняя концентрация молекул равна отношению количества молекул в рассматриваемом объёме на величину этого объёма :
, .
В конечном итоге на стенку площадью будет приходить молекул. Изменение импульса приходящих молекул вдоль оси X:
.
Таким образом, давление, вызванное силой, с которой молекулы действуют на стенку в результате упругих соударений, выглядит следующим образом:
.
На основе использования основных положений молекулярно-кинетической теории было получено уравнение, которое позволяет вычислить давление газа, если известны масса молекулы газа, среднее значение квадрата скорости молекул и концентрация молекул .
Основное уравнение молекулярно-кинетической теории
Здесь — давление идеального газа, — масса одной молекулы,
— концентрация молекул, а величина является квадратом средней квадратичной скорости хаотического (теплового) движения молекул.
Пример 1
Какое давление на стенки сосуда оказывал бы идеальный газ с концентрацией 100 миллиардов молекул в кубическом миллиметре при средней квадратичной скорости движения молекул 1 км/с и массе молекулы 3 ∙ 10−27 кг?
Решение
1. Запишем исходные данные:
.
2. Для вычисления давления идеального газа используем основное уравнение молекулярно-кинетической теории:
.
3. Подставим значения величин и найдём давление:
.
Ответ: .
Упражнение 1
1. Считая воздух идеальным газом, оцените скорость теплового движения молекул газа при нормальных условиях (плотность воздуха при нормальных условиях равна ).
Среднеквадратичная скорость
При выводе основного уравнения молекулярно-кинетической теории было предположено, что все молекулы двигаются с одинаковой по модулю скоростью вдоль координатных осей. В реальности скорости молекул имеют различные значения, а движение происходит по всевозможным направлениям. Однако можно ввести среднее значение скорости хаотического движения молекул.
Среднеквадратичная скорость — это физическая величина, равная
,
где , … — модули скоростей всех молекул, а — их число.
Понятие скорости тесно связано с понятием кинетической энергии, поэтому введение понятия среднеквадратичной скорости позволяет записать выражение для средней кинетической энергии хаотического (теплового) поступательного движения, приходящейся на одну молекулу идеального газа:
.
Существует альтернативная запись основного уравнения молекулярно-кинетической теории через среднюю кинетическую энергию.
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объёма:
.
Пример 2
Кислород массой = 16 г при температуре = 112 °C занимает объём
= 1,6 дм3. Определите среднюю кинетическую энергию хаотического движения, приходящуюся на одну молекулу кислорода.
Решение
1. Запишем исходные данные:
.
2. Воспользуемся уравнениями Менделеева – Клапейрона и основным уравнением молекулярно-кинетической теории:
;
;
.
Приравняем правые части уравнений выше:
.
3. Из определения концентрация следует:
;
.
Запишем формулу для количества вещества:
;
.
Тогда
;
.
Ответ: .
Упражнение 2
1. В баллоне объёмом = 30 л под давлением = 200 кПа находится один моль аргона. Определите среднеквадратичную скорость хаотического движения молекул аргона, считая его идеальным газом.
Контрольные вопросы
1. Как выглядит основное уравнение молекулярно-кинетической теории?
2. Что называют среднеквадратичной скоростью?
3. Запишите основное уравнение молекулярно-кинетической теории через среднюю кинетическую энергию хаотического движения.
Упражнение 1
1. ≈ 480 м/с
Упражнение 2
1. ≈0,7 км/с



