- Введение понятия логарифмической функции
- Основные свойства логарифмической функции
- Решение задач на применение свойств логарифмической функции
- Знать, что такое логарифмическая функция, ее график, основные свойства
- Уметь строить график логарифмической функции в зависимости от ее основания, применять свойства при решении задач
1.При каких значениях выражение имеет смысл:
а) ;
б) ;
в) ;
г) .
2.Найти если:
а)
б)
в)
3.Возрастающей или убывающей является функция y=f(x) на некотором промежутке, если на нем для любых выполняется
а)
б)
Логарифмической функцией называется функция вида где
Логарифмическая функция обладает следующими свойствами:
1. Область определения – множество всех положительных чисел (x>0). Следует из того, что выражение имеет смысл только при .
2. Множество значений – множество R всех действительных чисел. Следует из того, что уравнение имеет корень для любого действительного b и положительного x.
3. Функция не является ограниченной. Следует из предыдущего свойства.
4. Если a>1, то функция возрастает на промежутке ; если
0 < a < 1 , то она убывает на этом промежутке.
5. Если a > 1, то логарифмическая функция принимает положительные значения при x > 1 и отрицательные при Если 0 < a < 1, то она принимает положительные значения при а отрицательные при x > 1.
Кроме рассмотренных свойств логарифмической функции имеют место следующие утверждения, которые применяются при решении уравнений и неравенств с логарифмами:
У т в е р ж д е н и е 1. Если a > 1 и , где - положительные числа, то Если 0 < a < 1 и , где - положительные числа, то
У т в е р ж д е н и е 2. Если , где - положительные числа, то
Иными словами: если основание логарифма больше 1, то при решении неравенства с логарифмами знак неравенства сохраняется, если основание находится в промежутке (0;1), то знак неравенства меняется на противоположный.
Графики логарифмической функции в зависимости от основания функции (см. Рис.1):
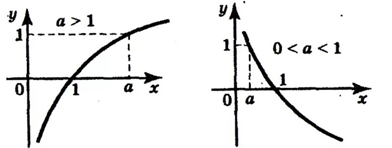 Рис. 1
Рис. 1
По графику отметим, что ось 0y является вертикальной асимптотой. Кроме того, важно запомнить, что график любой логарифмической функции проходит через точку (1; 0).
Показательная функция и логарифмическая где взаимно обратны.
Покажем это на графиках при (см. Рис. 2, Рис. 3).
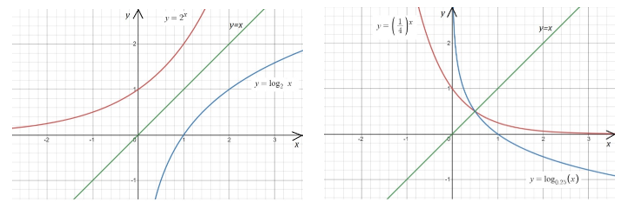 Рис. 2 Рис. 3
Рис. 2 Рис. 3
Пример 1
Выяснить, возрастающей или убывающей является функция
а) б)
Решение
а)
Основание логарифмической функции a = 3,5 > 1, значит, по свойству 4 функция возрастающая.
б)
по тому же свойству 4 функция убывающая.
Ответ: а) возрастающая; б) убывающая.
Пример 2
Сравнить числа:
a) б)
Решение
a)
Функция возрастающая, т.к. a = 7 > 0. Сравним аргументы функций: тогда (следует из определения возрастающей функции).
б)
Функция убывающая, т.к. основание логарифма находится в промежутке тогда по определению убывающей функции
Ответ: а) ; б)
Пример 3
Выяснить, положительным или отрицательным является число:
а)lg 0,2; б).
Решение
а) lg 0,2.
Основание логарифма a = 10 > 1, число, стоящее под знаком логарифмической функции По свойству 5 функция y=lg x принимает отрицательное значение при x = 0,2, значит, lg 0,2 < 0.
б) .
Согласно свойству 5 функция при x=0,7 (0 < 0,7 < 1) принимает положительные значения, значит
Ответ: а) lg 0,2 < 0; б)
Упражнение 1
Сравнить числа: а) б)
Упражнение 2
Определить знак числа: а) б)
Пример 4
Решить уравнение:
а)
б)
Решение
а)
ОДЗ:
Согласно утверждению 2: 2 – 5x = 12, x=-2. Найденный корень принадлежит ОДЗ уравнения.
Ответ: -2.
б)
ОДЗ:
Представим -2 в виде логарифма по основанию
Тогда по утверждению 2: 3x + 4 = 16, x=4. Корень принадлежит ОДЗ уравнения.
Ответ: 4.
Пример 5
Решить неравенство:
а)
б)
Решение
а)
ОДЗ: x > 0
Представим в виде логарифма по основанию 8:
Основание логарифма а = 8 > 0, тогда по утверждению 1: x < 2. После пересечения найденного множества решений с ОДЗ, получим
Ответ:
б)
ОДЗ: x > 0.
Согласно утверждению 1: После пересечения с ОДЗ получим
Ответ:
Упражнение 3
Решить уравнение
а)
б)
Упражнение 4
Решить неравенство:
а)
б)
Контрольные вопросы
1. Как связаны между собой функции:
2. Какое уравнение ассимптоты для графика функций
Упражнение 1
а) б)
Упражнение 2
а) б)
Упражнение 3
а) 17; б)
Упражнение 4
а) б)
- Введение понятия логарифмической функции
- Основные свойства логарифмической функции
- Решение задач на применение свойств логарифмической функции
- Знать, что такое логарифмическая функция, ее график, основные свойства
- Уметь строить график логарифмической функции в зависимости от ее основания, применять свойства при решении задач
1.При каких значениях выражение имеет смысл:
а) ;
б) ;
в) ;
г) .
2.Найти если:
а)
б)
в)
3.Возрастающей или убывающей является функция y=f(x) на некотором промежутке, если на нем для любых выполняется
а)
б)
Логарифмической функцией называется функция вида где
Логарифмическая функция обладает следующими свойствами:
1. Область определения – множество всех положительных чисел (x>0). Следует из того, что выражение имеет смысл только при .
2. Множество значений – множество R всех действительных чисел. Следует из того, что уравнение имеет корень для любого действительного b и положительного x.
3. Функция не является ограниченной. Следует из предыдущего свойства.
4. Если a>1, то функция возрастает на промежутке ; если
0 < a < 1 , то она убывает на этом промежутке.
5. Если a > 1, то логарифмическая функция принимает положительные значения при x > 1 и отрицательные при Если 0 < a < 1, то она принимает положительные значения при а отрицательные при x > 1.
Кроме рассмотренных свойств логарифмической функции имеют место следующие утверждения, которые применяются при решении уравнений и неравенств с логарифмами:
У т в е р ж д е н и е 1. Если a > 1 и , где - положительные числа, то Если 0 < a < 1 и , где - положительные числа, то
У т в е р ж д е н и е 2. Если , где - положительные числа, то
Иными словами: если основание логарифма больше 1, то при решении неравенства с логарифмами знак неравенства сохраняется, если основание находится в промежутке (0;1), то знак неравенства меняется на противоположный.
Графики логарифмической функции в зависимости от основания функции (см. Рис.1):
 Рис. 1
Рис. 1
По графику отметим, что ось 0y является вертикальной асимптотой. Кроме того, важно запомнить, что график любой логарифмической функции проходит через точку (1; 0).
Показательная функция и логарифмическая где взаимно обратны.
Покажем это на графиках при (см. Рис. 2, Рис. 3).
 Рис. 2 Рис. 3
Рис. 2 Рис. 3
Пример 1
Выяснить, возрастающей или убывающей является функция
а) б)
Решение
а)
Основание логарифмической функции a = 3,5 > 1, значит, по свойству 4 функция возрастающая.
б)
по тому же свойству 4 функция убывающая.
Ответ: а) возрастающая; б) убывающая.
Пример 2
Сравнить числа:
a) б)
Решение
a)
Функция возрастающая, т.к. a = 7 > 0. Сравним аргументы функций: тогда (следует из определения возрастающей функции).
б)
Функция убывающая, т.к. основание логарифма находится в промежутке тогда по определению убывающей функции
Ответ: а) ; б)
Пример 3
Выяснить, положительным или отрицательным является число:
а)lg 0,2; б).
Решение
а) lg 0,2.
Основание логарифма a = 10 > 1, число, стоящее под знаком логарифмической функции По свойству 5 функция y=lg x принимает отрицательное значение при x = 0,2, значит, lg 0,2 < 0.
б) .
Согласно свойству 5 функция при x=0,7 (0 < 0,7 < 1) принимает положительные значения, значит
Ответ: а) lg 0,2 < 0; б)
Упражнение 1
Сравнить числа: а) б)
Упражнение 2
Определить знак числа: а) б)
Пример 4
Решить уравнение:
а)
б)
Решение
а)
ОДЗ:
Согласно утверждению 2: 2 – 5x = 12, x=-2. Найденный корень принадлежит ОДЗ уравнения.
Ответ: -2.
б)
ОДЗ:
Представим -2 в виде логарифма по основанию
Тогда по утверждению 2: 3x + 4 = 16, x=4. Корень принадлежит ОДЗ уравнения.
Ответ: 4.
Пример 5
Решить неравенство:
а)
б)
Решение
а)
ОДЗ: x > 0
Представим в виде логарифма по основанию 8:
Основание логарифма а = 8 > 0, тогда по утверждению 1: x < 2. После пересечения найденного множества решений с ОДЗ, получим
Ответ:
б)
ОДЗ: x > 0.
Согласно утверждению 1: После пересечения с ОДЗ получим
Ответ:
Упражнение 3
Решить уравнение
а)
б)
Упражнение 4
Решить неравенство:
а)
б)
Контрольные вопросы
1. Как связаны между собой функции:
2. Какое уравнение ассимптоты для графика функций
Упражнение 1
а) б)
Упражнение 2
а) б)
Упражнение 3
а) 17; б)
Упражнение 4
а) б)



