- Введение понятия обратимой функции
- Введение понятия функции, обратной данной, взаимно обратных функций
- Решение задач на нахождение функций, обратных данным
- Формулировка теорем об обратимости монотонной функции, симметричности графиков взаимно обратных функций
- Знать определение обратимой функции, функции обратной для данной функции, теорем об обратных функциях
- Уметь строить графики функций, обратных данным
1. Назовите промежутки возрастания и убывания функций:
а) ;
б) ;
в) ;
г) .
2. Выразите из формулы:
а) переменную R из ;
б) переменную R из ;
в) переменную h из .
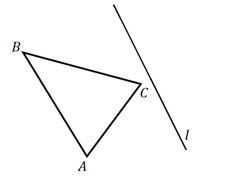
3. Как выполняется осевая симметрия? Постройте фигуру, симметричную треугольнику ABC, относительно прямой l.
Пусть есть некоторая функция , заданная на некотором множестве D. Для каждого значения аргумента из множества D можно найти соответствующее значение функции, и, наоборот, для каждого значения y можно найти соответствующее значение x.
Если функция f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
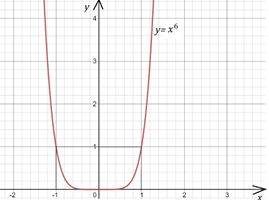 Рис. 1
Рис. 1
Например, функция при и принимает значение , значит, она не является обратимой (см. рис. 1).
А функция каждое свое значение y принимает при единственном значении x (см. рис. 2), она является обратимой.
Пусть дана обратимая функция f(x). Согласно определению, данному выше, каждому значению функции y из множества значений функции E(f) соответствует только одно значение аргумента x из области определения функции D(f), что . Это соответствие определяет функцию x от y, обозначим ее . Перейдя к привычному обозначению, поменяв местами x и y, получим , функцию, обратную для f(x).
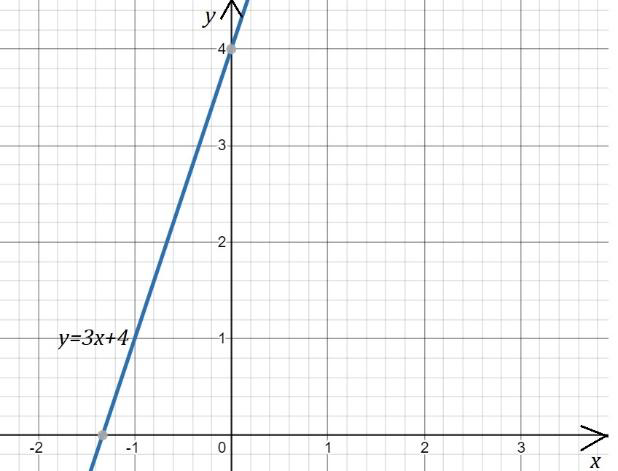 Рис. 2
Рис. 2
Если обратимая функция f(x) задана формулой, то для того, чтобы найти обратную ей функцию, нужно решить уравнение относительно переменной x и поменять местами переменные x и y. Эти функции называют взаимно обратными.
Из определения обратной функции следует, что область определения обратной функции такая же как и множество значений исходной функции, множество значений обратной – область определения исходной.
Пример 1
Найти функции, обратные к данным:
а) ;
б) .
Решение
а) .
Решим это уравнение относительно x, получим . Меняем местами переменные x и y, получаем формулу для функции, обратной данной, а именно .
б)
Заменив x на y и y на x, имеем .
Ответ: а) ; б) .
Упражнение 1
Найти функции, обратные к данным:
а) ;
б) .
Возрастающие и убывающие функции называются монотонными функциями.
Теорема 1
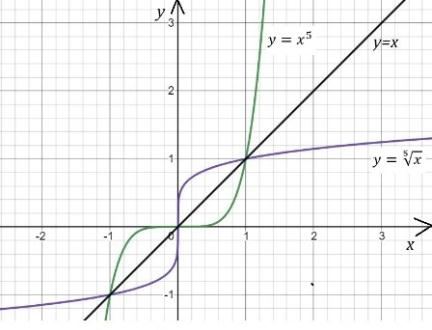 Рис. 3
Рис. 3
Монотонная функция является обратимой.
Например, функция является возрастающей, тогда по теореме 1, она будет обратимой. Обратная для нее функция (см. рис. 3).
Какой характер монотонности у исходной функции, такой же будет и у обратной, т.е. если исходная функция возрастает, то и обратная будет возрастать; если убывала, то обратная тоже убывает.
Теорема 2
Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой . (См. пример на рис. 3).
Пусть дана функция . Так как эта функция монотонна, то по теореме 1 она обратима. Обратной ей функцией будет .
Пример 2
На одном рисунке построить графики данной функции и функции, обратной к ней. Указать область определения исходной и множество значений обратной функций.
а) ;
б) .
Решение
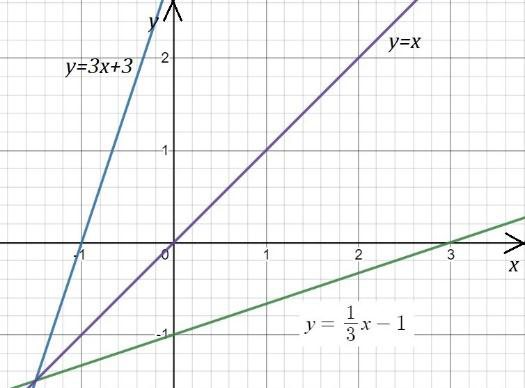 Рис. 4
Рис. 4
а)
Строим график функции и симметричный ему относительно график обратной функции. Чтобы найти формулу для обратной функции, решим уравнение относительно x, затем поменяем переменные местами. Получим (см. рис. 4).
Область определения исходной функции – вся числовая прямая, таким же будет и множество значений для обратной функции .
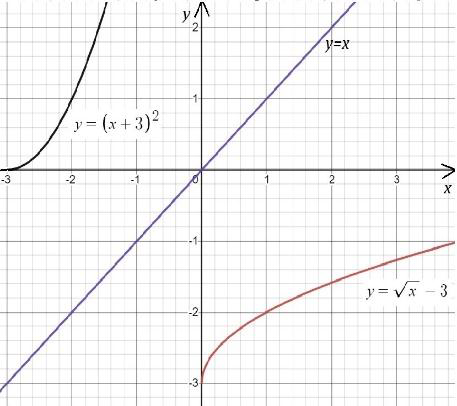 Рис. 5
Рис. 5
б)
Для отыскания обратной функции выразим x через y, поменяем местами переменные: .
Область определения исходной: , множество значений обратной - (см. рис. 5).
Упражнение 2
На одном рисунке построить графики данной функции и функции, обратной к ней. Указать область определения исходной и множество значений обратной функций.
а) ;
б) .
Итак:
- Если функция f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
- Для нахождения функции, обратной для , нужно решить это уравнение относительно x и поменять местами x и y. Если уравнение имеет более одного корня, то функции, обратной данной, не существует.
- Графики взаимно обратных функций симметричны относительно прямой .
Контрольные вопросы
- Объясните, что такое монотонная функция. Приведите примеры.
- Объясните, что такое обратимая функция. Приведите примеры. Приведите пример функции, которая не является обратимой.
- Объясните, что такое взаимно обратные функции. Приведите примеры.
Упражнение 1
а) ; б) .
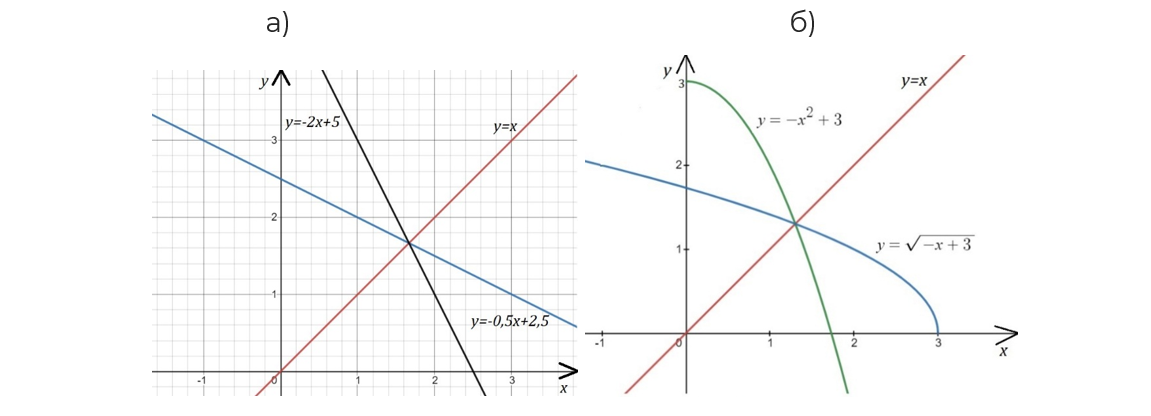
Упражнение 2
- Введение понятия обратимой функции
- Введение понятия функции, обратной данной, взаимно обратных функций
- Решение задач на нахождение функций, обратных данным
- Формулировка теорем об обратимости монотонной функции, симметричности графиков взаимно обратных функций
- Знать определение обратимой функции, функции обратной для данной функции, теорем об обратных функциях
- Уметь строить графики функций, обратных данным
1. Назовите промежутки возрастания и убывания функций:
а) ;
б) ;
в) ;
г) .
2. Выразите из формулы:
а) переменную R из ;
б) переменную R из ;
в) переменную h из .

3. Как выполняется осевая симметрия? Постройте фигуру, симметричную треугольнику ABC, относительно прямой l.
Пусть есть некоторая функция , заданная на некотором множестве D. Для каждого значения аргумента из множества D можно найти соответствующее значение функции, и, наоборот, для каждого значения y можно найти соответствующее значение x.
Если функция f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
 Рис. 1
Рис. 1
Например, функция при и принимает значение , значит, она не является обратимой (см. рис. 1).
А функция каждое свое значение y принимает при единственном значении x (см. рис. 2), она является обратимой.
Пусть дана обратимая функция f(x). Согласно определению, данному выше, каждому значению функции y из множества значений функции E(f) соответствует только одно значение аргумента x из области определения функции D(f), что . Это соответствие определяет функцию x от y, обозначим ее . Перейдя к привычному обозначению, поменяв местами x и y, получим , функцию, обратную для f(x).
 Рис. 2
Рис. 2
Если обратимая функция f(x) задана формулой, то для того, чтобы найти обратную ей функцию, нужно решить уравнение относительно переменной x и поменять местами переменные x и y. Эти функции называют взаимно обратными.
Из определения обратной функции следует, что область определения обратной функции такая же как и множество значений исходной функции, множество значений обратной – область определения исходной.
Пример 1
Найти функции, обратные к данным:
а) ;
б) .
Решение
а) .
Решим это уравнение относительно x, получим . Меняем местами переменные x и y, получаем формулу для функции, обратной данной, а именно .
б)
Заменив x на y и y на x, имеем .
Ответ: а) ; б) .
Упражнение 1
Найти функции, обратные к данным:
а) ;
б) .
Возрастающие и убывающие функции называются монотонными функциями.
Теорема 1
 Рис. 3
Рис. 3
Монотонная функция является обратимой.
Например, функция является возрастающей, тогда по теореме 1, она будет обратимой. Обратная для нее функция (см. рис. 3).
Какой характер монотонности у исходной функции, такой же будет и у обратной, т.е. если исходная функция возрастает, то и обратная будет возрастать; если убывала, то обратная тоже убывает.
Теорема 2
Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой . (См. пример на рис. 3).
Пусть дана функция . Так как эта функция монотонна, то по теореме 1 она обратима. Обратной ей функцией будет .
Пример 2
На одном рисунке построить графики данной функции и функции, обратной к ней. Указать область определения исходной и множество значений обратной функций.
а) ;
б) .
Решение
 Рис. 4
Рис. 4
а)
Строим график функции и симметричный ему относительно график обратной функции. Чтобы найти формулу для обратной функции, решим уравнение относительно x, затем поменяем переменные местами. Получим (см. рис. 4).
Область определения исходной функции – вся числовая прямая, таким же будет и множество значений для обратной функции .
 Рис. 5
Рис. 5
б)
Для отыскания обратной функции выразим x через y, поменяем местами переменные: .
Область определения исходной: , множество значений обратной - (см. рис. 5).
Упражнение 2
На одном рисунке построить графики данной функции и функции, обратной к ней. Указать область определения исходной и множество значений обратной функций.
а) ;
б) .
Итак:
- Если функция f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
- Для нахождения функции, обратной для , нужно решить это уравнение относительно x и поменять местами x и y. Если уравнение имеет более одного корня, то функции, обратной данной, не существует.
- Графики взаимно обратных функций симметричны относительно прямой .
Контрольные вопросы
- Объясните, что такое монотонная функция. Приведите примеры.
- Объясните, что такое обратимая функция. Приведите примеры. Приведите пример функции, которая не является обратимой.
- Объясните, что такое взаимно обратные функции. Приведите примеры.
Упражнение 1
а) ; б) .
Упражнение 2




