- Введение понятия показательной функции
- Формулировка свойств показательной функции
- Графики показательной функции в зависимости от основания степени а
- Решение задач с помощью графиков и свойств показательной функции
- Знать определение показательной функции, ее свойства.
- Уметь строить по точкам графики конкретных показательных функций, строить эскизы графика показательной функции в зависимости от основания степени а, использовать свойства показательной функции при решении задач
1. Представьте в виде степени числа :
а) ; б) ; в) .
2. Сравнить с единицей:
а) ; б) .
3. С помощью графика (см. рис. 1) найдите:
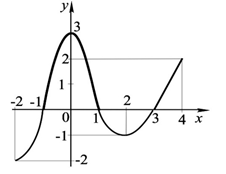 Рис. 1
Рис. 1
1) значения аргумента, при которых функция принимает положительные значения, отрицательные значения;
2) значения аргумента, при которых значение функции равно нулю;
3) промежутки возрастания, убывания функции;
4) координаты точек пересечения с осями координат.
Вспомним свойства степени с действительным показателем.
Пусть . Тогда
- если
- если
- если
- ;
- ;
- ;
- ;
- .
На практике мы часто сталкиваемся с функциями вида , например, .
Такие функции называются показательными, где неизвестное – показатель степени.
Показательной функцией называется функция вида , – заданное действительное число, .
Свойства показательной функции
- Область определения – множество R всех действительных чисел.
- Множество значений – множество всех положительных чисел.
- Показательная функция является возрастающей на множестве всех действительных чисел, если , и убывающей, если .
График показательной функции в зависимости от основания степени a (рис. 2):
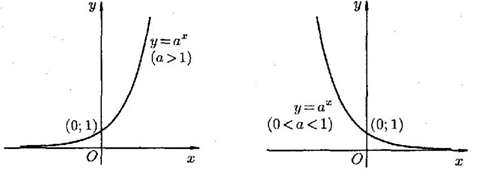 Рис. 2
Рис. 2
Пример 1
С помощью графика функции найти приближенное значение числа:
а) ; б) ; в) .
Решение
Построим по точкам график функции (рис. 3).
|
x
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
y
|
|
|
|
1
|
2
|
4
|
8
|
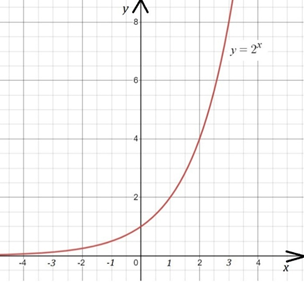 Рис. 3
Рис. 3
|
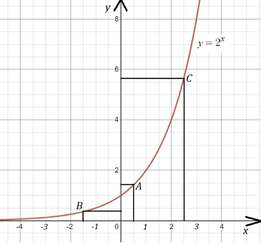 Рис. 4
Рис. 4
|
а) . Найдем значение функции при : (ордината точки А на рис. 4).
б) (ордината точки В на рис. 4).
в) (ордината точки С на рис. 4).
Ответ: а) б) в)
Упражнение 1
С помощью графика функции найти приближенное значение числа:
а) ; б) .
Пример 2
Выяснить, возрастающей или убывающей является функция:
а) ; б) ; в) .
Решение
а) . Так как , то функция возрастающая.
б) . , значит, функция убывающая.
в) . Так как , то функция убывающая.
Ответ: а) возрастающая; б) убывающая; в) убывающая.
Упражнение 2
Выяснить, возрастающей или убывающей является функция:
а) ; б) ; в) .
Пример 3
Сравнить с единицей.
Решение
Представим единицу в виде . Основание степени , значит, функция убывающая. Так как , то , т.е. .
Ответ: .
Упражнение 3
Сравнить числа:
а) ; б) ; в)
Пример 4
Решить графически уравнение .
Решение
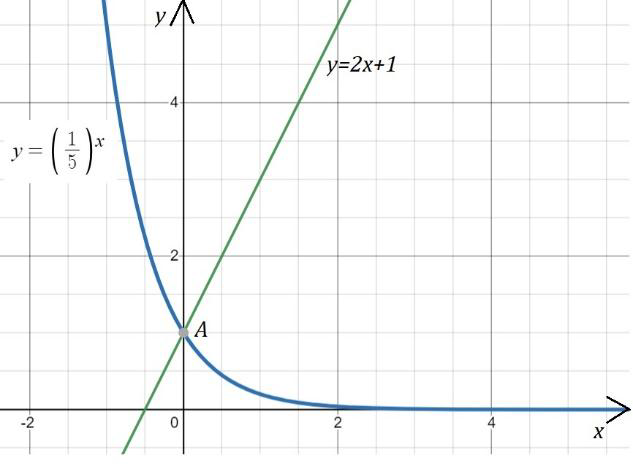 Рис. 5
Рис. 5
В одной и той же системе координат построим графики функций и .
Графики функций пересекаются в точке А(0;1). Абсцисса этой точки x=0 и будет решением исходного уравнения.
Ответ: 0.
Упражнение 4
Пользуясь графиком, определите количество корней уравнения .
Итак:
- Показательная функция – функция вида .
- Свойства показательной функции :
- Область определения – множество всех действительных чисел ().
- Область значений – множество всех положительных чисел ().
- График функции проходит через точку (0;1).
- Функция возрастающая при , функция убывающая при .
Контрольные вопросы
- Приведите пример показательной функции.
- Является ли функция показательной? Почему?
Упражнение 1
а) ; б) .
Упражнение 2
а) возрастающая; б) возрастающая; в) убывающая.
Упражнение 3
а) ; б) ; в) .
Упражнение 4
Два корня.
- Введение понятия показательной функции
- Формулировка свойств показательной функции
- Графики показательной функции в зависимости от основания степени а
- Решение задач с помощью графиков и свойств показательной функции
- Знать определение показательной функции, ее свойства.
- Уметь строить по точкам графики конкретных показательных функций, строить эскизы графика показательной функции в зависимости от основания степени а, использовать свойства показательной функции при решении задач
1. Представьте в виде степени числа :
а) ; б) ; в) .
2. Сравнить с единицей:
а) ; б) .
3. С помощью графика (см. рис. 1) найдите:
 Рис. 1
Рис. 1
1) значения аргумента, при которых функция принимает положительные значения, отрицательные значения;
2) значения аргумента, при которых значение функции равно нулю;
3) промежутки возрастания, убывания функции;
4) координаты точек пересечения с осями координат.
Вспомним свойства степени с действительным показателем.
Пусть . Тогда
- если
- если
- если
- ;
- ;
- ;
- ;
- .
На практике мы часто сталкиваемся с функциями вида , например, .
Такие функции называются показательными, где неизвестное – показатель степени.
Показательной функцией называется функция вида , – заданное действительное число, .
Свойства показательной функции
- Область определения – множество R всех действительных чисел.
- Множество значений – множество всех положительных чисел.
- Показательная функция является возрастающей на множестве всех действительных чисел, если , и убывающей, если .
График показательной функции в зависимости от основания степени a (рис. 2):
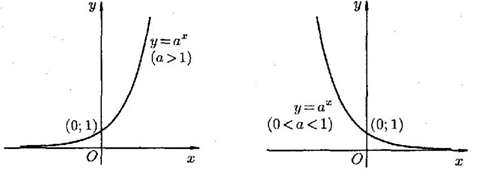 Рис. 2
Рис. 2
Пример 1
С помощью графика функции найти приближенное значение числа:
а) ; б) ; в) .
Решение
Построим по точкам график функции (рис. 3).
|
x
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
|
y
|
|
|
|
1
|
2
|
4
|
8
|
 Рис. 3
Рис. 3
|
 Рис. 4
Рис. 4
|
а) . Найдем значение функции при : (ордината точки А на рис. 4).
б) (ордината точки В на рис. 4).
в) (ордината точки С на рис. 4).
Ответ: а) б) в)
Упражнение 1
С помощью графика функции найти приближенное значение числа:
а) ; б) .
Пример 2
Выяснить, возрастающей или убывающей является функция:
а) ; б) ; в) .
Решение
а) . Так как , то функция возрастающая.
б) . , значит, функция убывающая.
в) . Так как , то функция убывающая.
Ответ: а) возрастающая; б) убывающая; в) убывающая.
Упражнение 2
Выяснить, возрастающей или убывающей является функция:
а) ; б) ; в) .
Пример 3
Сравнить с единицей.
Решение
Представим единицу в виде . Основание степени , значит, функция убывающая. Так как , то , т.е. .
Ответ: .
Упражнение 3
Сравнить числа:
а) ; б) ; в)
Пример 4
Решить графически уравнение .
Решение
 Рис. 5
Рис. 5
В одной и той же системе координат построим графики функций и .
Графики функций пересекаются в точке А(0;1). Абсцисса этой точки x=0 и будет решением исходного уравнения.
Ответ: 0.
Упражнение 4
Пользуясь графиком, определите количество корней уравнения .
Итак:
- Показательная функция – функция вида .
- Свойства показательной функции :
- Область определения – множество всех действительных чисел ().
- Область значений – множество всех положительных чисел ().
- График функции проходит через точку (0;1).
- Функция возрастающая при , функция убывающая при .
Контрольные вопросы
- Приведите пример показательной функции.
- Является ли функция показательной? Почему?
Упражнение 1
а) ; б) .
Упражнение 2
а) возрастающая; б) возрастающая; в) убывающая.
Упражнение 3
а) ; б) ; в) .
Упражнение 4
Два корня.



