- Введение понятия степенной функции
- Ограниченная функция
- Свойства степенной функции в зависимости от показателя степени
- Решение задач на применение свойств степенной функции
- Знать виды графиков степенной функции в зависимости от показателя степени, их свойства
- Уметь использовать свойства степенной функции при решении задач
С помощью графиков функций ответьте на вопросы:
- Какая область определения функции ?
- Какое множество значений функции ?
- Является ли функция четной? Нечетной?
- Найти промежутки возрастания, убывания функции.
- При каких значениях x функция принимает положительные значения? Отрицательные значения? Значение, равное 0?
- Найти значение функции при .
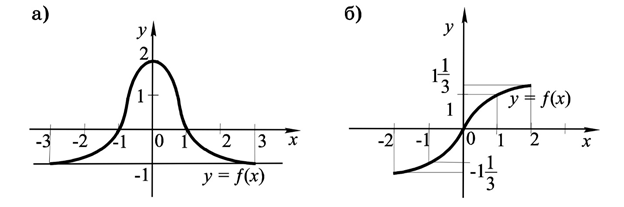 Рис. 1
Рис. 1
Начиная с 7 класса, вы знакомились с различными видами функций:
и т.д. Все перечисленные функции являются частными случаями функции , которая называется степенной. Ее свойства зависят от свойств степени с действительным показателем, от того, при каких x, p имеет смысл .
Функция , определенная на множество Х, называется ограниченной снизу на множестве Х, если существует такое число С1, что для любого выполняется неравенство .
Можно сказать, что все точки графика функции находятся выше прямой или на этой прямой (см. рис. 2, а).
Функция , определенная на множество Х, называется ограниченной сверху на множестве Х, если существует такое число С2, что для любого выполняется неравенство .
В этом случае все точки графика функции находятся ниже прямой или на этой прямой (см. рис. 2, б).
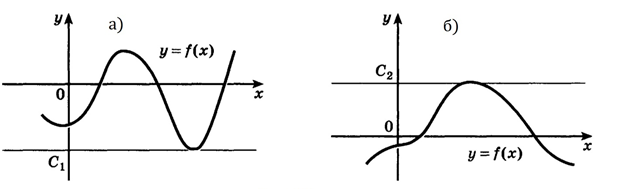 Рис. 2
Рис. 2
Примерами функций, ограниченной снизу могут быть функции , ограниченной сверху - .
Функция , определенная на множестве Х, называется ограниченной на множестве Х, если она ограничена и сверху, и снизу, или, другими словами, когда существует такое число С, что для любого выполняется неравенство
Пример ограниченных функций
Рассмотрим свойства степенной функции в зависимости от показателя степени p.
Таблица 1. Свойства степенной функции

Пример 1
Найти наибольшее и наименьшее значения функции на отрезке .
Решение
Функция возрастает на всей своей области определения R, тогда наибольшее значение на отрезке она достигает в точке , а наименьшее в .
Ответ: .
Пример 2
Среди функций выбрать ту, у которой множеством значений является множество всех действительных чисел кроме нуля.
Решение
У функции множеством значений является множество всех действительных чисел кроме нуля, т.к. – целое, нечетное.
Ответ: .
Пример 3
Какая из функций или возрастает на отрезке ?
Решение
Отрезок принадлежит лучу . Функция убывает в каждой точке этого луча, т.к. степень отрицательная, четная. Функция с положительной нечетной степенью возрастает везде на , значит, и на отрезке .
Ответ: .
Упражнение 1
Найти наибольшее и наименьшее значения функции на отрезке .
Упражнение 2
Найти область определения функций:
а)
б)
Упражнение 3
Какая из функций или возрастает на отрезке ?
Итак:
- Функция вида называется степенной функцией.
2. Свойства степенной функции в зависимости от показателя степени можно увидеть в таблице.
Контрольные вопросы
- Какие из функций убывают, какие возрастают: ?
- Приведите пример функции, ограниченной снизу, ограниченной сверху.
Упражнение 1
Упражнение 2
а) ; б) .
Упражнение 3
- Введение понятия степенной функции
- Ограниченная функция
- Свойства степенной функции в зависимости от показателя степени
- Решение задач на применение свойств степенной функции
- Знать виды графиков степенной функции в зависимости от показателя степени, их свойства
- Уметь использовать свойства степенной функции при решении задач
С помощью графиков функций ответьте на вопросы:
- Какая область определения функции ?
- Какое множество значений функции ?
- Является ли функция четной? Нечетной?
- Найти промежутки возрастания, убывания функции.
- При каких значениях x функция принимает положительные значения? Отрицательные значения? Значение, равное 0?
- Найти значение функции при .
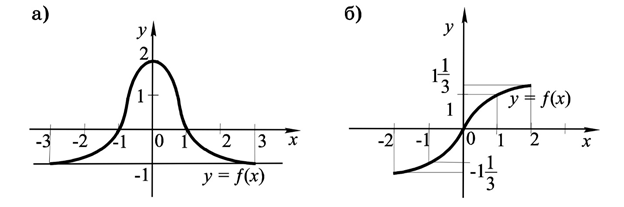 Рис. 1
Рис. 1
Начиная с 7 класса, вы знакомились с различными видами функций:
и т.д. Все перечисленные функции являются частными случаями функции , которая называется степенной. Ее свойства зависят от свойств степени с действительным показателем, от того, при каких x, p имеет смысл .
Функция , определенная на множество Х, называется ограниченной снизу на множестве Х, если существует такое число С1, что для любого выполняется неравенство .
Можно сказать, что все точки графика функции находятся выше прямой или на этой прямой (см. рис. 2, а).
Функция , определенная на множество Х, называется ограниченной сверху на множестве Х, если существует такое число С2, что для любого выполняется неравенство .
В этом случае все точки графика функции находятся ниже прямой или на этой прямой (см. рис. 2, б).
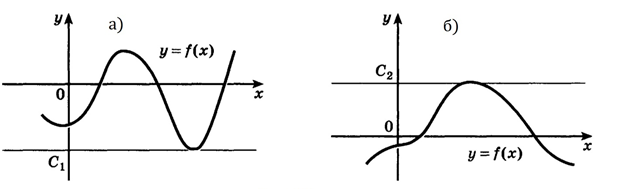 Рис. 2
Рис. 2
Примерами функций, ограниченной снизу могут быть функции , ограниченной сверху - .
Функция , определенная на множестве Х, называется ограниченной на множестве Х, если она ограничена и сверху, и снизу, или, другими словами, когда существует такое число С, что для любого выполняется неравенство
Пример ограниченных функций
Рассмотрим свойства степенной функции в зависимости от показателя степени p.
Таблица 1. Свойства степенной функции

Пример 1
Найти наибольшее и наименьшее значения функции на отрезке .
Решение
Функция возрастает на всей своей области определения R, тогда наибольшее значение на отрезке она достигает в точке , а наименьшее в .
Ответ: .
Пример 2
Среди функций выбрать ту, у которой множеством значений является множество всех действительных чисел кроме нуля.
Решение
У функции множеством значений является множество всех действительных чисел кроме нуля, т.к. – целое, нечетное.
Ответ: .
Пример 3
Какая из функций или возрастает на отрезке ?
Решение
Отрезок принадлежит лучу . Функция убывает в каждой точке этого луча, т.к. степень отрицательная, четная. Функция с положительной нечетной степенью возрастает везде на , значит, и на отрезке .
Ответ: .
Упражнение 1
Найти наибольшее и наименьшее значения функции на отрезке .
Упражнение 2
Найти область определения функций:
а)
б)
Упражнение 3
Какая из функций или возрастает на отрезке ?
Итак:
- Функция вида называется степенной функцией.
2. Свойства степенной функции в зависимости от показателя степени можно увидеть в таблице.
Контрольные вопросы
- Какие из функций убывают, какие возрастают: ?
- Приведите пример функции, ограниченной снизу, ограниченной сверху.
Упражнение 1
Упражнение 2
а) ; б) .
Упражнение 3



