Конспект урока: Системы неравенств с двумя переменными

Решение системы неравенств с двумя переменными

Неравенство с двумя переменными можно решить графически, изобразив область решения на координатной плоскости. Аналогично можно решить и систему неравенств. 

Решение одного неравенства с двумя переменными тесно связано с графическим изображением решения уравнения с двумя переменными. Значит, и решение системы неравенств тесно связано с решением соответствующей системы уравнений.

Вспомним, что систему уравнений с двумя переменными можно решить несколькими способами, один из которых графический. Для этого необходимо построить график каждого уравнения и определить координаты их точек пересечения. Это и будет решение системы уравнений с двумя переменными.

Решение системы неравенств с двумя переменными будет определяться аналогичным образом. Но сначала определим, что будем называть решением системы неравенств с двумя переменными.

Алгоритм решения системы неравенств графическим способом

Графический метод решения системы неравенств с двумя переменными является единственным способом решения, изучаемым в школе. Его главное достоинство состоит в том, что этот способ является наглядным. 

Определим алгоритм решения наших систем.

Изобразить множество решений системы $\left\{\begin{array}{l}x+y>0,\\ y+x^2\le 5.\end{array}\right.$

Решение

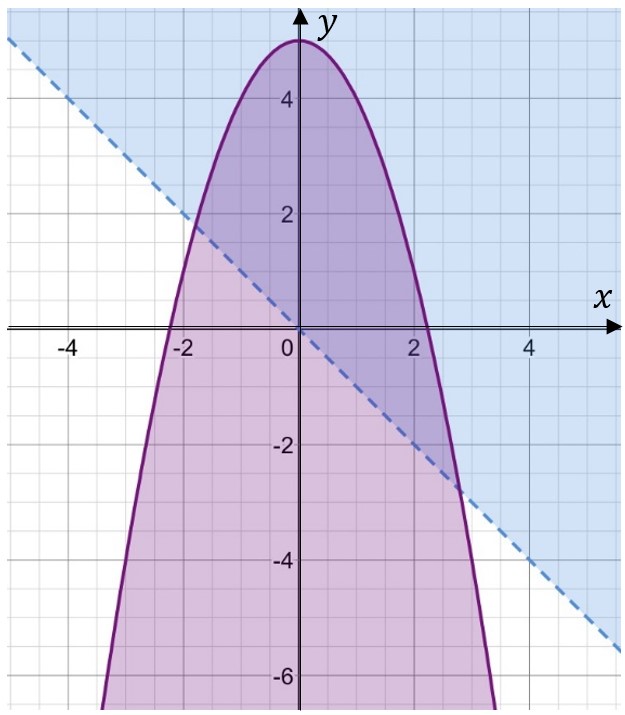Рис. 1. Решение системы 1

Решением неравенства $x+y>0$ является область выше прямой $y=-x$ причём прямая изображена пунктиром, т. к. неравенство строгое (на рис. 1 — голубая область).

 

Решение второго неравенства $y+x^2\le 5$ — область внутри параболы $y=5-x^2$, включая саму параболу, т. к. неравенство нестрогое и граница параболы изображена сплошной линией (на рис. 1 — фиолетовая область).

 

Пересечение голубой и фиолетовой 
областей — решение системы неравенств $\left\{\begin{array}{l}x+y>0,\\ y+x^2\le 5.\end{array}\right.$

Можно сделать вывод, что графический способ даёт лишь наглядное представление о решении системы неравенств с двумя переменными. Решение системы является областью, границы которой — графики соответствующих уравнений с двумя переменными.

Изобразить множество решений системы $\left\{\begin{array}{l}xy>2,\\ x^2+y^2<25.\end{array}\right.$

Решение

Рис. 2. Решение системы 2

Решением неравенства $xy>2$ является область вне ветвей гиперболы $xy=2,$ причем гипербола изображена пунктиром, т.к. неравенство строгое (на рис. 2 — зеленая область).

 

Решение второго неравенства $x^2+y^2<25$ — область внутри окружности $x^2+y^2=25$, не включая саму окружность, т.к. неравенство строгое и окружность изображена пунктиром (на рис. 2 — голубая область).

 

Пересечение голубой и зеленой областей — решение системы неравенств $\left\{\begin{array}{l}xy>2,\\ x^2+y^2<25.\end{array}\right.$

1. Изобразить множество решений системы $\left\{\begin{array}{l}x+2y<4,\\ 2x-y>3.\end{array}\right.$

2. Изобразить множество решений системы $\left\{\begin{array}{l}y-x^2-2x+3>0,\\ y+2x<0.\end{array}\right.$

1. Может ли система неравенств с двумя переменными не иметь решений? Ответ поясните.

2. Как найти, какие точно значения могут принимать переменные $x$ и $y$, являющиеся решениями?

Упражнение 1

1. 

2.