Функция корня и её график

Функция

\sqrt{x}

и ее график

План урока

Функция $y = \sqrt{x}$ и ее график
Симметрия графиков функций $y = x^{2}$ (при $x \geq 0$ ) и $y = \sqrt{x}$
Графическое решение уравнений вида $\sqrt{x} = k x + b$

Цели урока

Уметь строить график функции $y = \sqrt{x}$
Знать свойства функции $y = \sqrt{x}$
Уметь сравнивать действительные числа с помощью свойств функции $y = \sqrt{x}$
Знать свойство симметричности графиков функций $y = x^{2}$ (при $x \geq 0$ ) и $y = \sqrt{x}$
Уметь решать уравнения вида $\sqrt{x} = k x + b$ графическим способом

Разминка

Решите уравнение:

а) $x^{2} = 169$ ; б) $x^{2} = 3$ ; в) $\sqrt{x} = 3$ ; г) $\sqrt{x} - 2 = 9$

Функция $y = \sqrt{x}$ и ее график

Пусть длина стороны квадрата равна a см, а его площадь равна S см². Каждому значению длины a стороны квадрата соответствует единственное значение его площади S. Зависимость площади квадрата от длины его стороны выражается формулой S = a², где $a \geq 0$ .

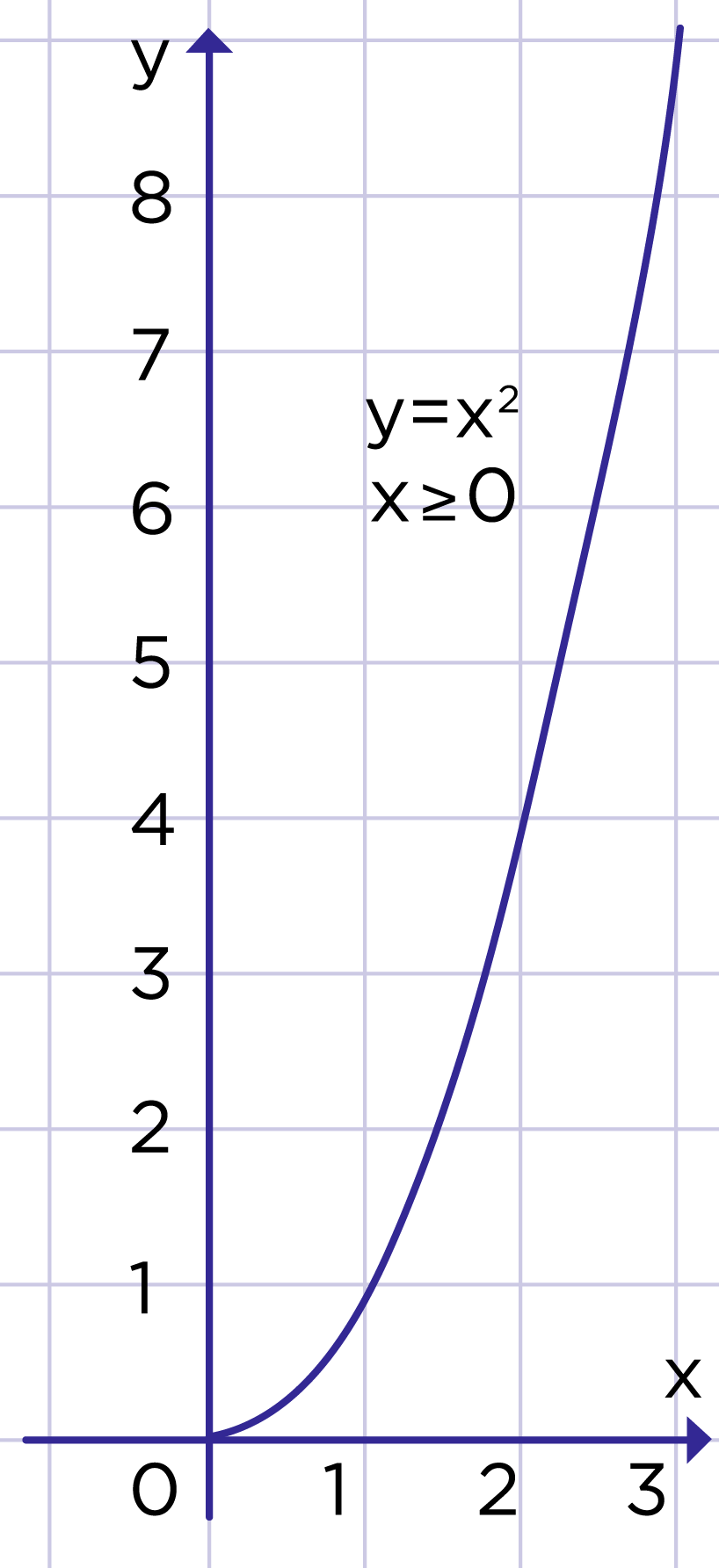Рис. 1. График функции

И, наоборот, каждому значению площади квадрата S соответствует единственное значение длины стороны a. Зависимость длины стороны квадрата от площади выражается формулой $a = \sqrt{S}$ .

Формулы S = a², где $a \geq 0$ , и $a = \sqrt{S}$ выражают функциональные зависимости между переменными a и S. Только в первом случае независимой переменной является длина a стороны квадрата, а во втором — площадь S.

Если независимую переменную обозначить буквой x, а зависимую переменную – y, то получим формулы

$y = x^{2}$ , где $x \geq 0$ , и $y = \sqrt{x}$ .

Графиком функции $y = x^{2}$ , где $x \geq 0$ , является правая ветвь параболы (рис. 1). Построим далее график функции $y = \sqrt{x}$ .

Т.к. выражение $\sqrt{x}$ имеет смысл при неотрицательных значениях x, то областью определения функции служит множество неотрицательных чисел.

Составим таблицу значений функции $y = \sqrt{x}$ (для значений x, не являющихся квадратами целых чисел посчитаем приближенные значения y с точностью до 0,1):

x	0	0,5	1	2	3	4	5	6	7	8	9
y	0	0,7	1	1,4	1,7	2	2,2	2,4	2,6	2,8	3

Построим в координатной плоскости точки, координаты которых указаны в таблице. Проведем от начала координат плавную линию и получим график функции $y = \sqrt{x}$ .

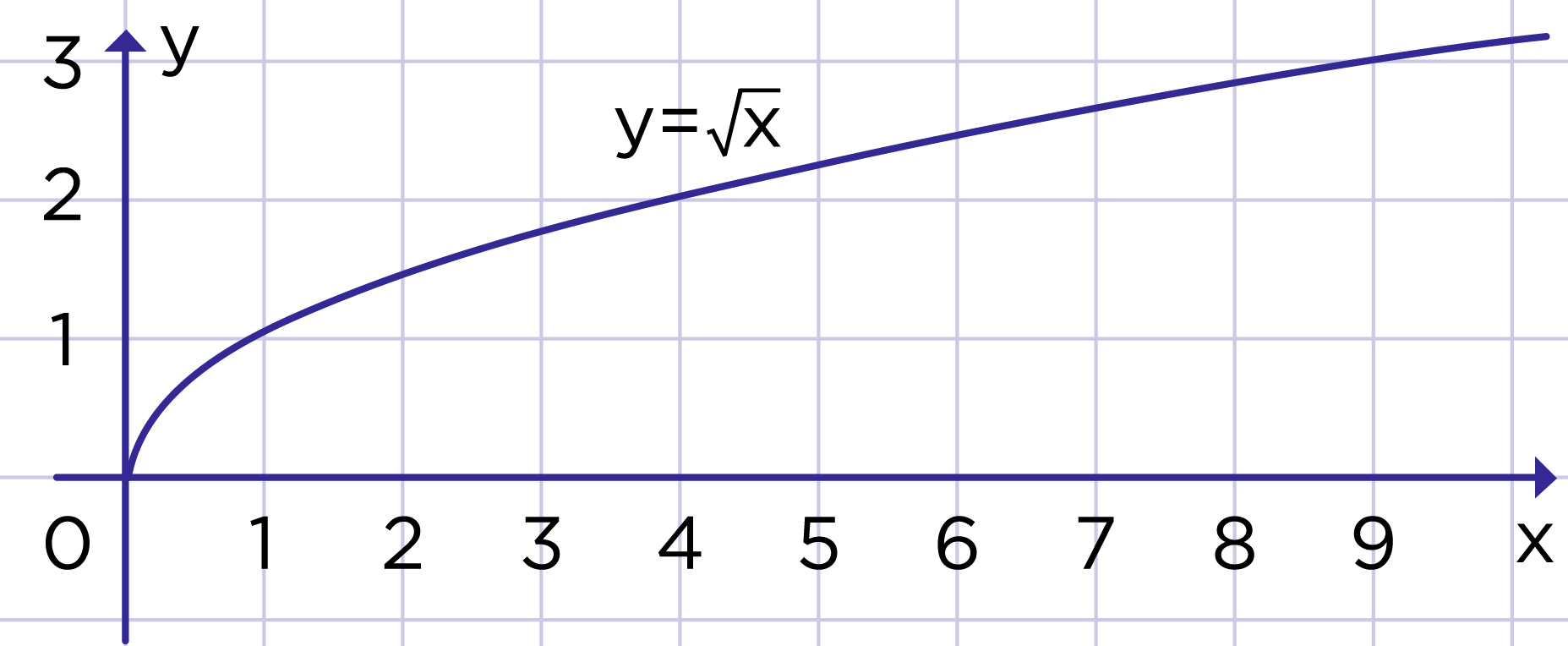
^{Рис. 2. График функции} $y = \sqrt{x}$

Перечислим некоторые свойства функции $y = \sqrt{x}$ (рис. 2).

1. Если x = 0, то y = 0, поэтому начало координат принадлежит графику функции.

2. Если x > 0, то y > 0, т.е. график расположен в первой координатной четверти.

3. Большему значению аргумента соответствует большее значение функции ( $0 < x_{1} < x_{2}$ , тогда $\sqrt{x_{1}} < \sqrt{x_{2}}$ ), поэтому график идёт вверх.

Упражнение 1

Используя график функции (рис. 2), определите:

1. Значение функции при х = 2; 3,5; 5,2; 8,5;

2. Значение аргумента, которому соответствует значение функции 0,8; 1,6; 2,3; 2,9.

Пример 1

Сравните числа с помощью свойства функции:

а) $\sqrt{1, 3}$ и $\sqrt{2, 5}$ ; б) $\sqrt{5}$ и $\sqrt{4, 5}$ .

Решение

а) $\sqrt{1, 3} < \sqrt{2, 5}$ , т.к. $1, 3 < 2, 5$ ;

б) $\sqrt{5} > \sqrt{4, 5}$ , т.к. $5 > 4, 5$ .

Ответ: а) $\sqrt{1, 3} < \sqrt{2, 5}$ ; б) $\sqrt{5} > \sqrt{4, 5}$ .

Упражнение 2

Сравните числа с помощью свойств функции:

а) $\sqrt{43}$ и $\sqrt{45}$ ; б) $\sqrt{2, 6}$ и $\sqrt{2, 1}$ ; в) $\sqrt{\frac{1}{10}}$ и $\sqrt{\frac{1}{12}}$ .

Симметрия графиков функций $y = x^{2}$ (при $x \geq 0$ ) и $y = \sqrt{x}$

График функции $y = \sqrt{x}$ , как и график функции $y = x^{2}$ , где $x \geq 0$ , представляет собой ветвь параболы. Эти графики симметричны относительно прямой $y = x$ (рис. 3). Докажем этот факт.

Пусть точка M(a; b) принадлежит графику функции $y = x^{2}$ , где $x \geq 0$ . Тогда верно равенство $a^{2} = b$ . По условию a — неотрицательное число поэтому $a = \sqrt{b}$ . Значит при подстановке координат точки N(b; a) в формулу $y = \sqrt{x}$ получается верное равенство, т.е. точка N(b; a) принадлежит графику функции $y = \sqrt{x}$ .

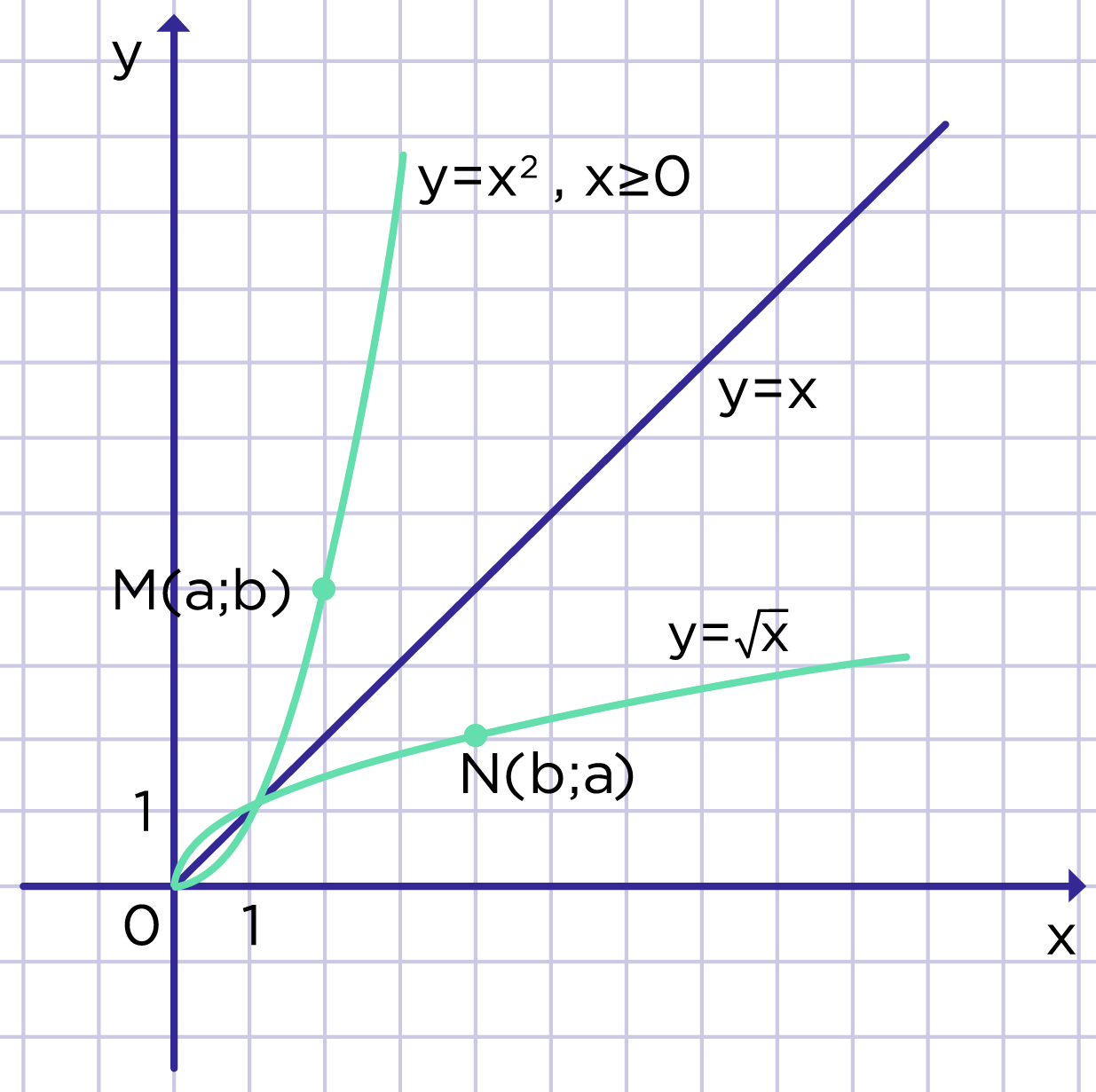Рис. 3. Симметричность графиков функций

Верно и обратное: если точка N(b; a) принадлежит графику функции $y = \sqrt{x}$ , то M(a; b) принадлежит графику функции $y = x^{2}$ , где $x \geq 0$ .

Таким образом, между точкой M(a; b) графика функции $y = x^{2}$ , где $x \geq 0$ , и точкой N(b; a) графика функции $y = \sqrt{x}$ , существует взаимно однозначное соответствие. Т.к. точки M(a; b) и N(b; a) симметричны относительно прямой $y = x$ , то и сами графики симметричны относительно этой прямой.

Графическое решение уравнений вида $\sqrt{x} = k x + b$

Рассмотрим пример решения уравнения вида $\sqrt{x} = k x + b$ графическим способом.

Пример 2

Решите уравнение $\sqrt{x} = 6 - x$ графическим способом.

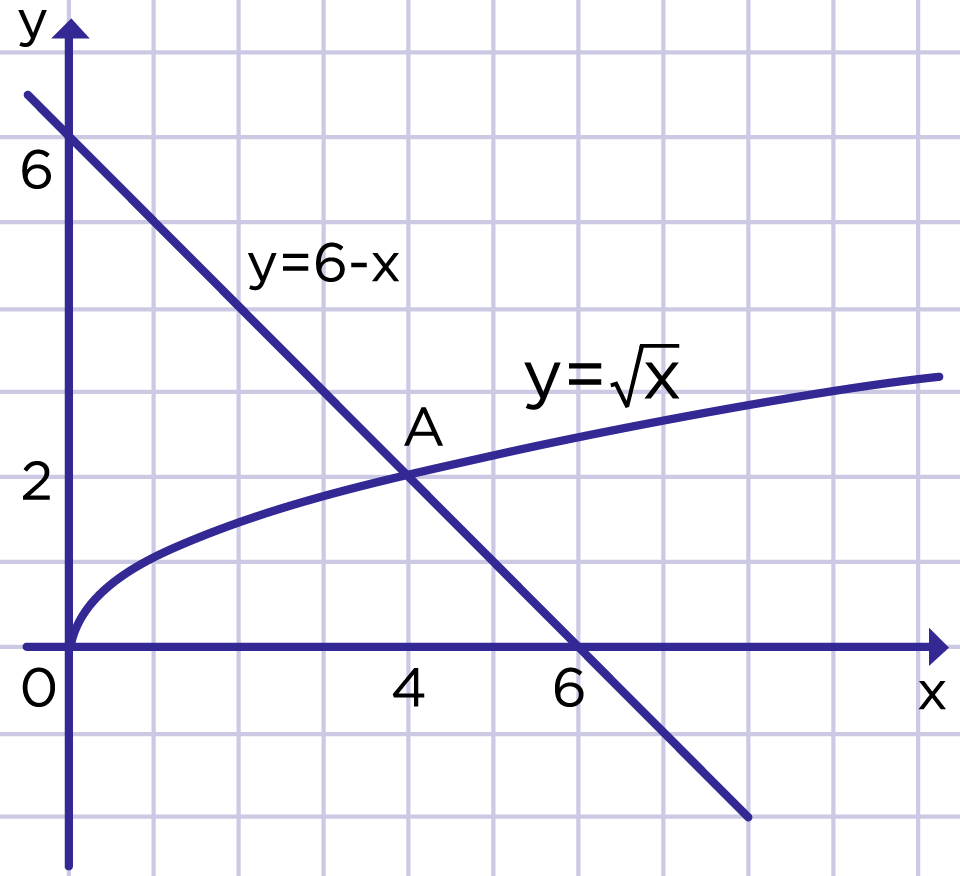Рис. 4. Графическое решение уравнения
√x = 6 – x

Решение

Построим график функции $y = \sqrt{x}$ . График функции $y = 6 - x$ — прямая, которую можно построить по двум точкам (0; 6) и (6; 0). Оба графика изобразим в одной координатной плоскости (рис. 4).

Графики этих функций пересекаются в точке A(4; 2). Если подставить в уравнение вместо x абсциссу этой точки 4, то получим верное равенство:

$\sqrt{4} = 6 - 4$ .

Таким образом, решение уравнения x = 4.

Ответ: 4.

Упражнение 3

Решите уравнение $\sqrt{x} = x - 2$ графическим способом.

Контрольные вопросы

1. Какова область определения функции $y = \sqrt{x}$ ?

2. Как расположен график функции $y = \sqrt{x}$ в координатной плоскости?

3. Пересекает ли прямая $y = a$ , где а — некоторое число, график функции $y = \sqrt{x} ?$

Ответы

Упражнение 1

1. 1,4; 1,9; 2,3; 2,9;

2. 0,6; 2,6; 5,3; 8,4.

Упражнение 2

а) $\sqrt{43}$ < $\sqrt{45}$ ; б) $\sqrt{2, 6}$ > $\sqrt{2, 1}$ ; в) $\sqrt{\frac{1}{10}}$ > $\sqrt{\frac{1}{12}}$ .

Упражнение 3

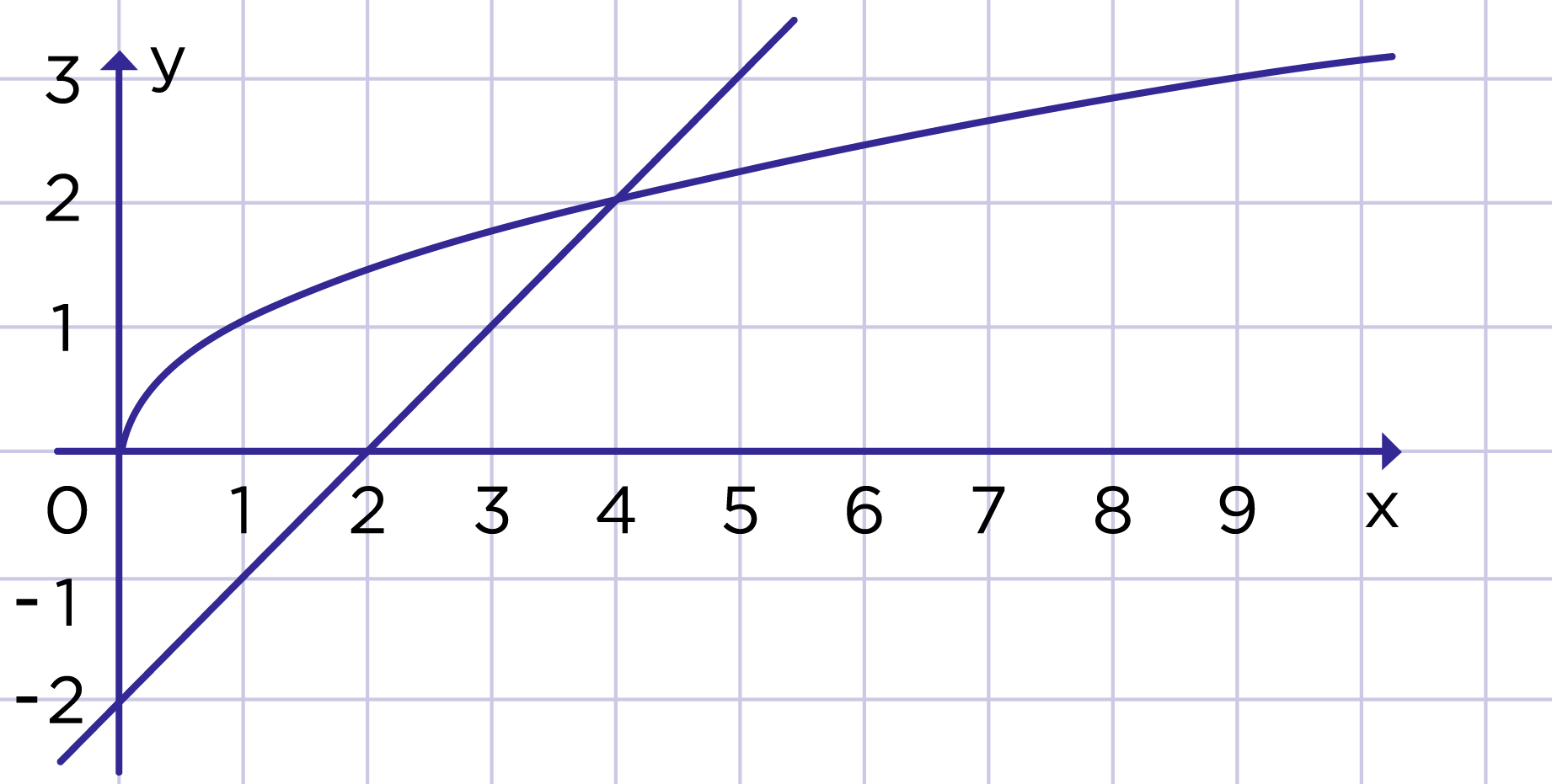Рис. 5. Упражнение 3. Ответ

Конспект урока: Функция корня и её график

Функции

Функция $y = \sqrt{x}$ и ее график

Конспект урока: Функция корня и её график

Функции

Функция y=x и ее график

Функция $y = \sqrt{x}$ и ее график