- Цилиндрическая поверхность;
- Цилиндр;
- Сечения цилиндра;
- Площадь поверхности цилиндра.
- Знать определение цилиндра;
- Знать элементы цилиндра;
- Уметь находить площадь поверхности цилиндра.
- Какую форму имеют трубы?
- Может ли в основании призмы лежать круг? А у пирамиды?
- Каким свойством обладают прямые, перпендикулярные одной плоскости?
Цилиндрическая поверхность
Рассмотрим окружность с центром в точке и радиусом , лежащую в некоторой плоскости . Через каждую точку окружности проведем прямые, перпендикулярные этой окружности. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью. Сами прямые называются образующими цилиндрической поверхности. Прямая, проходящая через точку перпендикулярно плоскости - осью цилиндрической поверхности.
При этом образующие и ось цилиндрической поверхности параллельны, так как перпендикулярны одной плоскости .
Цилиндр
Ограничим цилиндрическую поверхность плоскостью , параллельной плоскости . Образующие цилиндрической поверхности пересекают плоскость в точках, которые образуют окружность равную окружности в плоскости (рис. 1). Тело, ограниченное цилиндрической поверхностью и двумя кругами с границей и называется цилиндром, круги называются основаниями цилиндра.
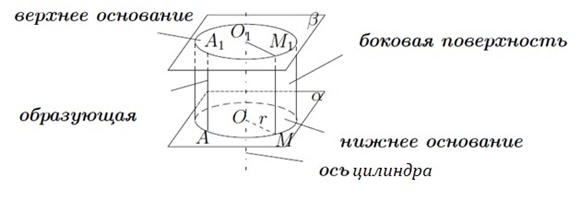 Рис. 1. Цилиндр
Рис. 1. Цилиндр
Образующими цилиндра называют отрезки образующих цилиндрической поверхности, заключенные между основаниями, а боковой поверхностью цилиндра – образованную ими часть цилиндрической поверхности. Ось цилиндрической поверхности является также и осью цилиндра.
Все образующие цилиндра равны друг другу и параллельны. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
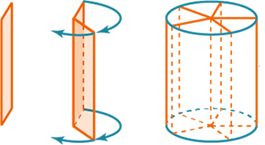 Рис. 2. Цилиндр как фигура вращения
Рис. 2. Цилиндр как фигура вращения
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон (оси вращения) (рис. 2). При этом боковая поверхность цилиндра образуется вращением стороны, параллельной оси вращения, а основания – вращением двух других сторон.
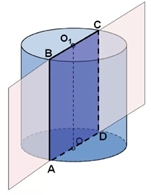 Рис. 3. Осевое сечение
Рис. 3. Осевое сечение
Сечение цилиндра
Построим секущую плоскость, проходящую через ось цилиндра (рис. 3). Полученное сечение – это прямоугольник, две стороны которого – это диаметры оснований, а две другие – образующие цилиндра.
Это сечение называется осевым.
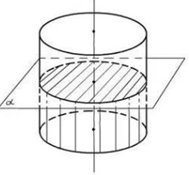 Рис. 4. Сечение параллельное основаниям
Рис. 4. Сечение параллельное основаниям
Теперь построим секущую плоскость, перпендикулярную оси цилиндра (рис. 4). Такое сечение является кругом. Она (плоскость) отсекает от цилиндра тело, также являющееся цилиндром, основания которого равны основаниям исходного цилиндра.
Пример 1
Найдите площадь сечения цилиндра, параллельного его оси, радиус основания которого равен 5, а образующая – 10, если расстояние от оси цилиндра до этой плоскости равно 3.
Решение
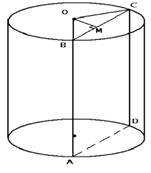 Рис. 5. Цилиндр
Рис. 5. Цилиндр
На рисунке 5 изображено это сечение . Сечение является прямоугольником, одна сторона которого равна образующей цилиндра, а вторая – это хорда основания.
- расстояние от оси цилиндра до плоскости сечения.
Рассмотрим равнобедренный треугольник , где - высота, а значит, - середина . Тогда по теореме Пифагора:
,
.
Тогда площадь сечения:
.
Ответ: 80.
Упражнение 1
Найдите площадь сечения цилиндра параллельного его оси, радиус основания которого равен 8, а образующая – 7, если расстояние от оси цилиндра до этой плоскости равно 4.
Площадь поверхности цилиндра
Чтобы вычислить площадь боковой поверхности цилиндра, необходимо развернуть её на плоскость. Если сделать разрез по образующей цилиндра и развернуть поверхность так, чтобы все образующие лежали в одной плоскости, то получим прямоугольник , одна сторона которого равна образующей (или высоте цилиндра), а другая - длине окружности основания цилиндра (рис. 6).
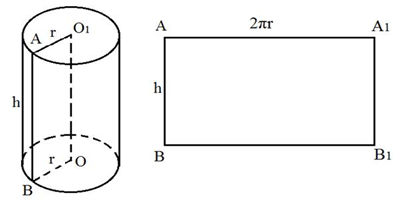 Рис. 6. Боковая поверхность цилиндра
Рис. 6. Боковая поверхность цилиндра
В этом случае, площадь поверхности цилиндра равна площади прямоугольника , т.е.
,
где — радиус основания цилиндра, — высота цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадь полной поверхности цилиндра есть сумма площадей боковой поверхности и двух оснований. Площадь каждого из оснований равна . Тогда для вычисления площади полной поверхности можно воспользоваться формулой:
.
Пример 2
Во сколько раз площадь полной поверхности цилиндра больше боковой поверхности, если радиус основания равен высоте цилиндра?
Решение
При условии, что получаем
,
.
Тогда
.
Ответ: 2.
Упражнение 2
1. Вычислите площадь боковой поверхности цилиндра, если его высота равна 7, а радиус основания равен 3.
2. Во сколько раз площадь полной поверхности цилиндра больше боковой поверхности, если радиус основания в 3 раза меньше высоты цилиндра?
Контрольные вопросы
1. Что такое цилиндр?
2. Какие элементы есть у цилиндра?
3. Что представляет собой боковая поверхность цилиндра?
Упражнение 1
.
Упражнение 2
1. .
2. .
- Цилиндрическая поверхность;
- Цилиндр;
- Сечения цилиндра;
- Площадь поверхности цилиндра.
- Знать определение цилиндра;
- Знать элементы цилиндра;
- Уметь находить площадь поверхности цилиндра.
- Какую форму имеют трубы?
- Может ли в основании призмы лежать круг? А у пирамиды?
- Каким свойством обладают прямые, перпендикулярные одной плоскости?
Цилиндрическая поверхность
Рассмотрим окружность с центром в точке и радиусом , лежащую в некоторой плоскости . Через каждую точку окружности проведем прямые, перпендикулярные этой окружности. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью. Сами прямые называются образующими цилиндрической поверхности. Прямая, проходящая через точку перпендикулярно плоскости - осью цилиндрической поверхности.
При этом образующие и ось цилиндрической поверхности параллельны, так как перпендикулярны одной плоскости .
Цилиндр
Ограничим цилиндрическую поверхность плоскостью , параллельной плоскости . Образующие цилиндрической поверхности пересекают плоскость в точках, которые образуют окружность равную окружности в плоскости (рис. 1). Тело, ограниченное цилиндрической поверхностью и двумя кругами с границей и называется цилиндром, круги называются основаниями цилиндра.
 Рис. 1. Цилиндр
Рис. 1. Цилиндр
Образующими цилиндра называют отрезки образующих цилиндрической поверхности, заключенные между основаниями, а боковой поверхностью цилиндра – образованную ими часть цилиндрической поверхности. Ось цилиндрической поверхности является также и осью цилиндра.
Все образующие цилиндра равны друг другу и параллельны. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
 Рис. 2. Цилиндр как фигура вращения
Рис. 2. Цилиндр как фигура вращения
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон (оси вращения) (рис. 2). При этом боковая поверхность цилиндра образуется вращением стороны, параллельной оси вращения, а основания – вращением двух других сторон.
 Рис. 3. Осевое сечение
Рис. 3. Осевое сечение
Сечение цилиндра
Построим секущую плоскость, проходящую через ось цилиндра (рис. 3). Полученное сечение – это прямоугольник, две стороны которого – это диаметры оснований, а две другие – образующие цилиндра.
Это сечение называется осевым.
 Рис. 4. Сечение параллельное основаниям
Рис. 4. Сечение параллельное основаниям
Теперь построим секущую плоскость, перпендикулярную оси цилиндра (рис. 4). Такое сечение является кругом. Она (плоскость) отсекает от цилиндра тело, также являющееся цилиндром, основания которого равны основаниям исходного цилиндра.
Пример 1
Найдите площадь сечения цилиндра, параллельного его оси, радиус основания которого равен 5, а образующая – 10, если расстояние от оси цилиндра до этой плоскости равно 3.
Решение
 Рис. 5. Цилиндр
Рис. 5. Цилиндр
На рисунке 5 изображено это сечение . Сечение является прямоугольником, одна сторона которого равна образующей цилиндра, а вторая – это хорда основания.
- расстояние от оси цилиндра до плоскости сечения.
Рассмотрим равнобедренный треугольник , где - высота, а значит, - середина . Тогда по теореме Пифагора:
,
.
Тогда площадь сечения:
.
Ответ: 80.
Упражнение 1
Найдите площадь сечения цилиндра параллельного его оси, радиус основания которого равен 8, а образующая – 7, если расстояние от оси цилиндра до этой плоскости равно 4.
Площадь поверхности цилиндра
Чтобы вычислить площадь боковой поверхности цилиндра, необходимо развернуть её на плоскость. Если сделать разрез по образующей цилиндра и развернуть поверхность так, чтобы все образующие лежали в одной плоскости, то получим прямоугольник , одна сторона которого равна образующей (или высоте цилиндра), а другая - длине окружности основания цилиндра (рис. 6).
 Рис. 6. Боковая поверхность цилиндра
Рис. 6. Боковая поверхность цилиндра
В этом случае, площадь поверхности цилиндра равна площади прямоугольника , т.е.
,
где — радиус основания цилиндра, — высота цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадь полной поверхности цилиндра есть сумма площадей боковой поверхности и двух оснований. Площадь каждого из оснований равна . Тогда для вычисления площади полной поверхности можно воспользоваться формулой:
.
Пример 2
Во сколько раз площадь полной поверхности цилиндра больше боковой поверхности, если радиус основания равен высоте цилиндра?
Решение
При условии, что получаем
,
.
Тогда
.
Ответ: 2.
Упражнение 2
1. Вычислите площадь боковой поверхности цилиндра, если его высота равна 7, а радиус основания равен 3.
2. Во сколько раз площадь полной поверхности цилиндра больше боковой поверхности, если радиус основания в 3 раза меньше высоты цилиндра?
Контрольные вопросы
1. Что такое цилиндр?
2. Какие элементы есть у цилиндра?
3. Что представляет собой боковая поверхность цилиндра?
Упражнение 1
.
Упражнение 2
1. .
2. .


