- Сфера и шар
- Взаимное расположение сферы и плоскости
- Касательная плоскость к сфере
- Площадь сферы
- Знать, что такое сфера и шар
- Уметь определять взаимное расположение сферы и плоскости
- Знать теоремы о касательной плоскости к сфере
- Знать формулу площади сферы
- Уметь находить площадь сферы
- Чем круг отличается от окружности?
- Почему конус и цилиндр названы фигурами вращения?
Сфера и шар
Сфера – общенаучное понятие, обозначающее наиболее крупную часть бытия любого уровня: мироздания, физического, химического, биологического, социального и индивидуального миров. Форма шара является весьма распространенной в природе и в окружающей нас обстановке. Самым интересным объектом, имеющим шаровую поверхность, является наша планета Земля.
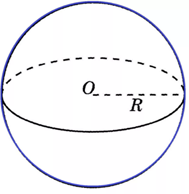 Рис. 1. Сфера
Рис. 1. Сфера
Ни одна наука не обошла своим вниманием понятия сферы и шара. Многие реальные объекты астрономии, биологии, химии и других естественных наук имеют форму этих геометрических фигур. В различные исторические эпохи изучению данных понятий отводилась и отводится значительная роль. Мы рассмотрим эти понятия с геометрической точки зрения.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (рис. 1).
Данная точка называется центром сферы (на рис. 1 – точка ), а данное расстояние – радиусом сферы (обозначают буквой ).
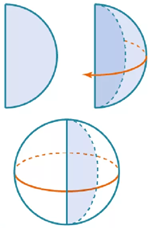 Рис. 2. Сфера как фигура вращения
Рис. 2. Сфера как фигура вращения
Любой отрезок, соединяющий центр сферы с какой-нибудь её точкой, также называется радиусом сферы. Отметим, что у сферы так же, как и у окружности, есть диаметр. Диаметр сферы – это отрезок, соединяющий две точки сферы и проходящий через её центр. Аналогичным образом длина диаметра сферы будет вдвое больше радиуса, т.е. ( – диаметр сферы).
Сфера так же, как цилиндр и конус, является фигурой вращения, так как её можно получить вращением полуокружности вокруг её диаметра (рис. 2).
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Взаимное расположение сферы и плоскости
Рассмотрим взаимное расположение сферы и плоскости.
Проведем аналогию с парой – окружность и прямая.
Вспомним, что окружность и прямая могут не пересекаться (если расстояние от центра окружности до прямой больше радиуса), прямая может быть касательной к окружности (расстояние равно радиусу) и прямая может пересекать окружность (расстояние меньше радиуса).
Тогда можно сделать вывод, что сфера и плоскость имеют аналогичное взаимное расположение. Но сначала сделаем ещё один вывод.
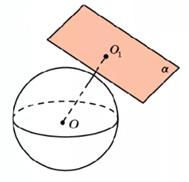 Рис. 3. Сфера и плоскость не пересекаются
Рис. 3. Сфера и плоскость не пересекаются
Если точка лежит на сфере, то расстояние от этой точки до центра сферы равно радиусу (по определению радиуса сферы). Тогда если точка лежит вне сферы (снаружи), то расстояние между этой точкой и сферой больше радиуса, и, наоборот, если точка лежит внутри сферы, то радиус сферы больше расстояния от этой точки до центра сферы.
Начнем с первого случая. Пусть сфера и плоскость не пересекаются, т.е. не имеют общих точек (рис. 3). Значит, расстояние от любой точки плоскости до центра сферы больше радиуса этой сферы. Пусть отрезок 𝑂𝑂1 − расстояние от центра сферы до плоскости. Тогда длина этого отрезка больше радиуса
сферы, т.е. .
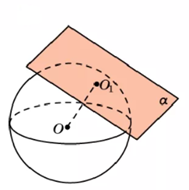 Рис. 4. Касательная плоскость к сфере
Рис. 4. Касательная плоскость к сфере
Рассмотрим теперь случай касания (рис. 4). Плоскость будем называть касательной к сфере, если она имеет только одну общую точку. Пусть − точка касания плоскости и сферы, значит, точка принадлежит как плоскости, так и прямой. Значит, отрезок, соединяющий центр окружности с этой точкой является радиусом, т.е. . Причём, − расстояние от центра сферы до плоскости, так как расстояние от центра сферы до любой другой точки плоскости, не принадлежащей сфере, будет больше радиуса, т.е. − наименьшее расстояние от центра до точки плоскости.
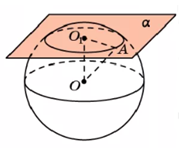 Рис. 5. Плоскость пересекает сферу
Рис. 5. Плоскость пересекает сферу
Пусть теперь плоскость пересекает сферу (рис. 5). Тогда часть плоскости лежит внутри сферы. Пусть отрезок − расстояние от центра сферы до плоскости, а отрезок − отрезок, соединяющий центр сферы с точкой пересечения сферы и плоскости ( является радиусом сферы). Тогда − наклонная к плоскости, т.е. или .
Таким образом, мы получили условия взаимного расположения сферы и плоскости. Пусть − расстояние от центра сферы до плоскости, − радиус сферы. Тогда можем подвести следующий итог.
Сфера и плоскость не пересекаются, если расстояние от центра сферы до плоскости больше радиуса сферы, т.е. .
Плоскость является касательной к сфере, если расстояние от центра сферы до плоскости равно радиусу сферы, т.е. .
Сфера и плоскость пересекаются, если расстояние от центра сферы до плоскости меньше радиуса сферы, т.е. .
Касательная плоскость к сфере
Рассматривая случай касания сферы и плоскости, мы ввели несколько определений.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Также мы пришли к выводу, что длина отрезка, соединяющего точку касания с центром сферы, является расстоянием от центра сферы до этой плоскости. Этот вывод выражен в следующей теореме.
Теорема
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Доказать это достаточно просто.
Допустим, что это не так. Тогда радиус является наклонной к плоскости, и, тогда расстояние от центра сферы до плоскости меньше радиуса, что означает пересечение сферы и плоскости. А это противоречит тому, что плоскость касательная. Получили противоречие. Значит, радиус перпендикулярен к касательной плоскости.
Существует и обратная теорема.
Теорема
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то это плоскость является касательной к сфере.
Доказательство аналогичное.
Радиус, перпендикулярный плоскости, является расстоянием от центра сферы до этой плоскости, т.е. . Из чего следует, что плоскость является касательной к сфере.
Площадь сферы
Чтобы получить формулы для нахождения площадей поверхности цилиндра и конуса, мы использовали развертки этих фигур. Для сферы такой развертки не существует. Значит, получить формулу площади сферы из геометрических соображений не получится.
Для этого существуют методы математического анализа, о которых мы подробно поговорим в следующих темах.
А сейчас определим эту формулу.
Формула для вычисления площади сферы радиуса имеет вид:
.
Пример 1
Найти площадь сферы радиуса .
Решение
Подставим в формулу значение радиуса, получим:
.
Ответ: .
Упражнение 1
1. Найти площадь сферы радиуса если:
а) ;
б) ;
в) .
2. Найти радиус сферы, если:
а) ;
б) ,
в) .
Контрольные вопросы
1. Чем сфера отличается от шара?
2. Как могут быть взаимно расположены сфера и плоскость?
3. Каким свойством обладает радиус, проведенный в точку касания сферы и плоскости?
4. Назовите формулу площади сферы.
Упражнение 1
1. а) ;
б) ;
в) .
2. а) 7;
б) 0,2;
в) 5,5.
- Сфера и шар
- Взаимное расположение сферы и плоскости
- Касательная плоскость к сфере
- Площадь сферы
- Знать, что такое сфера и шар
- Уметь определять взаимное расположение сферы и плоскости
- Знать теоремы о касательной плоскости к сфере
- Знать формулу площади сферы
- Уметь находить площадь сферы
- Чем круг отличается от окружности?
- Почему конус и цилиндр названы фигурами вращения?
Сфера и шар
Сфера – общенаучное понятие, обозначающее наиболее крупную часть бытия любого уровня: мироздания, физического, химического, биологического, социального и индивидуального миров. Форма шара является весьма распространенной в природе и в окружающей нас обстановке. Самым интересным объектом, имеющим шаровую поверхность, является наша планета Земля.
 Рис. 1. Сфера
Рис. 1. Сфера
Ни одна наука не обошла своим вниманием понятия сферы и шара. Многие реальные объекты астрономии, биологии, химии и других естественных наук имеют форму этих геометрических фигур. В различные исторические эпохи изучению данных понятий отводилась и отводится значительная роль. Мы рассмотрим эти понятия с геометрической точки зрения.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (рис. 1).
Данная точка называется центром сферы (на рис. 1 – точка ), а данное расстояние – радиусом сферы (обозначают буквой ).
 Рис. 2. Сфера как фигура вращения
Рис. 2. Сфера как фигура вращения
Любой отрезок, соединяющий центр сферы с какой-нибудь её точкой, также называется радиусом сферы. Отметим, что у сферы так же, как и у окружности, есть диаметр. Диаметр сферы – это отрезок, соединяющий две точки сферы и проходящий через её центр. Аналогичным образом длина диаметра сферы будет вдвое больше радиуса, т.е. ( – диаметр сферы).
Сфера так же, как цилиндр и конус, является фигурой вращения, так как её можно получить вращением полуокружности вокруг её диаметра (рис. 2).
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Взаимное расположение сферы и плоскости
Рассмотрим взаимное расположение сферы и плоскости.
Проведем аналогию с парой – окружность и прямая.
Вспомним, что окружность и прямая могут не пересекаться (если расстояние от центра окружности до прямой больше радиуса), прямая может быть касательной к окружности (расстояние равно радиусу) и прямая может пересекать окружность (расстояние меньше радиуса).
Тогда можно сделать вывод, что сфера и плоскость имеют аналогичное взаимное расположение. Но сначала сделаем ещё один вывод.
 Рис. 3. Сфера и плоскость не пересекаются
Рис. 3. Сфера и плоскость не пересекаются
Если точка лежит на сфере, то расстояние от этой точки до центра сферы равно радиусу (по определению радиуса сферы). Тогда если точка лежит вне сферы (снаружи), то расстояние между этой точкой и сферой больше радиуса, и, наоборот, если точка лежит внутри сферы, то радиус сферы больше расстояния от этой точки до центра сферы.
Начнем с первого случая. Пусть сфера и плоскость не пересекаются, т.е. не имеют общих точек (рис. 3). Значит, расстояние от любой точки плоскости до центра сферы больше радиуса этой сферы. Пусть отрезок 𝑂𝑂1 − расстояние от центра сферы до плоскости. Тогда длина этого отрезка больше радиуса
сферы, т.е. .
 Рис. 4. Касательная плоскость к сфере
Рис. 4. Касательная плоскость к сфере
Рассмотрим теперь случай касания (рис. 4). Плоскость будем называть касательной к сфере, если она имеет только одну общую точку. Пусть − точка касания плоскости и сферы, значит, точка принадлежит как плоскости, так и прямой. Значит, отрезок, соединяющий центр окружности с этой точкой является радиусом, т.е. . Причём, − расстояние от центра сферы до плоскости, так как расстояние от центра сферы до любой другой точки плоскости, не принадлежащей сфере, будет больше радиуса, т.е. − наименьшее расстояние от центра до точки плоскости.
 Рис. 5. Плоскость пересекает сферу
Рис. 5. Плоскость пересекает сферу
Пусть теперь плоскость пересекает сферу (рис. 5). Тогда часть плоскости лежит внутри сферы. Пусть отрезок − расстояние от центра сферы до плоскости, а отрезок − отрезок, соединяющий центр сферы с точкой пересечения сферы и плоскости ( является радиусом сферы). Тогда − наклонная к плоскости, т.е. или .
Таким образом, мы получили условия взаимного расположения сферы и плоскости. Пусть − расстояние от центра сферы до плоскости, − радиус сферы. Тогда можем подвести следующий итог.
Сфера и плоскость не пересекаются, если расстояние от центра сферы до плоскости больше радиуса сферы, т.е. .
Плоскость является касательной к сфере, если расстояние от центра сферы до плоскости равно радиусу сферы, т.е. .
Сфера и плоскость пересекаются, если расстояние от центра сферы до плоскости меньше радиуса сферы, т.е. .
Касательная плоскость к сфере
Рассматривая случай касания сферы и плоскости, мы ввели несколько определений.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Также мы пришли к выводу, что длина отрезка, соединяющего точку касания с центром сферы, является расстоянием от центра сферы до этой плоскости. Этот вывод выражен в следующей теореме.
Теорема
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Доказать это достаточно просто.
Допустим, что это не так. Тогда радиус является наклонной к плоскости, и, тогда расстояние от центра сферы до плоскости меньше радиуса, что означает пересечение сферы и плоскости. А это противоречит тому, что плоскость касательная. Получили противоречие. Значит, радиус перпендикулярен к касательной плоскости.
Существует и обратная теорема.
Теорема
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то это плоскость является касательной к сфере.
Доказательство аналогичное.
Радиус, перпендикулярный плоскости, является расстоянием от центра сферы до этой плоскости, т.е. . Из чего следует, что плоскость является касательной к сфере.
Площадь сферы
Чтобы получить формулы для нахождения площадей поверхности цилиндра и конуса, мы использовали развертки этих фигур. Для сферы такой развертки не существует. Значит, получить формулу площади сферы из геометрических соображений не получится.
Для этого существуют методы математического анализа, о которых мы подробно поговорим в следующих темах.
А сейчас определим эту формулу.
Формула для вычисления площади сферы радиуса имеет вид:
.
Пример 1
Найти площадь сферы радиуса .
Решение
Подставим в формулу значение радиуса, получим:
.
Ответ: .
Упражнение 1
1. Найти площадь сферы радиуса если:
а) ;
б) ;
в) .
2. Найти радиус сферы, если:
а) ;
б) ,
в) .
Контрольные вопросы
1. Чем сфера отличается от шара?
2. Как могут быть взаимно расположены сфера и плоскость?
3. Каким свойством обладает радиус, проведенный в точку касания сферы и плоскости?
4. Назовите формулу площади сферы.
Упражнение 1
1. а) ;
б) ;
в) .
2. а) 7;
б) 0,2;
в) 5,5.
