- Конус;
- Вычисление площади боковой поверхности и объема конуса.
- Знать, что такое конус, его составные элементы;
- Знать формулу нахождения объема конуса;
- Уметь вычислять объем конуса;
- Знать формулу площади боковой поверхности конуса;
- Уметь вычислять площадь боковой поверхности конуса.
- Как образуются тела и поверхности вращения?
- Что такое цилиндр?
- Какие составные элементы цилиндра вы знаете?
- Что такое образующая цилиндра?
- Что такое цилиндрическая поверхность?
- Чему равна площадь боковой поверхности цилиндра?
- Как найти объем цилиндра?
Конус
Возьмем прямоугольный треугольник и будем вращать его вокруг катета (рис. 1). В результате получим тело вращения, называемое конусом.
Конус – фигура, полученная вращением прямоугольного треугольника вокруг одного из его катетов.
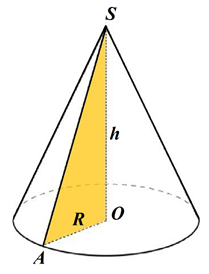 Рис. 1. Конус
Рис. 1. Конус
Поверхность, описанная прямой при ее вращении около оси , называется конической поверхностью конуса или боковой поверхностью конуса.
Прямая называется образующей (обозначается ) конической поверхности или образующей конуса.
Катет вращающегося треугольника описывает круг, называемый основанием конуса.
Длина неподвижного катета называется высотой конуса.
Таким образом, можно сказать, что конус – это тело, ограниченное кругом и конической поверхностью.
Ось вращения называется осью конуса. Неподвижная вершина острого угла называется вершиной конуса.
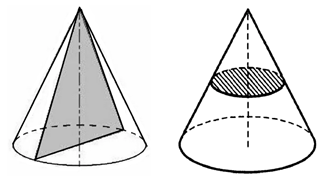 Рис. 2. Сечение конуса
Рис. 2. Сечение конуса
Осевое сечение конуса, проходящее через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 2). Всякое сечение конуса, перпендикулярное к оси, будет круг. Радиус этого круга возрастает по мере удаления от вершины пропорционально расстоянию сечения от вершины.
Вычисление площади боковой поверхности и объема конуса
Объем конуса равен одной трети произведения основания на высоту
Так как основанием конуса является круг, а его площадь равна , то объем конуса также можно вычислить по формуле:
Пример 1
Найдите объем конуса, если диаметр его основания равен 8 см, а высота равна 6 см ().
Решение
Сначала найдем радиус основания, как половину диаметра:
см.
Найдем объем конуса по формуле:
см3.
Ответ: 100,48 см3.
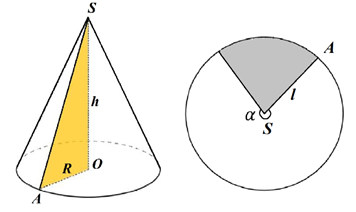 Рис. 3. Развёртка боковой поверхности конуса
Рис. 3. Развёртка боковой поверхности конуса
Развёрткой боковой поверхности конуса будет круговой сектор (рис. 3).
Радиус этого сектора равен образующей конуса , а длина дуги сектора равна длине окружности основания конуса, то есть равна .
Площадь боковой поверхности конуса равна площади ее развертки, т.е.
,
где - градусная мера дуги сектора, - образующая.
Длина дуги окружности с градусной мерой и радиусом равным будет равна . Но, с другой стороны, длина дуги равна , т.е.
,
поэтому
.
Площадь боковой поверхности конуса выражается формулой:
,
где - образующая конуса, - радиус основания.
Площадь полной поверхности конуса состоит из площади основания и площади боковой поверхности. Таким образом:
.
Пример 2
Найдите площадь боковой поверхности конуса, у которого диаметр основания равен 13 см, а образующая равна 20 см. Чему будет равна площадь всей поверхности конуса ()?
Решение
Сначала найдем радиус основания, как половину длины диаметра:
см.
Найдем площадь боковой поверхности конуса по формуле :
см2.
Найдем площадь основания конуса :
см2.
Найдем площадь поверхности конуса как сумму площади боковой поверхности и площади основания:
см2.
Ответ: 408,2 см2, 540,865 см2.
Пример 3
Площадь полной поверхности конуса равна дм2. Развертка боковой поверхности конуса представляет собой круговой сектор с дугой 60°. Найдите объем конуса.
Решение
Воспользуемся формулой площади боковой поверхности конуса :
С другой стороны, по формуле получим, что:
.
Отсюда .
Из формулы выразим, чему равна площадь основания:
Основанием является круг, площадь которого равна . Тогда:
.
Подставим и получим: .
Чтобы вычислить объем, нам нужно знать высоту конуса. Ее можно найти по теореме Пифагора как неизвестный катет:
дм.
Вычислим объем конуса по формуле :
дм3.
Ответ: дм3.
Упражнение 1
1. Найдите объем конуса, если диаметр его основания равен 14 см, а высота равна 9 см ().
2. Найдите площадь боковой поверхности конуса, у которого диаметр основания равен 14 см, а образующая равна 18 см. Чему будет равна площадь всей поверхности конуса ()?
3. Осевым сечением конуса является правильный треугольник со стороной 6 см. Найдите объем конуса.
Контрольные вопросы
1. Какая фигура называется конусом?
2. Что такое образующая конуса?
3. Чему равен объем конуса?
4. Чему равна площадь боковой поверхности конуса?
5. Чему равна общая площадь поверхности конуса?
Упражнение 1
1. 461,58 см3. 2. 395,64 см2, 549,5 см2. 3
- Конус;
- Вычисление площади боковой поверхности и объема конуса.
- Знать, что такое конус, его составные элементы;
- Знать формулу нахождения объема конуса;
- Уметь вычислять объем конуса;
- Знать формулу площади боковой поверхности конуса;
- Уметь вычислять площадь боковой поверхности конуса.
- Как образуются тела и поверхности вращения?
- Что такое цилиндр?
- Какие составные элементы цилиндра вы знаете?
- Что такое образующая цилиндра?
- Что такое цилиндрическая поверхность?
- Чему равна площадь боковой поверхности цилиндра?
- Как найти объем цилиндра?
Конус
Возьмем прямоугольный треугольник и будем вращать его вокруг катета (рис. 1). В результате получим тело вращения, называемое конусом.
Конус – фигура, полученная вращением прямоугольного треугольника вокруг одного из его катетов.
 Рис. 1. Конус
Рис. 1. Конус
Поверхность, описанная прямой при ее вращении около оси , называется конической поверхностью конуса или боковой поверхностью конуса.
Прямая называется образующей (обозначается ) конической поверхности или образующей конуса.
Катет вращающегося треугольника описывает круг, называемый основанием конуса.
Длина неподвижного катета называется высотой конуса.
Таким образом, можно сказать, что конус – это тело, ограниченное кругом и конической поверхностью.
Ось вращения называется осью конуса. Неподвижная вершина острого угла называется вершиной конуса.
 Рис. 2. Сечение конуса
Рис. 2. Сечение конуса
Осевое сечение конуса, проходящее через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 2). Всякое сечение конуса, перпендикулярное к оси, будет круг. Радиус этого круга возрастает по мере удаления от вершины пропорционально расстоянию сечения от вершины.
Вычисление площади боковой поверхности и объема конуса
Объем конуса равен одной трети произведения основания на высоту
Так как основанием конуса является круг, а его площадь равна , то объем конуса также можно вычислить по формуле:
Пример 1
Найдите объем конуса, если диаметр его основания равен 8 см, а высота равна 6 см ().
Решение
Сначала найдем радиус основания, как половину диаметра:
см.
Найдем объем конуса по формуле:
см3.
Ответ: 100,48 см3.
 Рис. 3. Развёртка боковой поверхности конуса
Рис. 3. Развёртка боковой поверхности конуса
Развёрткой боковой поверхности конуса будет круговой сектор (рис. 3).
Радиус этого сектора равен образующей конуса , а длина дуги сектора равна длине окружности основания конуса, то есть равна .
Площадь боковой поверхности конуса равна площади ее развертки, т.е.
,
где - градусная мера дуги сектора, - образующая.
Длина дуги окружности с градусной мерой и радиусом равным будет равна . Но, с другой стороны, длина дуги равна , т.е.
,
поэтому
.
Площадь боковой поверхности конуса выражается формулой:
,
где - образующая конуса, - радиус основания.
Площадь полной поверхности конуса состоит из площади основания и площади боковой поверхности. Таким образом:
.
Пример 2
Найдите площадь боковой поверхности конуса, у которого диаметр основания равен 13 см, а образующая равна 20 см. Чему будет равна площадь всей поверхности конуса ()?
Решение
Сначала найдем радиус основания, как половину длины диаметра:
см.
Найдем площадь боковой поверхности конуса по формуле :
см2.
Найдем площадь основания конуса :
см2.
Найдем площадь поверхности конуса как сумму площади боковой поверхности и площади основания:
см2.
Ответ: 408,2 см2, 540,865 см2.
Пример 3
Площадь полной поверхности конуса равна дм2. Развертка боковой поверхности конуса представляет собой круговой сектор с дугой 60°. Найдите объем конуса.
Решение
Воспользуемся формулой площади боковой поверхности конуса :
С другой стороны, по формуле получим, что:
.
Отсюда .
Из формулы выразим, чему равна площадь основания:
Основанием является круг, площадь которого равна . Тогда:
.
Подставим и получим: .
Чтобы вычислить объем, нам нужно знать высоту конуса. Ее можно найти по теореме Пифагора как неизвестный катет:
дм.
Вычислим объем конуса по формуле :
дм3.
Ответ: дм3.
Упражнение 1
1. Найдите объем конуса, если диаметр его основания равен 14 см, а высота равна 9 см ().
2. Найдите площадь боковой поверхности конуса, у которого диаметр основания равен 14 см, а образующая равна 18 см. Чему будет равна площадь всей поверхности конуса ()?
3. Осевым сечением конуса является правильный треугольник со стороной 6 см. Найдите объем конуса.
Контрольные вопросы
1. Какая фигура называется конусом?
2. Что такое образующая конуса?
3. Чему равен объем конуса?
4. Чему равна площадь боковой поверхности конуса?
5. Чему равна общая площадь поверхности конуса?
Упражнение 1
1. 461,58 см3. 2. 395,64 см2, 549,5 см2. 3



