- Сфера и шар.
- Знать, что такое сфера, ее центр, радиус и диаметр;
- Знать определение шара;
- Знать формулу площади сферы;
- Уметь вычислять площадь сферы;
- Знать формулу объема шара;
- Уметь вычислять объем шара.
- Какая фигура называется конусом?
- Что такое цилиндр?
- Что такое коническая поверхность?
- Чему равна площадь боковой поверхности конуса?
- Как найти объем конуса?
Сфера и шар
Сфера – поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки (рис. 1).
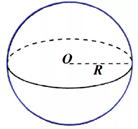 Рис. 1. Сфера
Рис. 1. Сфера
На рисунке 1 данная точка О называется центром сферы, а заданное расстояние на рисунке обозначено и называется радиусом сферы. Также и любой отрезок, который соединяет любую точку сферы с ее центром, будет являться радиусом.
Диаметром сферы называется отрезок, который соединяет две точки сферы и проходит через ее центр. Понятно, что диаметр сферы в два раза больше ее радиуса, т.е. равен .
Шар – тело, ограниченное сферой.
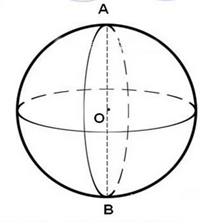 Рис. 2. Шар
Рис. 2. Шар
Центр, радиус и диаметр сферы также будут центром, радиусом и диаметром шара. Очевидно, что шар радиуса с центром содержит все точки пространства, расположенные от точки на расстоянии, не превышающем (включая и саму точку ), и не содержит других точек.
Шар получается при вращении полукруга или круга вокруг его диаметра как оси (рис. 2).
Заметим, что в отличие от всяких других круглых тел шар имеет не одну, а бесчисленное множество осей. Любой диаметр может служить осью шара. Концы любого диаметра называются диаметрально противоположными точками шара.
Любое сечение шара плоскостью будет являться кругом. Если секущая плоскость проходит через центр, в сечении получается круг, радиус которого равен радиусу шара. Такой круг называется большим кругом. Круг, плоскость которого не проходит через центр шара, называется малым кругом. Например, меридианы земного шара – это большие круги, а параллели (кроме экватора) – это малые круги. Экватор будет большим кругом.
Поверхность шара, даже если ее разрезать на части, нельзя развернуть на плоскости и представить в виде плоской фигуры. Поэтому для сферы не пригоден способ вычисления площади с помощью развёртки.
Площадь сферической поверхности шара ровно в четыре раза больше площади его большого круга. Т.е.
.
Объем шара радиуса находится по формуле:
.
Доказательство этих формул будет рассмотрено в курсе стереометрии 11 класса.
Пример 1
Найдите площадь сферы, диаметр которой равен 12 см ().
Решение
Сначала найдем радиус, как половину диаметра:
см.
Найдем площадь сферы по формуле:
см2.
Ответ: 452,16 см2.
Пример 2
Найдите объем шара, диаметр которого равен 18 см ().
Решение
Сначала найдем радиус, как половину длины диаметра:
см.
Найдем объем шара по формуле :
см3.
Ответ: 3052,08 см3.
Пример 3
Отношение объемов двух шаров равно 27. Найдите, как относятся площади их поверхностей.
Решение
Составим отношение объемов двух шаров:
.
Отсюда , тогда .
.
Ответ: 9.
Упражнение 1
1. Найдите площадь сферы, диаметр которой равен 8 см ().
2. Найдите объем шара, диаметр которого равен 15 см ().
3. Отношение объемов двух шаров равно 8. Найдите, как относятся площади их поверхностей.
Контрольные вопросы
1. Что называется сферой?
2. Какое геометрическое тело называется шаром?
3. Что такое центр, радиус и диаметр сферы?
4. По какой формуле вычисляется площадь сферы?
5. По какой формуле вычисляется объем шара?
Упражнение 1
1. 200,96 см2. 2. 1766,25 см3. 3. 4
- Сфера и шар.
- Знать, что такое сфера, ее центр, радиус и диаметр;
- Знать определение шара;
- Знать формулу площади сферы;
- Уметь вычислять площадь сферы;
- Знать формулу объема шара;
- Уметь вычислять объем шара.
- Какая фигура называется конусом?
- Что такое цилиндр?
- Что такое коническая поверхность?
- Чему равна площадь боковой поверхности конуса?
- Как найти объем конуса?
Сфера и шар
Сфера – поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки (рис. 1).
 Рис. 1. Сфера
Рис. 1. Сфера
На рисунке 1 данная точка О называется центром сферы, а заданное расстояние на рисунке обозначено и называется радиусом сферы. Также и любой отрезок, который соединяет любую точку сферы с ее центром, будет являться радиусом.
Диаметром сферы называется отрезок, который соединяет две точки сферы и проходит через ее центр. Понятно, что диаметр сферы в два раза больше ее радиуса, т.е. равен .
Шар – тело, ограниченное сферой.
 Рис. 2. Шар
Рис. 2. Шар
Центр, радиус и диаметр сферы также будут центром, радиусом и диаметром шара. Очевидно, что шар радиуса с центром содержит все точки пространства, расположенные от точки на расстоянии, не превышающем (включая и саму точку ), и не содержит других точек.
Шар получается при вращении полукруга или круга вокруг его диаметра как оси (рис. 2).
Заметим, что в отличие от всяких других круглых тел шар имеет не одну, а бесчисленное множество осей. Любой диаметр может служить осью шара. Концы любого диаметра называются диаметрально противоположными точками шара.
Любое сечение шара плоскостью будет являться кругом. Если секущая плоскость проходит через центр, в сечении получается круг, радиус которого равен радиусу шара. Такой круг называется большим кругом. Круг, плоскость которого не проходит через центр шара, называется малым кругом. Например, меридианы земного шара – это большие круги, а параллели (кроме экватора) – это малые круги. Экватор будет большим кругом.
Поверхность шара, даже если ее разрезать на части, нельзя развернуть на плоскости и представить в виде плоской фигуры. Поэтому для сферы не пригоден способ вычисления площади с помощью развёртки.
Площадь сферической поверхности шара ровно в четыре раза больше площади его большого круга. Т.е.
.
Объем шара радиуса находится по формуле:
.
Доказательство этих формул будет рассмотрено в курсе стереометрии 11 класса.
Пример 1
Найдите площадь сферы, диаметр которой равен 12 см ().
Решение
Сначала найдем радиус, как половину диаметра:
см.
Найдем площадь сферы по формуле:
см2.
Ответ: 452,16 см2.
Пример 2
Найдите объем шара, диаметр которого равен 18 см ().
Решение
Сначала найдем радиус, как половину длины диаметра:
см.
Найдем объем шара по формуле :
см3.
Ответ: 3052,08 см3.
Пример 3
Отношение объемов двух шаров равно 27. Найдите, как относятся площади их поверхностей.
Решение
Составим отношение объемов двух шаров:
.
Отсюда , тогда .
.
Ответ: 9.
Упражнение 1
1. Найдите площадь сферы, диаметр которой равен 8 см ().
2. Найдите объем шара, диаметр которого равен 15 см ().
3. Отношение объемов двух шаров равно 8. Найдите, как относятся площади их поверхностей.
Контрольные вопросы
1. Что называется сферой?
2. Какое геометрическое тело называется шаром?
3. Что такое центр, радиус и диаметр сферы?
4. По какой формуле вычисляется площадь сферы?
5. По какой формуле вычисляется объем шара?
Упражнение 1
1. 200,96 см2. 2. 1766,25 см3. 3. 4



