- Тела и поверхности вращения;
- Вычисление площади боковой поверхности и объема цилиндра.
- Знать, что такое тела и поверхности вращения;
- Знать, что такое цилиндр и его составные элементы;
- Знать, что такое осевое сечение цилиндра;
- Знать формулу объема цилиндра;
- Знать, что такое развертка боковой поверхности цилиндра и чему равна ее площадь;
- Уметь находить полную площадь боковой поверхности прямого цилиндра, объем цилиндра.
- Какой многогранник называется пирамидой?
- Что такое призма?
- Какие составные элементы пирамиды вы знаете?
- Какая пирамида называется правильной?
- Что такое апофема правильной пирамиды?
- Чему равна площадь боковой поверхности правильной пирамиды?
- Как найти площадь полной поверхности пирамиды?
- Чему равна площадь круга? Длина окружности?
Тела и поверхности вращения. Цилиндр
Тело, образуемое вращением какой-нибудь плоской фигуры около неподвижной прямой линии, называется телом вращения. Неподвижная прямая называется осью вращения.
Вырежем из картона прямоугольник и насадим его на ось и будем очень быстро вращать вокруг этой оси. Наш глаз примерно в течении секунды удерживает зрительное впечатление. Поэтому, если прямоугольник будет делать 15-20 оборотов в секунду, мы перестанем различать отдельные его положения, а увидим сплошное круглое тело.
Цилиндр – фигура, полученная вращением прямоугольника вокруг одной из его сторон.
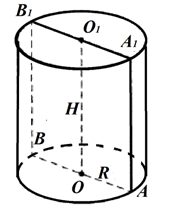 Рис. 1. Цилиндр
Рис. 1. Цилиндр
На рисунке 1 цилиндр, полученный вращением прямоугольника вокруг одной из его сторон или прямоугольника вокруг прямой , которая проходит через серединные точки противолежащих сторон.
Прямая называется осью цилиндра, отрезки и – образующие цилиндра. В качестве высоты цилиндра можно выбрать любой из отрезков . Два круга, лежащих в параллельных плоскостях, которые образовались при вращении, называют основаниями цилиндра. Радиус цилиндра – это радиус его основания .
При вращении стороны , образуется поверхность, состоящая из множества отрезков (образующих цилиндра), параллельных оси цилиндра. Ее называют цилиндрической или боковой поверхностью.
Таким образом, цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра является прямоугольник (рис. 1).
Тела, имеющие форму цилиндра, встречаются довольно часто. Оси колес, стержни, валы, колонны, столбы, обтесанные бревна и многие другие предметы имеют форму цилиндра. Например, трубы, банки, стаканы, ведра имеют форму цилиндра, пустого внутри.
Объем цилиндра равен произведению площади основания на высоту
,
где – объем цилиндра, – площадь основания, - высота цилиндра.
Так как основанием цилиндра является круг, а его площадь равна , то объем цилиндра также можно вычислить по формуле:
.
Пример 1
Найдите объем цилиндра, если диаметр его основания равен 12 см, а высота равна 5 см .
Решение
Сначала найдем радиус основания, как половину диаметра:
см.
Найдем объем цилиндра по формуле :
см3.
Ответ: 565,2 см3.
На рисунке 2 изображен цилиндр. Представьте себе,что его боковую часть разрезали по образующей и развернули таким образом, что получился прямоугольник. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Длина данного прямоугольника равна длине окружности основания, а ширина равна высоте цилиндра. Таким образом, легко получить формулу для вычисления площади боковой поверхности цилиндра.
 Рис. 2. Развёртка боковой поверхности цилиндра
Рис. 2. Развёртка боковой поверхности цилиндра
Площадь боковой поверхности цилиндра равна площади ее развертки и находится по формуле:
.
Площадь полной поверхности прямого цилиндра состоит из двух равных площадей оснований и площади боковой поверхности. Таким образом:
.
Пример 2
Точки и – центры оснований цилиндра, – радиус основания, – образующая цилиндра. Найдите площадь боковой поверхности и объем цилиндра, если см, см .
Решение
Радиус основания цилиндра см, будет являться высотой, т.е. см.
Найдем площадь боковой поверхности по формуле:
см2
2. Найдем объем по формуле:
см3
Ответ: 113,04 см2, 169,56 см3.
Упражнение 1
1. Найдите объем цилиндра, если диаметр его основания равен 20 см, а высота равна 12 см .
2. Точки и – центры оснований цилиндра, – радиус основания. Найдите площадь боковой поверхности и объем цилиндра, если см, см .
Контрольные вопросы
1. Объясните, какое тело называется цилиндром?
2. Объясните, что такое цилиндрическая поверхность?
3. По какой формуле можно найти объем цилиндра?
4. Как вычислить площадь боковой поверхности цилиндра?
Упражнение 1
1. 3768 см3;
2. 226,08 см2, 452,16 см3.
- Тела и поверхности вращения;
- Вычисление площади боковой поверхности и объема цилиндра.
- Знать, что такое тела и поверхности вращения;
- Знать, что такое цилиндр и его составные элементы;
- Знать, что такое осевое сечение цилиндра;
- Знать формулу объема цилиндра;
- Знать, что такое развертка боковой поверхности цилиндра и чему равна ее площадь;
- Уметь находить полную площадь боковой поверхности прямого цилиндра, объем цилиндра.
- Какой многогранник называется пирамидой?
- Что такое призма?
- Какие составные элементы пирамиды вы знаете?
- Какая пирамида называется правильной?
- Что такое апофема правильной пирамиды?
- Чему равна площадь боковой поверхности правильной пирамиды?
- Как найти площадь полной поверхности пирамиды?
- Чему равна площадь круга? Длина окружности?
Тела и поверхности вращения. Цилиндр
Тело, образуемое вращением какой-нибудь плоской фигуры около неподвижной прямой линии, называется телом вращения. Неподвижная прямая называется осью вращения.
Вырежем из картона прямоугольник и насадим его на ось и будем очень быстро вращать вокруг этой оси. Наш глаз примерно в течении секунды удерживает зрительное впечатление. Поэтому, если прямоугольник будет делать 15-20 оборотов в секунду, мы перестанем различать отдельные его положения, а увидим сплошное круглое тело.
Цилиндр – фигура, полученная вращением прямоугольника вокруг одной из его сторон.
 Рис. 1. Цилиндр
Рис. 1. Цилиндр
На рисунке 1 цилиндр, полученный вращением прямоугольника вокруг одной из его сторон или прямоугольника вокруг прямой , которая проходит через серединные точки противолежащих сторон.
Прямая называется осью цилиндра, отрезки и – образующие цилиндра. В качестве высоты цилиндра можно выбрать любой из отрезков . Два круга, лежащих в параллельных плоскостях, которые образовались при вращении, называют основаниями цилиндра. Радиус цилиндра – это радиус его основания .
При вращении стороны , образуется поверхность, состоящая из множества отрезков (образующих цилиндра), параллельных оси цилиндра. Ее называют цилиндрической или боковой поверхностью.
Таким образом, цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра является прямоугольник (рис. 1).
Тела, имеющие форму цилиндра, встречаются довольно часто. Оси колес, стержни, валы, колонны, столбы, обтесанные бревна и многие другие предметы имеют форму цилиндра. Например, трубы, банки, стаканы, ведра имеют форму цилиндра, пустого внутри.
Объем цилиндра равен произведению площади основания на высоту
,
где – объем цилиндра, – площадь основания, - высота цилиндра.
Так как основанием цилиндра является круг, а его площадь равна , то объем цилиндра также можно вычислить по формуле:
.
Пример 1
Найдите объем цилиндра, если диаметр его основания равен 12 см, а высота равна 5 см .
Решение
Сначала найдем радиус основания, как половину диаметра:
см.
Найдем объем цилиндра по формуле :
см3.
Ответ: 565,2 см3.
На рисунке 2 изображен цилиндр. Представьте себе,что его боковую часть разрезали по образующей и развернули таким образом, что получился прямоугольник. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Длина данного прямоугольника равна длине окружности основания, а ширина равна высоте цилиндра. Таким образом, легко получить формулу для вычисления площади боковой поверхности цилиндра.
 Рис. 2. Развёртка боковой поверхности цилиндра
Рис. 2. Развёртка боковой поверхности цилиндра
Площадь боковой поверхности цилиндра равна площади ее развертки и находится по формуле:
.
Площадь полной поверхности прямого цилиндра состоит из двух равных площадей оснований и площади боковой поверхности. Таким образом:
.
Пример 2
Точки и – центры оснований цилиндра, – радиус основания, – образующая цилиндра. Найдите площадь боковой поверхности и объем цилиндра, если см, см .
Решение
Радиус основания цилиндра см, будет являться высотой, т.е. см.
Найдем площадь боковой поверхности по формуле:
см2
2. Найдем объем по формуле:
см3
Ответ: 113,04 см2, 169,56 см3.
Упражнение 1
1. Найдите объем цилиндра, если диаметр его основания равен 20 см, а высота равна 12 см .
2. Точки и – центры оснований цилиндра, – радиус основания. Найдите площадь боковой поверхности и объем цилиндра, если см, см .
Контрольные вопросы
1. Объясните, какое тело называется цилиндром?
2. Объясните, что такое цилиндрическая поверхность?
3. По какой формуле можно найти объем цилиндра?
4. Как вычислить площадь боковой поверхности цилиндра?
Упражнение 1
1. 3768 см3;
2. 226,08 см2, 452,16 см3.



