- Импульс. Изменение импульса материальной точки
- Система тел. Импульс системы тел
- Закон сохранения импульса
- знать понятия и формулы импульса материальной точки и импульса силы; понятие системы тел; формулировку закона изменения импульса материальной точки; закон сохранения импульса
- уметь отличать внутренние и внешние силы; находить импульс системы тел
- По какой формуле рассчитывается ускорение тела?
- Как определить характер движения тел, если неизвестны силы, действующие на тело?
- Как изменяется скорость тела, если на него начинает действовать постоянная сила?
Импульс. Изменение импульса материальной точки
Законы Ньютона позволяют определить характер движения тела, если известны силы, действующие на материальную точку. В случае, если действующие силы неизвестны, применяются закон сохранения импульса и закон сохранения энергии.
Любое тело, обладающее массой и скоростью, имеет импульс , модуль которого равен:
,
где — масса тела;
— скорость тела;
— импульс тела.
Импульс тела — это физическая величина, равная произведению массы на скорость: .
Импульс — векторная физическая величина, направление вектора совпадает с направлением вектора скорости :
.
В СИ единицей измерения импульса является килограмм-метр в секунду (кг ∙ м/с).
Понятно, что изменение импульса материальной точки напрямую связано с изменением скорости , следовательно, и с ускорением тела .
По определению ускорение находится по следующей формуле:
.
Согласно второму закону Ньютона ускорение тела есть отношение силы, действующей на тело, к массе этого тела:
.
Объединим эти формулы и выразим силу F:
.
Таким образом, изменение импульса равно:
или .
Данное выражение называется законом изменения импульса материальной точки в инерциальной системе отсчёта или вторым законом Ньютона в импульсной форме.
В инерциальной системе отсчёта изменение импульса Δp материальной точки за промежуток времени Δt равно произведению суммы всех сил F, действующих на тело за данный промежуток времени: .
Произведение представляет собой импульс суммы всех сил, действующих на материальную точку, и называется импульсом силы.
Формула изменения импульса предполагает, что сумма всех сил F в течение времени Δt не изменяется. В противном случае промежуток времени Δt разбивают на такое количество промежутков, чтобы значение силы F можно было считать постоянным. Для каждого такого промежутка времени рассчитывается изменение импульса. Суммарное изменение импульса тела рассчитывается как сумма всех импульсов сил за рассматриваемые промежутки времени:
.
Система тел. Импульс системы тел
Использование второго закона Ньютона в импульсной форме позволяет упростить решение задач на движение нескольких взаимодействующих тел.
Пусть необходимо выяснить, как будут двигаться два бильярдных шара после столкновения. Силы, с которыми шары подействовали друг на друга в момент удара, неизвестны. Несмотря на это, выражение изменения импульса даёт возможность описать движение данных тел.
Прежде всего, рассматриваемые тела следует объединить в систему тел. При объединении нескольких тел в систему все силы, приложенные к телам, разделяются на внутренние и внешние.
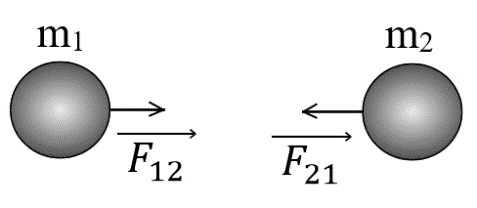 Рис. 1. Система, состоящая из двух тел
Рис. 1. Система, состоящая из двух тел
Например, на рисунке 1 изображены два бильярдных шара перед столкновением. В момент удара шар массой m1 подействует на шар массой m2 с силой , шар массой m2, в свою очередь, подействует на шар массой m1 с силой . Силы и являются внутренними. В то же время на тела будут действовать силы тяжести и , силы реакции опоры и , а также силы трения и о поверхность — это внешние силы, так как поверхность стола и Земля не входят в выбранную систему тел.
Силы взаимодействия между телами, принадлежащими системе, называются внутренними силами.
Силы, действующие на тела системы со стороны тел, не входящих в систему, называются внешними силами.
 Рис. 2. Внешние и внутренние силы, действующие на систему тел
Рис. 2. Внешние и внутренние силы, действующие на систему тел
Внешние силы обозначают индексом «ex». Пусть сума всех внешних сил, действующих на шар массой m1, равна , на шар массой m2 — (рис. 2).
Тогда на первый шар действуют силы и , на второй шар — силы и .
В соответствии с введёнными обозначениями изменения импульсов шаров за время Δt равны:
;
.
Импульсом системы тел называется сумма импульсов всех тел, входящих в рассматриваемую систему: .
В нашем случае в систему входят только два тела, следовательно, суммарный импульс системы равен
.
Изменение импульса системы тел равно сумме изменений импульсов каждого тела, входящего в систему:
.
Подставим в формулу изменения импульса выражения:
.
Так как силы и , с которыми взаимодействуют между собой бильярдные шары, по третьему закону Ньютона равны по модулю и противоположны по направлению, их сумма будет равна нулю . Тогда выражение выше принимает следующий вид:
.
Закон изменения импульса системы тел: изменение импульса системы тел в инерциальной системе отсчёта равно произведению постоянной суммы всех внешних сил на время их действия: .
Закон сохранения импульса
Если сумма внешних сил равна нулю , изменение импульса данной системы также равно нулю .
Данное утверждение называется законом сохранения импульса.
Закон сохранения импульса: если сумма всех внешних сил, действующих на тела, входящие в систему, равна нулю, то импульс системы тел в инерциальной системе отсчёта остаётся постоянным с течением времени.
При решении задач удобно использовать следующую формулировку закона сохранения импульса: если сумма внешних сил равна нулю, то начальный импульс системы равен конечному импульсу данной системы:
.
Для системы из n тел закон сохранения импульса будет иметь следующий вид:
.
При решении задач выражение выше записывают в проекциях на координатные оси:
;
.
В некоторых случаях сохраняется проекция импульса системы тел на одну из координатных осей, а проекция на другую ось изменяется.
Запишем уравнение в проекциях на координатные оси:
.
В случае, если , проекция изменения импульса системы также равна нулю . При этом проекция изменения импульса системы на ось ординат, а значит и вектор , могут оказаться отличными от нуля.
Закон сохранения проекции импульса на координатную ось: если проекция на координатную ось суммы всех внешних сил, действующих на тела системы, равна нулю, то проекция импульса системы тел на данную ось остаётся постоянной с течением времени.
Итоги
- Импульс тела — это физическая величина, равная произведению массы на скорость: .
- В инерциальной системе отсчёта изменение импульса Δp материальной точки за промежуток времени Δt равно произведению суммы всех сил F, действующих на тело, на данный промежуток времени: . Произведение называется импульсом силы.
- Импульсом системы тел называется сумма импульсов всех тел, входящих в рассматриваемую систему: .
- Закон изменения импульса системы тел: изменение импульса системы тел в инерциальной системе отсчёта равно произведению постоянной суммы всех внешних сил на время их действия: .
- Закон сохранения импульса: если сумма всех внешних сил, действующих на тела, входящие в систему, равна нулю, то импульс системы тел в инерциальной системе отсчёта остаётся постоянным с течением времени: .
Контрольные вопросы
1. Дайте определение импульса материальной точки.
2. Какие силы называются внешними, а какие внутренними? Приведите пример.
3. Сформулируйте закон сохранения импульса.
- Импульс. Изменение импульса материальной точки
- Система тел. Импульс системы тел
- Закон сохранения импульса
- знать понятия и формулы импульса материальной точки и импульса силы; понятие системы тел; формулировку закона изменения импульса материальной точки; закон сохранения импульса
- уметь отличать внутренние и внешние силы; находить импульс системы тел
- По какой формуле рассчитывается ускорение тела?
- Как определить характер движения тел, если неизвестны силы, действующие на тело?
- Как изменяется скорость тела, если на него начинает действовать постоянная сила?
Импульс. Изменение импульса материальной точки
Законы Ньютона позволяют определить характер движения тела, если известны силы, действующие на материальную точку. В случае, если действующие силы неизвестны, применяются закон сохранения импульса и закон сохранения энергии.
Любое тело, обладающее массой и скоростью, имеет импульс , модуль которого равен:
,
где — масса тела;
— скорость тела;
— импульс тела.
Импульс тела — это физическая величина, равная произведению массы на скорость: .
Импульс — векторная физическая величина, направление вектора совпадает с направлением вектора скорости :
.
В СИ единицей измерения импульса является килограмм-метр в секунду (кг ∙ м/с).
Понятно, что изменение импульса материальной точки напрямую связано с изменением скорости , следовательно, и с ускорением тела .
По определению ускорение находится по следующей формуле:
.
Согласно второму закону Ньютона ускорение тела есть отношение силы, действующей на тело, к массе этого тела:
.
Объединим эти формулы и выразим силу F:
.
Таким образом, изменение импульса равно:
или .
Данное выражение называется законом изменения импульса материальной точки в инерциальной системе отсчёта или вторым законом Ньютона в импульсной форме.
В инерциальной системе отсчёта изменение импульса Δp материальной точки за промежуток времени Δt равно произведению суммы всех сил F, действующих на тело за данный промежуток времени: .
Произведение представляет собой импульс суммы всех сил, действующих на материальную точку, и называется импульсом силы.
Формула изменения импульса предполагает, что сумма всех сил F в течение времени Δt не изменяется. В противном случае промежуток времени Δt разбивают на такое количество промежутков, чтобы значение силы F можно было считать постоянным. Для каждого такого промежутка времени рассчитывается изменение импульса. Суммарное изменение импульса тела рассчитывается как сумма всех импульсов сил за рассматриваемые промежутки времени:
.
Система тел. Импульс системы тел
Использование второго закона Ньютона в импульсной форме позволяет упростить решение задач на движение нескольких взаимодействующих тел.
Пусть необходимо выяснить, как будут двигаться два бильярдных шара после столкновения. Силы, с которыми шары подействовали друг на друга в момент удара, неизвестны. Несмотря на это, выражение изменения импульса даёт возможность описать движение данных тел.
Прежде всего, рассматриваемые тела следует объединить в систему тел. При объединении нескольких тел в систему все силы, приложенные к телам, разделяются на внутренние и внешние.
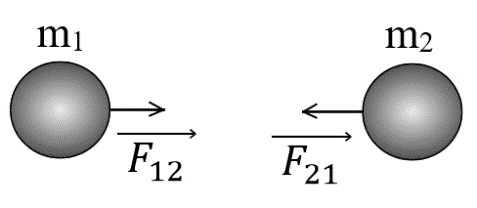 Рис. 1. Система, состоящая из двух тел
Рис. 1. Система, состоящая из двух тел
Например, на рисунке 1 изображены два бильярдных шара перед столкновением. В момент удара шар массой m1 подействует на шар массой m2 с силой , шар массой m2, в свою очередь, подействует на шар массой m1 с силой . Силы и являются внутренними. В то же время на тела будут действовать силы тяжести и , силы реакции опоры и , а также силы трения и о поверхность — это внешние силы, так как поверхность стола и Земля не входят в выбранную систему тел.
Силы взаимодействия между телами, принадлежащими системе, называются внутренними силами.
Силы, действующие на тела системы со стороны тел, не входящих в систему, называются внешними силами.
 Рис. 2. Внешние и внутренние силы, действующие на систему тел
Рис. 2. Внешние и внутренние силы, действующие на систему тел
Внешние силы обозначают индексом «ex». Пусть сума всех внешних сил, действующих на шар массой m1, равна , на шар массой m2 — (рис. 2).
Тогда на первый шар действуют силы и , на второй шар — силы и .
В соответствии с введёнными обозначениями изменения импульсов шаров за время Δt равны:
;
.
Импульсом системы тел называется сумма импульсов всех тел, входящих в рассматриваемую систему: .
В нашем случае в систему входят только два тела, следовательно, суммарный импульс системы равен
.
Изменение импульса системы тел равно сумме изменений импульсов каждого тела, входящего в систему:
.
Подставим в формулу изменения импульса выражения:
.
Так как силы и , с которыми взаимодействуют между собой бильярдные шары, по третьему закону Ньютона равны по модулю и противоположны по направлению, их сумма будет равна нулю . Тогда выражение выше принимает следующий вид:
.
Закон изменения импульса системы тел: изменение импульса системы тел в инерциальной системе отсчёта равно произведению постоянной суммы всех внешних сил на время их действия: .
Закон сохранения импульса
Если сумма внешних сил равна нулю , изменение импульса данной системы также равно нулю .
Данное утверждение называется законом сохранения импульса.
Закон сохранения импульса: если сумма всех внешних сил, действующих на тела, входящие в систему, равна нулю, то импульс системы тел в инерциальной системе отсчёта остаётся постоянным с течением времени.
При решении задач удобно использовать следующую формулировку закона сохранения импульса: если сумма внешних сил равна нулю, то начальный импульс системы равен конечному импульсу данной системы:
.
Для системы из n тел закон сохранения импульса будет иметь следующий вид:
.
При решении задач выражение выше записывают в проекциях на координатные оси:
;
.
В некоторых случаях сохраняется проекция импульса системы тел на одну из координатных осей, а проекция на другую ось изменяется.
Запишем уравнение в проекциях на координатные оси:
.
В случае, если , проекция изменения импульса системы также равна нулю . При этом проекция изменения импульса системы на ось ординат, а значит и вектор , могут оказаться отличными от нуля.
Закон сохранения проекции импульса на координатную ось: если проекция на координатную ось суммы всех внешних сил, действующих на тела системы, равна нулю, то проекция импульса системы тел на данную ось остаётся постоянной с течением времени.
Итоги
- Импульс тела — это физическая величина, равная произведению массы на скорость: .
- В инерциальной системе отсчёта изменение импульса Δp материальной точки за промежуток времени Δt равно произведению суммы всех сил F, действующих на тело, на данный промежуток времени: . Произведение называется импульсом силы.
- Импульсом системы тел называется сумма импульсов всех тел, входящих в рассматриваемую систему: .
- Закон изменения импульса системы тел: изменение импульса системы тел в инерциальной системе отсчёта равно произведению постоянной суммы всех внешних сил на время их действия: .
- Закон сохранения импульса: если сумма всех внешних сил, действующих на тела, входящие в систему, равна нулю, то импульс системы тел в инерциальной системе отсчёта остаётся постоянным с течением времени: .
Контрольные вопросы
1. Дайте определение импульса материальной точки.
2. Какие силы называются внешними, а какие внутренними? Приведите пример.
3. Сформулируйте закон сохранения импульса.



