- Усечённая пирамида
- Знать, какая фигура называется усечённой пирамидой;
- Знать, какая усечённая пирамида называется правильной;
- Знать и уметь доказывать теорему о площади боковой поверхности усечённой пирамиды.
- Что такое пирамида?
- Какую пирамиду называют правильной?
- Какую фигуру на плоскости называют трапецией?
- Что называют расстоянием между плоскостями?
Усечённая пирамида
Усечённая пирамида — часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.
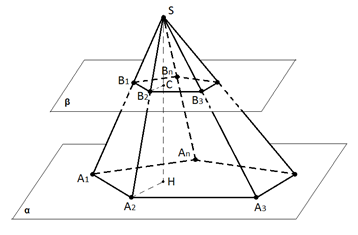
На рисунке 1 изображена пирамида , основание которой лежит в плоскости . Плоскость , параллельная плоскости , пересекает боковые рёбра пирамиды в точках и разбивает пирамиду на два многогранника. Один из многогранников заключён между основанием , боковыми гранями исходной пирамиды и многоугольником .
Этот многогранник является усечённой пирамидой и обозначается .
 1A2A3…AnB1B2B3…Bn" loading="lazy" />
Рис. 1. Усечённая пирамида A1A2A3…AnB1B2B3…Bn
1A2A3…AnB1B2B3…Bn" loading="lazy" />
Рис. 1. Усечённая пирамида A1A2A3…AnB1B2B3…Bn
Многоугольники и называются основаниями усечённой пирамиды.
Многоугольники , , …, называются боковыми гранями усечённой пирамиды.
Отрезки , , …, называются боковыми рёбрами усечённой пирамиды.
На рисунке также показана высота исходной пирамиды и высота усечённой пирамиды.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды.
Боковые грани усечённой пирамиды являются трапециями. Докажем, например, что боковая грань – трапеция (рис. 1). Стороны и параллельны, так как лежат на прямых, по которым плоскость пересекается с параллельными плоскостями и . Другие две стороны и этой грани не параллельны, поскольку прямые, которым принадлежат эти стороны, пересекаются в точке S. Таким образом, в четырёхугольнике две противоположные стороны параллельны, а две другие стороны не параллельны. Значит, – трапеция. Аналогично доказывается, что и остальные грани – трапеции.
Введём понятие правильной усечённой пирамиды.
Правильной усеченной пирамидой называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.
Основания усечённой пирамиды – правильные многоугольники, а боковые грани – равные между собой равнобедренные трапеции. Высоты этих трапеций называются апофемами.
Теорема
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Доказательство
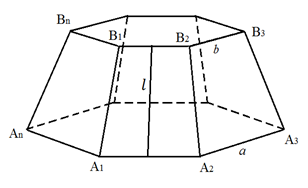 Рис. 2. К доказательству теоремы 1
Рис. 2. К доказательству теоремы 1
Боковые грани правильной усечённой пирамиды – равные между собой равнобедренные трапеции с одним и тем же верхним основанием , нижним и высотой (апофемой) (рис. 2). Поэтому площадь одной грани равна Площадь всех граней, т. е. боковая поверхность, равна , где
– число вершин у оснований пирамиды, и – периметры оснований пирамиды.
Теорема доказана.
Пример 1
Высота правильной четырёхугольной усечённой пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды.
Решение
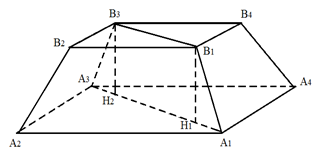 Рис. 3. К примеру 1
Рис. 3. К примеру 1
Пусть квадраты и являются основаниями правильной четырёхугольной усечённой пирамиды (рис. 3).
По условию , .
Диагональное сечение этой призмы является равнобедренной трапецией с основаниями и .
Найдём эти основания.
,
.
По условию высота пирамиды равна 7 см. Значит, в прямоугольном треугольнике катет равен 7 см. Найдём катет .
.
Найдём теперь боковое ребро усечённой пирамиды, которое является гипотенузой прямоугольного треугольника .
.
Ответ: 9 см.
Пример 2
Стороны оснований правильной усечённой треугольной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
Решение
 Рис. 4. К примеру 2
Рис. 4. К примеру 2
Центры оснований и правильной усечённой треугольной пирамиды (рис. 4) делят медианы оснований и в отношении 2:1 считая от вершин и . Отрезок является высотой пирамиды.
Найдём сначала медианы равносторонних треугольников и (они также являются и высотами этих треугольников).
;
.
Теперь найдём отрезки и .
;
.
Рассмотрим прямоугольную трапецию . Проведём высоту .
.
.
По условию .
Тогда по теореме Пифагора получим
.
Таким образом, мы нашли высоту усечённой пирамиды .
Ответ: 1 дм.
Упражнение 1
1. В правильной усеченной четырёхугольной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Найдите диагональ этой пирамиды.
2. Стороны оснований усечённой правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60o. Найдите высоту.
3. Высота правильной четырёхугольной усечённой пирамиды равна 4 см. Стороны оснований равны 2 см и 8 см. Найдите площади диагональных сечений.
4. В правильной четырёхугольной усечённой пирамиде стороны оснований 8 м и 2 м. Высота пирамиды равна 4 м. Найдите площадь полной поверхности.
Контрольные вопросы
- Сформулируйте определение усечённой пирамиды.
- Какая усечённая пирамида называется правильной?
- Сформулируйте и докажите теорему о площади боковой поверхности правильной усечённой пирамиды.
Упражнение 1
- 6 см;
- 2 см;
- см2;
- 168 м2.
- Усечённая пирамида
- Знать, какая фигура называется усечённой пирамидой;
- Знать, какая усечённая пирамида называется правильной;
- Знать и уметь доказывать теорему о площади боковой поверхности усечённой пирамиды.
- Что такое пирамида?
- Какую пирамиду называют правильной?
- Какую фигуру на плоскости называют трапецией?
- Что называют расстоянием между плоскостями?
Усечённая пирамида
Усечённая пирамида — часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.
На рисунке 1 изображена пирамида , основание которой лежит в плоскости . Плоскость , параллельная плоскости , пересекает боковые рёбра пирамиды в точках и разбивает пирамиду на два многогранника. Один из многогранников заключён между основанием , боковыми гранями исходной пирамиды и многоугольником .
Этот многогранник является усечённой пирамидой и обозначается .
 1A2A3…AnB1B2B3…Bn" loading="lazy" />
Рис. 1. Усечённая пирамида A1A2A3…AnB1B2B3…Bn
1A2A3…AnB1B2B3…Bn" loading="lazy" />
Рис. 1. Усечённая пирамида A1A2A3…AnB1B2B3…Bn
Многоугольники и называются основаниями усечённой пирамиды.
Многоугольники , , …, называются боковыми гранями усечённой пирамиды.
Отрезки , , …, называются боковыми рёбрами усечённой пирамиды.
На рисунке также показана высота исходной пирамиды и высота усечённой пирамиды.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды.
Боковые грани усечённой пирамиды являются трапециями. Докажем, например, что боковая грань – трапеция (рис. 1). Стороны и параллельны, так как лежат на прямых, по которым плоскость пересекается с параллельными плоскостями и . Другие две стороны и этой грани не параллельны, поскольку прямые, которым принадлежат эти стороны, пересекаются в точке S. Таким образом, в четырёхугольнике две противоположные стороны параллельны, а две другие стороны не параллельны. Значит, – трапеция. Аналогично доказывается, что и остальные грани – трапеции.
Введём понятие правильной усечённой пирамиды.
Правильной усеченной пирамидой называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.
Основания усечённой пирамиды – правильные многоугольники, а боковые грани – равные между собой равнобедренные трапеции. Высоты этих трапеций называются апофемами.
Теорема
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Доказательство
 Рис. 2. К доказательству теоремы 1
Рис. 2. К доказательству теоремы 1
Боковые грани правильной усечённой пирамиды – равные между собой равнобедренные трапеции с одним и тем же верхним основанием , нижним и высотой (апофемой) (рис. 2). Поэтому площадь одной грани равна Площадь всех граней, т. е. боковая поверхность, равна , где
– число вершин у оснований пирамиды, и – периметры оснований пирамиды.
Теорема доказана.
Пример 1
Высота правильной четырёхугольной усечённой пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды.
Решение
 Рис. 3. К примеру 1
Рис. 3. К примеру 1
Пусть квадраты и являются основаниями правильной четырёхугольной усечённой пирамиды (рис. 3).
По условию , .
Диагональное сечение этой призмы является равнобедренной трапецией с основаниями и .
Найдём эти основания.
,
.
По условию высота пирамиды равна 7 см. Значит, в прямоугольном треугольнике катет равен 7 см. Найдём катет .
.
Найдём теперь боковое ребро усечённой пирамиды, которое является гипотенузой прямоугольного треугольника .
.
Ответ: 9 см.
Пример 2
Стороны оснований правильной усечённой треугольной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
Решение
 Рис. 4. К примеру 2
Рис. 4. К примеру 2
Центры оснований и правильной усечённой треугольной пирамиды (рис. 4) делят медианы оснований и в отношении 2:1 считая от вершин и . Отрезок является высотой пирамиды.
Найдём сначала медианы равносторонних треугольников и (они также являются и высотами этих треугольников).
;
.
Теперь найдём отрезки и .
;
.
Рассмотрим прямоугольную трапецию . Проведём высоту .
.
.
По условию .
Тогда по теореме Пифагора получим
.
Таким образом, мы нашли высоту усечённой пирамиды .
Ответ: 1 дм.
Упражнение 1
1. В правильной усеченной четырёхугольной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Найдите диагональ этой пирамиды.
2. Стороны оснований усечённой правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60o. Найдите высоту.
3. Высота правильной четырёхугольной усечённой пирамиды равна 4 см. Стороны оснований равны 2 см и 8 см. Найдите площади диагональных сечений.
4. В правильной четырёхугольной усечённой пирамиде стороны оснований 8 м и 2 м. Высота пирамиды равна 4 м. Найдите площадь полной поверхности.
Контрольные вопросы
- Сформулируйте определение усечённой пирамиды.
- Какая усечённая пирамида называется правильной?
- Сформулируйте и докажите теорему о площади боковой поверхности правильной усечённой пирамиды.
Упражнение 1
- 6 см;
- 2 см;
- см2;
- 168 м2.


