- Пирамида;
- Правильная пирамида.
- Знать, что такое пирамида, правильная пирамида;
- Знать и уметь доказывать теорему о боковой поверхности правильной пирамиды;
- Уметь вычислять площадь боковой и полной поверхности пирамиды.
- Что такое многогранник?
- Какую геометрическую фигуру называют призмой?
- Что такое перпендикуляр к плоскости?
- Какой многоугольник называется правильным?
Пирамида
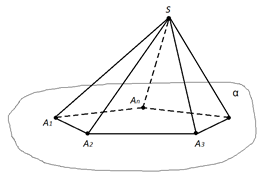 Рис. 1. Пирамида
Рис. 1. Пирамида
Пусть многоугольник лежит в плоскости , а точка не лежит в этой плоскости. Соединим отрезками точку S с вершинами многоугольника . В результате мы получим многогранник, составленный из многоугольника и треугольников , , …, .
Такой многогранник называется пирамидой.
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Общей вершиной этих треугольников является вершина пирамида. Сторона каждого из этих треугольников, противолежащая вершине пирамиды, является стороной основания пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами.
Пирамиду с основанием и вершиной обозначают и называют -угольной пирамидой.
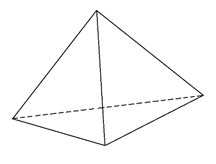 Рис. 2. Треугольная пирамида
Рис. 2. Треугольная пирамида
На рисунке 2 показана треугольная пирамида (тетраэдр), а на рисунке 3 – четырёхугольная пирамида и перпендикуляр , проведённый из вершины пирамиды к плоскости основания пирамиды. Этот перпендикуляр называется высотой пирамиды.
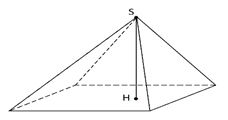 Рис. 3. Четырёхугольная пирамида (SH - высота)
Рис. 3. Четырёхугольная пирамида (SH - высота)
Высотой пирамиды называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
Пример 1
Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
Решение
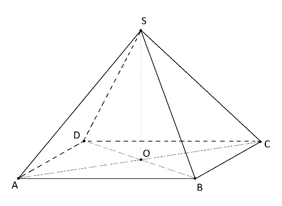 Рис. 4. К примеру 1
Рис. 4. К примеру 1
Пусть – точка пересечения диагоналей основания пирамиды (рис. 4).
, .
Так как по условию боковые рёбра равны, то треугольники и – равнобедренные. При этом основание пирамиды ABCD является прямоугольником. По свойству параллелограмма – середина диагоналей и . Значит – медиана равнобедренных треугольников и , проведённая к их основаниям. Значит, является и высотой этих треугольников.
Таким образом, и . Отсюда следует, что отрезок – перпендикуляр к плоскости основания пирамиды, т. е. – высота пирамиды.
,
,
.
Ответ: 12 см.
Пример 2
Основание пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Все двугранные углы при основании пирамиды равны 60o. Найдите высоту пирамиды.
Решение
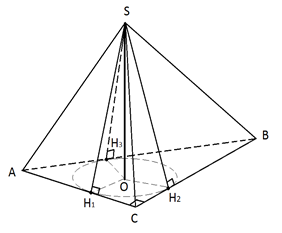 Рис. 5. К примеру 2
Рис. 5. К примеру 2
На рисунке 5 показана пирамида в основании которой лежит прямоугольный треугольник с прямым углом . Проведём высоты боковых граней , , и высоту пирамиды . По условию задачи , – общий катет треугольников , и . Значит, по признаку равенства прямоугольных треугольников эти треугольники равны.
Из равенства треугольников следует, что . При этом , и являются проекциями высот боковых граней на плоскость . Значит, , и . Это означает, что – центр окружности, вписанной в треугольник .
,
,
,
.
Так как треугольник – прямоугольный и , то .
Ответ: .
Правильная пирамида
Перейдём к описанию правильной пирамиды.
Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
У правильной пирамиды боковые рёбра равны. Следовательно, боковые грани – равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
Сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.
Теорема
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
,
где периметр основания, апофема.
Доказательство
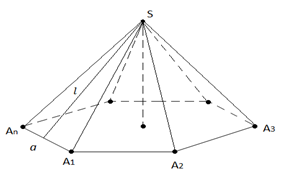 Рис. 6. К доказательству теоремы 1
Рис. 6. К доказательству теоремы 1
Пусть – сторона основания правильной пирамиды;
– число сторон основания (рис. 6). Тогда боковая поверхность пирамиды равна
,
где – апофема, – периметр основания пирамиды.
Теорема доказана.
Пример 3
Найдите сторону основания и апофему правильной треугольной пирамиды, если её боковое ребро равно 10 см, а боковая поверхность равна .
Решение
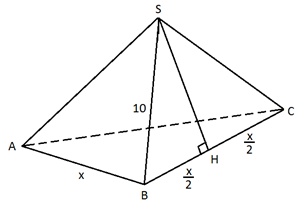 Рис. 7. К примеру 3
Рис. 7. К примеру 3
Сторону основания правильной пирамиды обозначим буквой (рис. 7). Апофема делит сторону основания на отрезки и , равные . Выразим апофему через .
.
Выразим площадь боковой поверхности пирамиды
.
Учитывая, что по условию , получим уравнение
,
,
,
.
Решив данное биквадратное уравнение, получим и .
Таким образом, сторона основания пирамиды равна 16 см или 12 см.
При стороне основания 16 см, апофема равна
.
При стороне основания 12 см, апофема равна
.
Ответ: 16 см и 6 см или 12 см и 8 см.
Упражнение 1
1. В правильной четырёхугольной пирамиде найдите сторону основания, если боковое ребро равно 5 см, а площадь полной поверхности равна .
2. Найдите двугранные углы тетраэдра, все грани которого являются равносторонними треугольниками.
Контрольные вопросы
- Какой многогранник называется пирамидой?
- Какая пирамида называется правильной?
- Что такое апофема?
- Сформулируйте теорему о площади боковой поверхности правильной пирамиды.
Упражнение 1
- .
- .
- Пирамида;
- Правильная пирамида.
- Знать, что такое пирамида, правильная пирамида;
- Знать и уметь доказывать теорему о боковой поверхности правильной пирамиды;
- Уметь вычислять площадь боковой и полной поверхности пирамиды.
- Что такое многогранник?
- Какую геометрическую фигуру называют призмой?
- Что такое перпендикуляр к плоскости?
- Какой многоугольник называется правильным?
Пирамида
 Рис. 1. Пирамида
Рис. 1. Пирамида
Пусть многоугольник лежит в плоскости , а точка не лежит в этой плоскости. Соединим отрезками точку S с вершинами многоугольника . В результате мы получим многогранник, составленный из многоугольника и треугольников , , …, .
Такой многогранник называется пирамидой.
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Общей вершиной этих треугольников является вершина пирамида. Сторона каждого из этих треугольников, противолежащая вершине пирамиды, является стороной основания пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами.
Пирамиду с основанием и вершиной обозначают и называют -угольной пирамидой.
 Рис. 2. Треугольная пирамида
Рис. 2. Треугольная пирамида
На рисунке 2 показана треугольная пирамида (тетраэдр), а на рисунке 3 – четырёхугольная пирамида и перпендикуляр , проведённый из вершины пирамиды к плоскости основания пирамиды. Этот перпендикуляр называется высотой пирамиды.
 Рис. 3. Четырёхугольная пирамида (SH - высота)
Рис. 3. Четырёхугольная пирамида (SH - высота)
Высотой пирамиды называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
Пример 1
Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
Решение
 Рис. 4. К примеру 1
Рис. 4. К примеру 1
Пусть – точка пересечения диагоналей основания пирамиды (рис. 4).
, .
Так как по условию боковые рёбра равны, то треугольники и – равнобедренные. При этом основание пирамиды ABCD является прямоугольником. По свойству параллелограмма – середина диагоналей и . Значит – медиана равнобедренных треугольников и , проведённая к их основаниям. Значит, является и высотой этих треугольников.
Таким образом, и . Отсюда следует, что отрезок – перпендикуляр к плоскости основания пирамиды, т. е. – высота пирамиды.
,
,
.
Ответ: 12 см.
Пример 2
Основание пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Все двугранные углы при основании пирамиды равны 60o. Найдите высоту пирамиды.
Решение
 Рис. 5. К примеру 2
Рис. 5. К примеру 2
На рисунке 5 показана пирамида в основании которой лежит прямоугольный треугольник с прямым углом . Проведём высоты боковых граней , , и высоту пирамиды . По условию задачи , – общий катет треугольников , и . Значит, по признаку равенства прямоугольных треугольников эти треугольники равны.
Из равенства треугольников следует, что . При этом , и являются проекциями высот боковых граней на плоскость . Значит, , и . Это означает, что – центр окружности, вписанной в треугольник .
,
,
,
.
Так как треугольник – прямоугольный и , то .
Ответ: .
Правильная пирамида
Перейдём к описанию правильной пирамиды.
Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
У правильной пирамиды боковые рёбра равны. Следовательно, боковые грани – равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
Сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.
Теорема
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
,
где периметр основания, апофема.
Доказательство
 Рис. 6. К доказательству теоремы 1
Рис. 6. К доказательству теоремы 1
Пусть – сторона основания правильной пирамиды;
– число сторон основания (рис. 6). Тогда боковая поверхность пирамиды равна
,
где – апофема, – периметр основания пирамиды.
Теорема доказана.
Пример 3
Найдите сторону основания и апофему правильной треугольной пирамиды, если её боковое ребро равно 10 см, а боковая поверхность равна .
Решение
 Рис. 7. К примеру 3
Рис. 7. К примеру 3
Сторону основания правильной пирамиды обозначим буквой (рис. 7). Апофема делит сторону основания на отрезки и , равные . Выразим апофему через .
.
Выразим площадь боковой поверхности пирамиды
.
Учитывая, что по условию , получим уравнение
,
,
,
.
Решив данное биквадратное уравнение, получим и .
Таким образом, сторона основания пирамиды равна 16 см или 12 см.
При стороне основания 16 см, апофема равна
.
При стороне основания 12 см, апофема равна
.
Ответ: 16 см и 6 см или 12 см и 8 см.
Упражнение 1
1. В правильной четырёхугольной пирамиде найдите сторону основания, если боковое ребро равно 5 см, а площадь полной поверхности равна .
2. Найдите двугранные углы тетраэдра, все грани которого являются равносторонними треугольниками.
Контрольные вопросы
- Какой многогранник называется пирамидой?
- Какая пирамида называется правильной?
- Что такое апофема?
- Сформулируйте теорему о площади боковой поверхности правильной пирамиды.
Упражнение 1
- .
- .


