Понятие многогранника. Призма

План урока

Понятие многогранника;
Призма.

Цели урока

Знать, что такое многогранник;
Знать определение призмы;
Знать теорему о площади боковой поверхности призмы и уметь её доказывать;
Уметь применять теорему о площади боковой поверхности призмы при решении задач.

Разминка

Какую геометрическую фигуру называют тетраэдром?
Какую геометрическую фигуру называют параллелепипедом?
Какие прямые в пространстве называются параллельными?
Какие плоскости называются параллельными?

Понятие многогранника

Многогранник – это геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.

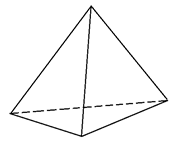Рис. 1. Тетраэдр

Вам уже знакомы два вида многогранников.

Тетраэдр – многогранник, составленный из четырёх треугольников (рис. 1).

Параллелепипед – многогранник, составленный из шести параллелограммов (рис. 2).

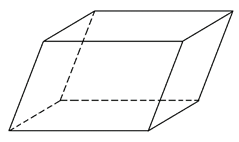Рис. 2. Параллелепипед

Многоугольники, из которых составлен многогранник, называются его гранями. Гранями тетраэдра являются треугольники, гранями параллелепипеда – параллелограммы.

Стороны граней называют рёбрами, а концы рёбер – вершинами многогранника.

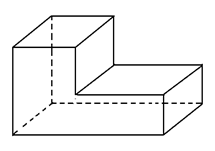Рис. 3. Невыпуклый многогранник

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью , а общая часть многогранника и секущей плоскости – сечением многогранника.

Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой грани.

Например, тетраэдр и параллелепипед являются выпуклыми многогранниками, а многогранник, изображённый на рисунке 3 – невыпуклый многогранник.

Все грани выпуклого многогранника являются выпуклыми многоугольниками.

В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше $360 °$ .

Призма

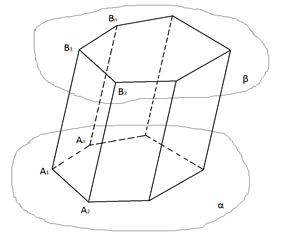Рис. 4. Призма

Пусть в параллельных плоскостях $α$ и $β$ расположены два равных многоугольника $A_{1} A_{2} \dots A_{n}$ и $B_{1} B_{2} . . . B_{n}$ таким образом, что отрезки $A_{1} B_{1}$ , $A_{2} B_{2}$ , …, $A_{n} B_{n}$ параллельны (рис. 4).

Так как в каждом из четырёхугольников $A_{1} A_{2} B_{2} B_{1}$ , $A_{2} A_{3} B_{3} B_{2}$ , …, $A_{n} A_{1} B_{1} B_{n}$ противоположные стороны попарно параллельны, то каждый из них является параллелограммом.

Многогранник, составленный из двух равных многоугольников $A_{1} A_{2} \dots A_{n}$ и $B_{1} B_{2} . . . B_{n}$ , расположенных в параллельных плоскостях, и $n$ параллелограммов $A_{1} A_{2} B_{2} B_{1}$ , $A_{2} A_{3} B_{3} B_{2}$ , …, $A_{n} A_{1} B_{1} B_{n}$ , называется призмой .

Многоугольники $A_{1} A_{2} \dots A_{n}$ и $B_{1} B_{2} . . . B_{n}$ называются основаниями, а параллелограммы $A_{1} A_{2} B_{2} B_{1}$ , $A_{2} A_{3} B_{3} B_{2}$ , …, $A_{n} A_{1} B_{1} B_{n}$ – боковыми гранями призмы. Отрезки $A_{1} B_{1}$ , $A_{2} B_{2}$ , …, $A_{n} B_{n}$ называются боковыми рёбрами призмы.

Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в параллельных плоскостях, и всех отрезков, соединяющих соответствующие точки этих многоугольников.

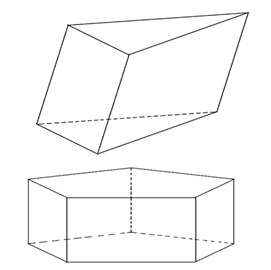Рис. 5. Примеры призм

Если в основании призмы лежит многоугольник с n вершинами ( $n$ -угольник), то призму называют
$n$ -угольной призмой.

Перпендикуляр, проведённый из точки, лежащей в плоскости одного основания, к плоскости другого основания, называется высотой.

На рисунке 5 изображены треугольная и пятиугольная призмы. Пятиугольная призма на данном рисунке является прямой , а треугольная – наклонной . Прямоугольный параллелепипед, который мы рассматривали ранее, также является примером прямой четырёхугольной призмы.

Призма, у которой боковое ребро перпендикулярно к основаниям, называется прямой , в противном случае – наклонной . Заметим, что высота прямой призмы равна её боковому ребру.

Прямая призма называется правильной , если её основания – правильные многоугольники.

Часто возникает необходимость вычислять площадь боковой поверхности призмы (сумму площадей её боковых граней) и площадь полной поверхности призмы (сумму площадей всех её граней). Площадь полной поверхности призмы находится по следующей формуле:

$S_{п о л н} = 2 S_{о с н} + S_{б о к}$

Сформулируем и докажем теорему о площади боковой поверхности прямой призмы.

Теорема

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Доказательство

Боковые грани прямой призмы – прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых рёбер. Следовательно, площадь боковой поверхности призмы равна $S_{б о к} = a_{1} \cdot h + a_{2} \cdot h + \dots + a_{n} \cdot h = h \cdot (a_{1} + a_{2} + \dots + a_{n}) = P \cdot h$ , где $a_{1}, a_{2}, \dots, a_{n}$ – длины рёбер основания, $h$ – длина боковых рёбер, т.е. высота прямой призмы, $P$ – периметр основания призмы.

Теорема доказана.

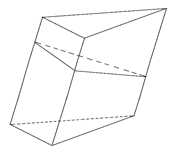Рис. 6.

Пример 1

В наклонной призме проведено сечение, перпендикулярное боковым рёбрам и пересекающее все боковые грани. Найдите боковую поверхность призмы, если периметр сечения равен $ρ$ , а боковые рёбра равны $l$ .

Решение

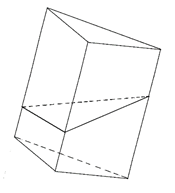Рис. 7.

Плоскость проведённого сечения разбивает призму на две части (рис. 6).

Одну из них перенесём таким образом, чтобы совместились основания прошлой призмы, а сечение будет в роли нижнего основания новой призмы (рис. 7). В результате этого получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые рёбра равны (боковое ребро прямой призмы равно высоте призмы). При этом боковая поверхность этой прямой призмы равна боковой поверхности исходной призмы, так как состоит из таких же частей. Следовательно, боковая поверхность исходной призмы равна $p l$ .

Ответ: $S_{б о к} = p l$ .

Пример 2

Рис. 8. К примеру 2

Боковая поверхность правильной четырёхугольной призмы 32 м², а полная поверхность 40 м². Найдите высоту.

Решение

$S_{о с н} = \frac{S_{п о л н} - S_{б о к}}{2} = \frac{40 - 32}{2} = 4 м^{2}$

Основанием данной призмы является квадрат.

Значит ребро основания равно $2 м$ ,

$S_{б о к} = 4 a h \Rightarrow h = \frac{S_{б о к}}{4 a} = \frac{32}{4 \cdot 2} = 4 м$ .

Ответ: $4 м$ .

Упражнение 1

1. В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см. Найдите площадь сечения, проведённого через боковое ребро и меньшую высоту основания.

2. В прямой треугольной призме все рёбра равны. Боковая поверхность равна 12 м². Найдите высоту.

3. В правильной четырёхугольной призме площадь основания равна 144 см², а высота 14 см. Найдите диагональ призмы.

Контрольные вопросы

Что такое многогранник?
Что такое грань многогранника, ребро, вершина?
Что такое призма?
Какая призма называется прямой, правильной?
Сформулируйте теорему о площади боковой поверхности прямой призмы.

Ответы

Упражнение 1

144 см².
2 м.
22 см.

Конспект урока: Понятие многогранника. Призма

Призма

Понятие многогранника

Призма