Конспект урока: Сложение движений. Преобразования Галилея

Сложение движений. Преобразования Галилея

План урока

Относительность движения. Сложение движений. Преобразования Галилея
Законы движения тела в разных системах отсчёта
Задача об относительном движении двух тел

Цели урока

знать правила сложения скоростей и перемещений
уметь применять правила сложения скоростей и перемещений при решении задач

Разминка

Как найти перемещение человека, идущего по вагону движущегося поезда?
Как изменится ваша скорость относительно платформы метро, если попытаться идти вверх по эскалатору, движущемуся вниз?
Как найти скорость сближения двух тел?

Относительность движения. Сложение движений. Преобразования Галилея

Скорость одного и того же тела относительно разных тел отсчёта может быть различной. Например, человек, находящийся в движущейся лодке, будет иметь разную скорость относительно лодки и относительно берега.

По-разному будет изменяться и координата тела в разных системах отсчёта: в приведённом примере координата человека, сидящего на палубе, относительно лодки остаётся постоянной с течением времени, но будет изменяться относительно берега.

Скорость, перемещение и законы движения тела зависят от выбора системы отсчёта.

Поясним сказанное на конкретном примере.

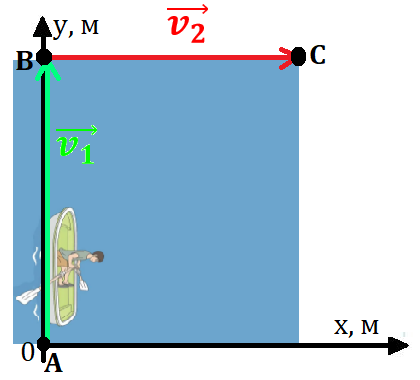Рис. 1. Движение лодки в подвижной воде

Пусть человек на лодке переплывает реку, в которой есть течение, скорость которого равна

v_{2}

. Скорость лодки относительно воды равна

v_{1}

(рис. 1).

Рассмотрим движение человека в двух системах отсчёта: относительно берега и относительно подвижной воды. Система отсчёта, которая находится в покое относительно Земли, называется лабораторной.

Система отсчёта, связанная с водой, называется движущейся, так как она имеет некоторую скорость относительно лабораторной системы отсчёта.

За начало отсчёта обеих систем выберем точку А, из которой человек на лодке начинает движение. Координатные оси направим так, как показано на рисунке 1.

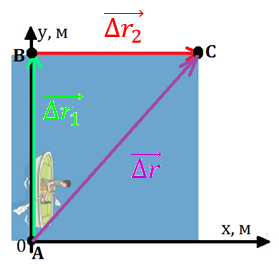Рис. 2. Перемещение человека относительно берега Δr есть сумма векторов Δr<sub loading=

1 и Δr₂" loading="lazy" /> Рис. 2. Перемещение человека относительно берега Δr есть сумма векторов Δr₁ и Δr₂

Пусть человек оказывается на другом берегу через некоторое время Δt. Переправляясь через реку, человек в лодке совершит перемещение ${∆ \vec{r}}_{1}$ относительно движущейся системы отсчёта — воды. С другой стороны, за время Δt точка А воды совершает перемещение ${∆ \vec{r}}_{2}$ относительно лабораторной системы отсчёта — неподвижного берега. Перемещение человека относительно берега $∆ \vec{r}$ представляет собой результат сложения двух движений: движения лодки относительно воды ${∆ \vec{r}}_{1}$ и движения самой воды ${∆ \vec{r}}_{2}$ (рис. 2):

$∆ \vec{r} = {∆ \vec{r}}_{1} + {∆ \vec{r}}_{2}$ .

Движение человека в лодке относительно берега есть сумма движения лодки относительно воды и движения воды относительно неподвижного берега.

Разделим обе части уравнения на достаточно малый промежуток времени Δt:

$\frac{∆ \vec{r}}{∆ t} = \frac{{∆ \vec{r}}_{1}}{∆ t} + \frac{{∆ \vec{r}}_{2}}{∆ t}$ .

Отношение вектора перемещения к достаточно малому промежутку времени Δt представляет собой мгновенную скорость:

$\vec{v} = {\vec{v}}_{1} + {\vec{v}}_{2}$ ,

где $\vec{v}$ — скорость лодки относительно берега;
${\vec{v}}_{1}$ — скорость лодки относительно воды;
${\vec{v}}_{2}$ — скорость воды относительно берега.

Выражения выше называются преобразованиями Галилея.

Закон сложения перемещений: перемещение тела относительно неподвижной системы отсчёта $∆ \vec{r}$ равно сумме вектора перемещения данного тела в подвижной системе отсчёта ${∆ \vec{r}}_{1}$ и вектора перемещения подвижной системы отсчёта ${∆ \vec{r}}_{2}$ : $∆ \vec{r} = {∆ \vec{r}}_{1} + {∆ \vec{r}}_{2}$ .

Закон сложения скоростей: вектор скорости тела относительно неподвижной системы отсчёта

\vec{v}

равен сумме вектора скорости данного тела в подвижной системе отсчёта

{\vec{v}}_{1}

и вектора скорости подвижной системы отсчёта

{\vec{v}}_{2}

\vec{v} = {\vec{v}}_{1} + {\vec{v}}_{2}

Если системы координат лабораторной и движущейся системы отсчёта параллельны друг другу, то преобразования Галилея можно записать в виде проекций перемещений и скоростей:

$∆ x = ∆ x_{1} + ∆ x_{2}$ , $∆ y = ∆ y_{1} + ∆ y_{2}$ ;

$v_{x} = v_{1 x} + v_{2 x}$ , $v_{y} = v_{1 y} + v_{2 y}$ .

Законы движения тела в разных системах отсчёта

Пусть по прямолинейной железной дороге равномерно движется поезд со скоростью $v_{2}$ (рис. 3). По вагону движется человек в направлении движения поезда, скорость человека равна $v_{1}$ .

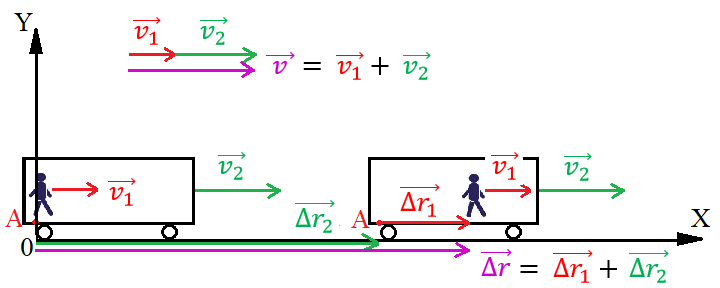Рис. 3. Сложение движений человека относительно поезда и поезда относительно Земли

Человека будем считать точечным телом. Выберем две системы отсчёта: лабораторную, связанную с Землёй, и движущуюся, связанную с поездом. За начало отсчёта обеих систем отсчёта выберем участок железной дороги, над которым находился человек в момент начала наблюдения. Координатные оси направим так, как показано на рисунке.

Рассмотрим движение человека в системе отсчёта, связанной с поездом. Начальная координата человека равна нулю x₀₁ = 0. Человек равномерно движется в положительном направлении оси ОХ со скоростью ${\vec{v}}_{1}$ . Следовательно, проекция скорости человека на ось абсцисс положительна. За промежуток времени t проекция его перемещения на ось ОХ равна $∆ x_{1} = v_{1} \cdot t$ . Закон движения человека в движущейся системе отсчёта будет иметь следующий вид:

$x_{1} = x_{01} + v_{1} \cdot t = v_{1} \cdot t$ .

Теперь найдём закон движения точки А вагона в системе отсчёта, связанной с Землёй. Начальная координата данной точки равна x₀₂ = 0. Точка А движется относительно Земли с постоянной скоростью ${\vec{v}}_{2}$ , сонаправленной с осью ОХ — проекция её скорости на данную ось также будет положительна. К моменту времени t точка сместится вдоль оси ОХ на расстояние $∆ x_{2} = v_{2} \cdot t$ . Закон движения точки А относительно неподвижной системы отсчёта будет иметь следующий вид:

$x_{2} = x_{02} + v_{2} \cdot t = v_{2} \cdot t$ .

Наконец, найдём закон движения человека относительно Земли. Начальная координата человека равна x₀ = 0. Через время t человек сместится на величину Δx, равную

$∆ x = {∆ x}_{1} + {∆ x}_{2}$ .

Тогда с учётом выражений выше закон движения человека относительно Земли имеет следующий вид:

$x = x_{0} + ∆ x = {∆ x}_{1} + {∆ x}_{2} = v_{1} \cdot t + v_{2} \cdot t = (v_{1} + v_{2}) \cdot t$ .

Также можно записать в следующем виде:

$x = v \cdot t$ , где $v = v_{1} + v_{2}$ .

Данное выражение показывает, что человек движется относительно Земли равномерно прямолинейно со скоростью $\vec{v}$ , равной сумме скорости человека относительно вагона ${\vec{v}}_{1}$ и скорости вагона относительно Земли ${\vec{v}}_{2}$ .

Движение человека в поезде относительно Земли есть сумма движения человека относительно поезда и движения поезда относительно Земли.

Задача об относительном движении двух тел

Пусть автомобиль 1 движется со скоростью ${\vec{v}}_{1}$ , автомобиль 2 — со скоростью ${\vec{v}}_{2}$ относительно Земли. Скорости автомобилей относительно неподвижной системы отсчёта направлены так, как показано на рисунке 4. Необходимо найти скорость второго автомобиля относительно первого ${\vec{v}}_{21}$ .

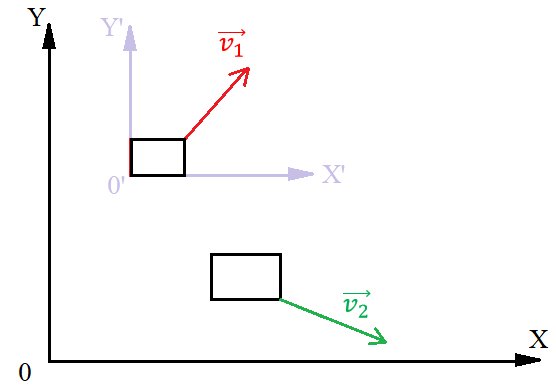Рис. 4. Относительное движение двух тел

Примем, что автомобили являются точечными телами. Движущуюся систему отсчёта X’Y’ свяжем с первым автомобилем. Лабораторную систему отсчёта XY свяжем с Землёй.

Согласно закону сложения скоростей, вектор скорости тела относительно неподвижной системы ${\vec{v}}_{2}$ отсчёта равен сумме вектора скорости данного тела в подвижной системе отсчёта ${\vec{v}}_{21}$ и вектора скорости подвижной системы отсчёта ${\vec{v}}_{1}$ (рис. 5).

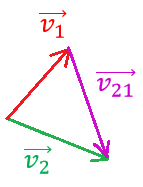Рис. 5. Закон сложения скоростей

${\vec{v}}_{2} = {\vec{v}}_{21} + {\vec{v}}_{1}$ .

Следовательно, скорость второго автомобиля относительно первого равна

${\vec{v}}_{21} = {\vec{v}}_{2} - {\vec{v}}_{1}$ .

Заметим, что скорость первого автомобиля относительно второго ${\vec{v}}_{12}$ можно найти аналогичным образом. Для этого необходимо принять второй автомобиль за подвижную систему отсчёта. Тогда, если скорости первого и второго автомобиля относительно Земли равны ${\vec{v}}_{1}$ и ${\vec{v}}_{2}$ соответственно, скорость первого автомобиля относительно второго находится по следующей формуле:

${\vec{v}}_{12} = {\vec{v}}_{1} - {\vec{v}}_{2}$ .

Модули относительных скоростей ${\vec{v}}_{21}$ и ${\vec{v}}_{12}$ равны.

Физический смысл скоростей ${\vec{v}}_{21}$ и ${\vec{v}}_{12}$ становится очевиден, если представить, что автомобили двигались прямолинейно навстречу друг другу: в этом случае относительная скорость покажет скорость сближения рассматриваемых тел.

Пример 1

Турист на катере переплывает через реку. При этом скорость катера относительно воды перпендикулярна скорости течения и равна 4 м/с. Расстояние между берегами реки 120 м, а скорость течения 3 м/с. За какое время турист переплывёт реку? Чему равен модуль перемещения катера относительно берега за время переправы?

Решение

Рис. 6. К примеру 1

1. Пусть катер движется со скоростью $\vec{v_{к}}$ относительно воды, а скорость течения относительно берега равна $\vec{v_{в}}$ . Расстояние между берегами равно $L$ (см. рис. 6).

2. Движущуюся систему отсчёта $X ’ Y ’$ свяжем с водой. Лабораторную систему отсчёта $X Y$ свяжем с берегом.

3. Из условия скорость катера относительно воды перпендикулярна скорости течения, поэтому можно сразу найти время переправы:

$t = \frac{L}{v_{к}} = \frac{120}{4} = 30 с$ .

4. Чтобы определить модуль перемещения $S$ , необходимо найти общую скорость катера относительно берега. Для этого воспользуемся законом сложения скоростей: $\vec{v} = \vec{v_{к}} + \vec{v_{в}}$ .

По теореме Пифагора определим модуль скорости:

$v = \sqrt{v_{к}^{2} + v_{в}^{2}} = 5 \frac{м}{с}$ .

$⟹ S = v \cdot t = 5 \cdot 30 = 150 м$ .

Ответ: $t = 30 с$ ; $S = 150 м$ .

Упражнение 1

1. Самолёт при попутном ветре преодолевает расстояние $S$ за 90 мин. В случае, когда самолёт летит обратно, скорость и направление ветра остаются такими же, но перелёт длится 110 мин. Скорость самолёта относительно воздуха была постоянной и равна $v_{с}$ . Сколько занял бы перелёт при отсутствии ветра?

Итоги

Вектор скорости тела относительно неподвижной системы отсчёта $\vec{v}$ равен сумме вектора скорости данного тела в подвижной системе отсчёта $\vec{v_{1}}$ и вектора скорости подвижной системы отсчёта $\vec{v_{2}}$ : $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$ .
Перемещение тела относительно неподвижной системы отсчёта $∆ \vec{r}$ равно сумме вектора перемещения данного тела в подвижной системе отсчёта $∆ \vec{r_{1}}$ и вектора перемещения подвижной системы отсчёта $∆ \vec{r_{2}}$ :
$∆ \vec{r} = ∆ \vec{r_{1}} + ∆ \vec{r_{2}}$ .

Контрольные вопросы

1. Сформулируйте правило сложения скоростей при относительном движении.
2. Сформулируйте правило сложения перемещений при относительном движении.
3. Как найти скорость сближения двух тел, движущихся прямолинейно навстречу друг другу?

Ответы

Упражнение 1

1. 99 мин = 1 ч 39 мин

Сложение движений. Преобразования Галилея

План урока

Относительность движения. Сложение движений. Преобразования Галилея
Законы движения тела в разных системах отсчёта
Задача об относительном движении двух тел

Цели урока

знать правила сложения скоростей и перемещений
уметь применять правила сложения скоростей и перемещений при решении задач

Разминка

Как найти перемещение человека, идущего по вагону движущегося поезда?
Как изменится ваша скорость относительно платформы метро, если попытаться идти вверх по эскалатору, движущемуся вниз?
Как найти скорость сближения двух тел?

Относительность движения. Сложение движений. Преобразования Галилея

Скорость, перемещение и законы движения тела зависят от выбора системы отсчёта.

Поясним сказанное на конкретном примере.

Рис. 1. Движение лодки в подвижной воде

Пусть человек на лодке переплывает реку, в которой есть течение, скорость которого равна

v_{2}

. Скорость лодки относительно воды равна

v_{1}

(рис. 1).

1 и Δr₂" loading="lazy" /> Рис. 2. Перемещение человека относительно берега Δr есть сумма векторов Δr₁ и Δr₂

$∆ \vec{r} = {∆ \vec{r}}_{1} + {∆ \vec{r}}_{2}$ .

Разделим обе части уравнения на достаточно малый промежуток времени Δt:

$\frac{∆ \vec{r}}{∆ t} = \frac{{∆ \vec{r}}_{1}}{∆ t} + \frac{{∆ \vec{r}}_{2}}{∆ t}$ .

$\vec{v} = {\vec{v}}_{1} + {\vec{v}}_{2}$ ,

Выражения выше называются преобразованиями Галилея.

Закон сложения скоростей: вектор скорости тела относительно неподвижной системы отсчёта

\vec{v}

равен сумме вектора скорости данного тела в подвижной системе отсчёта

{\vec{v}}_{1}

и вектора скорости подвижной системы отсчёта

{\vec{v}}_{2}

\vec{v} = {\vec{v}}_{1} + {\vec{v}}_{2}

$∆ x = ∆ x_{1} + ∆ x_{2}$ , $∆ y = ∆ y_{1} + ∆ y_{2}$ ;

$v_{x} = v_{1 x} + v_{2 x}$ , $v_{y} = v_{1 y} + v_{2 y}$ .

Законы движения тела в разных системах отсчёта

Рис. 3. Сложение движений человека относительно поезда и поезда относительно Земли

$x_{1} = x_{01} + v_{1} \cdot t = v_{1} \cdot t$ .

$x_{2} = x_{02} + v_{2} \cdot t = v_{2} \cdot t$ .

$∆ x = {∆ x}_{1} + {∆ x}_{2}$ .

Тогда с учётом выражений выше закон движения человека относительно Земли имеет следующий вид:

$x = x_{0} + ∆ x = {∆ x}_{1} + {∆ x}_{2} = v_{1} \cdot t + v_{2} \cdot t = (v_{1} + v_{2}) \cdot t$ .

Также можно записать в следующем виде:

$x = v \cdot t$ , где $v = v_{1} + v_{2}$ .

Задача об относительном движении двух тел

Рис. 4. Относительное движение двух тел

Рис. 5. Закон сложения скоростей

${\vec{v}}_{2} = {\vec{v}}_{21} + {\vec{v}}_{1}$ .

Следовательно, скорость второго автомобиля относительно первого равна

${\vec{v}}_{21} = {\vec{v}}_{2} - {\vec{v}}_{1}$ .

${\vec{v}}_{12} = {\vec{v}}_{1} - {\vec{v}}_{2}$ .

Модули относительных скоростей ${\vec{v}}_{21}$ и ${\vec{v}}_{12}$ равны.

Пример 1

Решение

Рис. 6. К примеру 1

2. Движущуюся систему отсчёта $X ’ Y ’$ свяжем с водой. Лабораторную систему отсчёта $X Y$ свяжем с берегом.

$t = \frac{L}{v_{к}} = \frac{120}{4} = 30 с$ .

По теореме Пифагора определим модуль скорости:

$v = \sqrt{v_{к}^{2} + v_{в}^{2}} = 5 \frac{м}{с}$ .

$⟹ S = v \cdot t = 5 \cdot 30 = 150 м$ .

Ответ: $t = 30 с$ ; $S = 150 м$ .

Упражнение 1

Итоги

Вектор скорости тела относительно неподвижной системы отсчёта $\vec{v}$ равен сумме вектора скорости данного тела в подвижной системе отсчёта $\vec{v_{1}}$ и вектора скорости подвижной системы отсчёта $\vec{v_{2}}$ : $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$ .
Перемещение тела относительно неподвижной системы отсчёта $∆ \vec{r}$ равно сумме вектора перемещения данного тела в подвижной системе отсчёта $∆ \vec{r_{1}}$ и вектора перемещения подвижной системы отсчёта $∆ \vec{r_{2}}$ :
$∆ \vec{r} = ∆ \vec{r_{1}} + ∆ \vec{r_{2}}$ .

Контрольные вопросы

Ответы

Упражнение 1

1. 99 мин = 1 ч 39 мин

Конспект урока: Сложение движений. Преобразования Галилея

Кинематика

Относительность движения. Сложение движений. Преобразования Галилея

Законы движения тела в разных системах отсчёта

Задача об относительном движении двух тел

Относительность движения. Сложение движений. Преобразования Галилея

Законы движения тела в разных системах отсчёта

Задача об относительном движении двух тел